时间:2017-08-05 17:42:30
1、计算题 如图所示,在xoy坐标系中,以(r,0)为圆心、r为半径的圆形区域内存在匀强磁场,磁场的磁感应强度大小为B,方向垂直于纸面向里。在y>r的足够大的区域内,存在沿y轴负方向的匀强电场,场强大小为E。从O点以相同速率向不同方向发射质子,质子的运动轨迹均在纸面内,且质子在磁场中运动的轨迹半径也为r。已知质子的电荷量为q,质量为m,不计质子所受重力及质子间相互作用力的影响。
(1)求质子射入磁场时速度的大小;
(2)若质子沿x轴正方向射入磁场,求质子从O点进入磁场到第二次离开磁场经历的时间;
(3)若质子沿与x轴正方向成夹角θ的方向从O点射入第一象限的磁场中,求质子在磁场中运动的总时间。 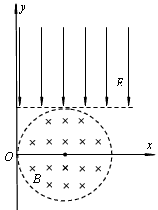
参考答案:解:(1)质子射入磁场后做匀速圆周运动,有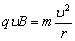
得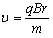
(2)质子沿x轴正向射入磁场后,在磁场中运动了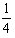 个圆周后,以速度υ逆着电场方向进入电场,原路径返回后,再射入磁场,在磁场中运动了
个圆周后,以速度υ逆着电场方向进入电场,原路径返回后,再射入磁场,在磁场中运动了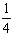 个圆周后离开磁场
个圆周后离开磁场
在磁场中运动周期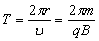
质子在磁场中运动的时间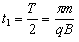
进入电场后做匀变速直线运动,加速度大小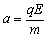
质子在电场中运动的时间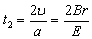
所求时间为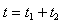 =
=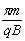 +
+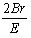
(3)当质子沿与x轴正方向成夹角θ的方向从第一象限射入磁场时,设质子将从A点射出磁场,如图所示,其中O1、O2分别为磁场区域圆和质子轨迹圆的圆心。由于轨迹圆的半径等于磁场区域圆的半径,所以OO1AO2为菱形,即AO2平行x轴,说明质子以平行y轴的速度离开磁场,也以沿y轴负方向的速度再次进入磁场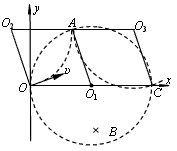
∠O2=90°-θ,所以,质子第一次在磁场中运动的时间t1′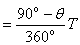
此后质子轨迹圆的半径依然等于磁场区域圆的半径,设质子将从C点再次射出磁场,如图所示,其中O1、O3分别为磁场区域圆和质子轨迹圆的圆心,AO3平行x轴。由于O1AO3C为菱形,即CO1平行AO3,即平行x轴,说明C就是磁场区域圆与x轴的交点。这个结论与θ无关
所以,O O2O3C为平行四边形,∠O3=90°+θ
质子第二次在磁场中运动的时间t2′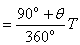
质子在磁场中运动的总时间t′=t1′+t2′=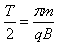
本题解析:
本题难度:困难
2、实验题 如图所示,匀强电场方向向右,匀强磁场方向垂直于纸面向里,一质量为m、带电荷量为q的微粒以速度v与磁场方向垂直、与电场方向成45°角射入复合场中,恰能做匀速直线运动.则电场强度E=______________,磁感应强度B=______________.
参考答案: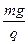 ?
?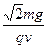
本题解析:进行正确的受力分析,由共点力平衡知识可求得E=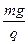 ,B=
,B=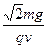 .
.
本题难度:一般
3、计算题 如图所示,在半径为R的绝缘圆筒内有匀强磁场,方向垂直于纸面向里,圆筒正下方有小孔C与平行金属板M、N相通。两板间距离为d,两板与电动势为E的电源连接。一电荷量为-q、质量为m的带电粒子(重力忽略不计),开始时静止于C点正下方紧靠N板的A点,经电场加速后从C点进入磁场,并以最短的时间从C 点射出。已知带电粒子与筒壁的碰撞无电荷量的损失,且碰撞后以原速率返回,求:
(1)筒内磁场的磁感应强度大小;
(2)带电粒子从A点出发至第一次回到A点所经历的时间。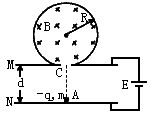
参考答案:解:(1)如图所示,带电粒子从C孔进入,与筒壁碰撞两次再从C孔射出经历的时间最短,设粒子在磁场中做匀速圆周运动的速率为v,有: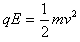
得:v=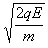
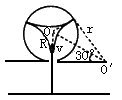
由几何关系可知,粒子在磁场中的运动半径为:r=Rcot30°
粒子在磁场中运动时有:qvB=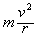
解得:B=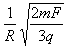
(2)粒子从A到C运动时的加速度为: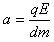
由d=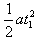 得,粒子从A到C的时间为:t1=
得,粒子从A到C的时间为:t1=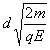
粒子在磁场中运动的时间为: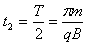
解得:t2=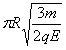
因此带电粒子从A点出发至第一次回到A点的时间为:t=2t1+t2=(2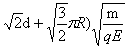
本题解析:
本题难度:困难
4、选择题 如图所示的电路中,三个灯泡L1、L2、L3的电阻关系为R1<R2<R3,电感L的电阻可忽略,D为理想二极管。电键K从闭合状态突然断开时,下列判断中不正确的是(?)
A.L1逐渐变暗
B.L1先变亮,然后逐渐变暗
C.L3先变亮,然后逐渐变暗
D.L2立即熄灭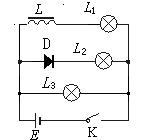
参考答案:B
本题解析:K处于闭合状态时,电感L和二极管均相当于导线,通过灯泡L1、L2、L3的电流关系为I1>I2>I3。当K突然断开时,电感L相当于电源,由此时二极管处于反向截止状态,故L2立即熄灭,D正确;L、L1和L3构成一闭合回路,L中电流从I1逐渐减少,则通过L1的电流也逐渐减少,选项A正确,B错误。通过L3的电流开始时比原来电流大,后逐渐变小,故选项C正确。
本题难度:简单
5、计算题 (10分)?如图所示,电动机带着绷紧的传送带始终以v0=2 m/s的速度运动,传送带与水平面的夹角θ=30°,现把一质量为m=10kg的工件轻轻地放在皮带的底端,经过一段时间后,工件送到高h=2m的平台上,已知工件与皮带之间的动摩擦因数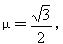 除此之外,不记其他损耗。求电动机由于传送工件多消耗的电能。(取g=10 m/s2)
除此之外,不记其他损耗。求电动机由于传送工件多消耗的电能。(取g=10 m/s2)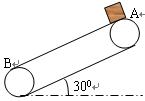
参考答案:280 J
本题解析:作出工件在传送带上受力如图所示,f为皮带给予工件的滑动摩擦力,对工件, 根据牛顿第二定律,有:
μmgcosθ-mg sinθ=ma?代入数据解得:? a=2.5 m/s2(2分)?工件达到传送带运转速度v0=2 m/s时所用的时间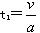 ?代入数据解得:? t1=0.8s
?代入数据解得:? t1=0.8s
工件在传送带上加速运动的距离为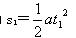 ?代入数据解得:? s1=0.8 m(2分)?
?代入数据解得:? s1=0.8 m(2分)?
故有:? s1<h/ sin30°?
说明工件在传送带上现做匀加速运动,再做匀速运动,工件到达平台时的速度为2 m/s .
故工件增加的机械能E=mgh+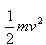 ?代入数据得E=220 J?(2分),
?代入数据得E=220 J?(2分),
设在t1时间内传送带的位移为s2,故转化的内能为:? W=f (s2-s1)=fs1?
代入数据得W=60J?(2分)
电动机由于传送工件多消耗的电能。△E=E+W=280 J?(2分)
本题难度:一般