时间:2017-08-05 17:42:30
1、计算题 （20分）一个“
”形导轨PONQ，其质量为M=2.0kg，放在光滑绝缘的水平面上，处于匀强磁场中，另有一根质量为m=0.60kg的金属棒CD跨放在导轨上，CD与导轨的动摩擦因数是0.20，CD棒与ON边平行，左边靠着光滑的固定立柱a、b，匀强磁场以ab为界，左侧的磁场方向竖直向上（图中表示为垂直于纸面向外），右侧磁场方向水平向右，磁感应强度的大小都是0.80T，如图所示，已知导轨ON段长为0.50m，电阻是0.40Ω，金属棒CD的电阻是0.20Ω，其余电阻不计。导轨在水平拉力作用下由静止开始以0.20m/s2的加速度做匀加速直线运动，一直到CD中的电流达到4.0A时，导轨改做匀速直线运动.设导轨足够长，取g=10m/s2.求：
⑴导轨运动起来后，C、D两点哪点电势较高？
⑵导轨做匀速运动时，水平拉力F的大小是多少？
⑶导轨做匀加速运动的过程中，水平拉力F的最小值是多少？
⑷CD上消耗的电功率为P=0.80W时，水平拉力F做功的功率是多大？
参考答案：（1）C；（2）2.48N；（3）1.6N；（4）6.72W。
本题解析：（1）当导轨运动起来后，ON向左做切割磁感线的运动，由右手定则可判断出感应电流的方向由N到O，则对于CD来说，流过它的电流是由C到D，故C点的电势高于D点；
（2）由于导轨做匀速直线运动时，CD中的电流为4A，则导轨受到的安培力F=BIL=0.8T×4A×0.5m=1.6N，方向与拉力的方向相反；
另外导轨还受到向右的摩擦力，由于此时导体棒受到的安培力为F1= BIL=0.8T×4A×0.5m=1.6N，
导体棒对导轨的压力大小为mg－F1=0.6kg×10N/kg－1.6N=4.4N，
故导体棒受到的摩擦力的大小为f=4.4N×0.2=0.88N，
由于导轨处于匀速直线运动状态，故其受到的力平衡，则F=1.6N+0.88N=2.48N。
（3）设当导轨的速度为v时，水平拉力F′的值最小，故此时的ON受到的安培力大小等于CD受到的安培力大小，即
FON=BL×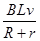
=
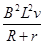，方向向右；
则CD棒受到的摩擦力的大小为f=(mg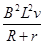－)μ，
由牛顿第二定律可得：F′－FON－f=Ma，
故F′=Ma+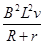+(mg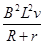－)μ=Ma+mgμ+(1－μ)×，
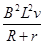故当v=0时水平拉力F′的值最小，即F′=Ma+mgμ=2kg×0.2m/s2+0.6kg×10N/kg×0.2=1.6N。
（4）当CD上消耗的电功率为P=0.80W时，
根据电功率的计算公式可计算出导体棒上的电流I′=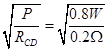
=2A，
设导轨的速度为v′，则由感应电动势和欧姆定律得EON=I′（R+r）=BLv′
故v′=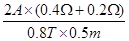
=3m/s；
设此时的拉力为F拉，
则安培力的大小为F安=0.8T×0.5m×2A=0.8N，摩擦力的大小为（6N－0.8N）×0.2=1.04N，
由牛顿第二定律可得F拉－0.8N－1.04N=Ma=0.4N，故F拉=2.24N，
所以拉力的功率为P=F拉v′=2.24N×3m/s=6.72W。
本题难度：一般
2、选择题 如图所示，平行板电容器的两板与电源相连，板间同时有电场和垂直纸面向里的匀强磁场B，一个带电荷量为+q的粒子以v0为初速度从两板中间沿垂直电磁场方向进入，穿出时粒子的动能减小了，若想使这个带电粒子以v0沿原方向匀速直线运动穿过电磁场，可采用的办法是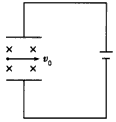 
[? ]
A．减小平行板的正对面积
B．增大电源电压
C．减小磁感应强度B
D．增大磁感应强度B
参考答案：BC
本题解析：
本题难度：一般
3、计算题 如图所示，等腰直角三角形ABC区域内有磁感应强度大小为B，方向垂直纸面匈里的匀强磁场，AB边水平。磁场下方有一方向水平向右的匀强电场。现有一质量为m电量为q的负离子（重力不计），以速度v0沿图中虚线垂直电场且正对三角形ABC的顶点C射入，穿过电场区域后，负离子从AB边进入磁场，又从AB边射出。已知AB=
，电场宽度L=
。求：
（1）负离子在AB边上入射点与出射点的距离；
（2）保持电场宽度L不变，调整电场上边界与磁场边界AB间的距离及电场强度的大小，使负离子在磁场中运动的时间最长，则此时电场强度E多大？
参考答案：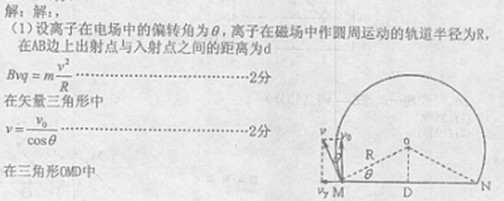
本题解析：略
本题难度：一般
4、计算题 （20分）电视机的显像管中，电子束的偏转是用电偏和磁偏转技术实现的。如图甲所示，电子枪发射出的电子经小孔S1进入竖直放置的平行金属板M、N间，两板间所加电压为U0；经电场加速后，电子由小孔S2沿水平放置金属板P和Q的中心线射入，两板间距离和长度均为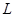
；距金属板P和Q右边缘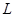处有一竖直放置的荧光屏；取屏上与S1、S2共线的O点为原点，向上为正方向建立x轴。已知电子的质量为m，电荷量为e，初速度可以忽略。不计电子重力和电子之间的相互作用。
（1）求电子到达小孔S2时的速度大小v；
（2）若金属板P、Q间只存在垂直于纸面向外的匀强磁场，电子恰好经过P板的右边缘飞出，求磁场的磁感应强度大小B；
（3）若金属板P和Q间只存在电场，P、Q两板间电压u随时间t的变化关系如图乙所示，单位时间内从小孔S1进入的电子个数为N。电子打在荧光屏上形成一条亮线；每个电子在板P和Q间运动的时间极短，可以认为两板间的电压恒定；忽略电场变化产生的磁场。试求在一个周期（即2t0时间）内打到荧光屏单位长度亮线上的电子个数n。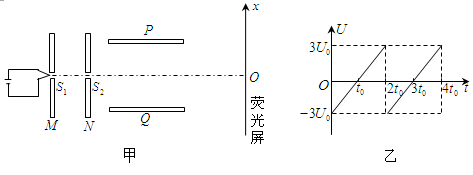
参考答案：（1）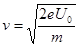
?（2）
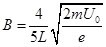?（3）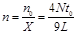
本题解析：（1）根据动能定理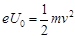
?①
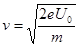解得：?②
（2）电子在磁场中做匀速圆周运动，设圆运动半径为 R，在磁场中运动轨迹如图，由几何关系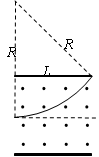
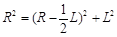?③
根据牛顿第二定律：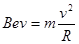
?④?
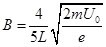解得：?⑤?
（3） 设电子在偏转电场PQ中的运动时间为t，PQ间的电压为u时恰好打在极板边缘
垂直电场方向：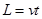
?⑥
平行电场方向：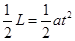
?⑦
此过程中电子的加速度大小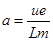 
?⑧
解得：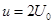
， 即当两板间电压为
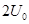时打在极板上?⑨
电子出偏转电场时，在x方向的速度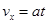
?⑩
电子在偏转电场外做匀速直线运动，设经时间t2到达荧光屏。则
水平方向：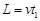
?
竖直方向：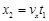
?
电子打在荧光屏上的位置坐标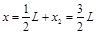
?
亮线长度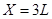
?
一个周期内打在荧光屏上的电子数：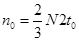
?
2t0时间内，打到单位长度亮线上的电子个数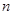
：?
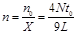评分标准：①③④⑤式各2分，其余各式均1分，共计20分。
本题难度：一般
5、选择题 如图所示，两平行金属板中有相互垂直的匀强电场和匀强磁场，带正电的粒子（不计粒子的重力）从两板中央垂直电场、磁场入射．它在金属板间运动的轨迹为水平直线，如图中虚线所示．若使粒子飞越金属板间的过程中向上板偏移，则可以采取下列的正确措施为（ ）
A．使入射速度增大
B．使粒子电量增大
C．使电场强度增大
D．使磁感应强度增大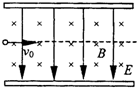
参考答案：由题，带正电的粒子进入两板中央，受到竖直向下的电场力和竖直向上的洛伦兹力，开始时粒子的轨迹为水平直线，则电场力与洛伦兹力平衡，即有 qvB=qE，即vB=E，
若使粒子飞越金属板间的过程中向上板偏移，洛伦兹力必须大于电场力，则qvB＞qE，即vB＞E．
A、使入射速度增大，洛伦兹力增大，而电场力不变，则粒子向上偏转．故A正确．
B、由上式可知，改变电量，电场力与洛伦兹力仍然平衡，粒子仍沿水平直线运动．故B错误．
C、使电场强度增大，电场力增大，粒子向下偏转．故C错误．
D、使磁感应强度增大，洛伦兹力增大，则粒子向上偏转．故D正确．
故选AD
本题解析：
本题难度：简单