时间:2017-03-02 10:41:52
1、选择题 如图14所示，虚线框中存在垂直纸面向外的匀强磁场B和平行纸面且与竖直平面夹角为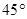
斜向下的匀强电场E，有一质量为m，电荷量为q的带负电的小球在高为h处的P点从静止开始自由下落，当小球运动到复合场内时刚好做直线运动，那么（?）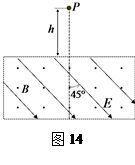
A．小球在复合场中一定做匀速直线运动
B．磁感应强度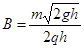
，场强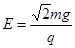
C．若换成带正电的小球，小球仍可能做直线运动
D．若同时改变小球的比荷与初始下落高度h，小球仍能沿直线通过复合场
2、选择题 如图所示，在平行线．MN、PQ之间存在竖直向上的匀强电场和垂直纸面的磁场(未画出)，磁场的磁感应强度从左到右逐渐增大。一带电微粒进入该区域时，由于受到空气阻力作用，恰好能沿水平直线OO’通过该区域。带电微粒所受的重力忽略不计，运动过程带电量不变。下列判断正确的是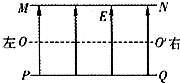
A．微粒从左向右运动，磁场方向向里
B．微粒从左向右运动，磁场方向向外
C．微粒从右向左运动，磁场方向向里
D．微粒从右向左运动，磁场方向向外
3、选择题 如图所示，某空间存在正交的匀强磁场和匀强电场，电场方向水平向右，磁场方向垂直纸面向里，一带电微粒由A点进入电磁场并刚好能沿AB直线向上运动，则该微位在A、B两点的动能Ek和电势能EP的关系是（ ）
A．.EKA＜EKB
B．EKA＞EKB
C．.EPA＜EPB
D．.EPA＞EPB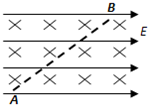
4、计算题 （12分）如下图所示，在xoy直角坐标系中，第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场，第Ⅱ象限内分布着方向沿y轴负方向的匀强电场。初速度为零、带电量为q、质量为m的离子经过电压为U的电场加速后，从x上的A点垂直x轴进入磁场区域，经磁场偏转后过y轴上的P点且垂直y轴进入电场区域，在电场偏转并击中x轴上的C点。已知OA=OC=d。求：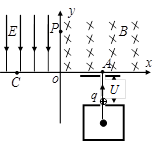
（1）磁感强度B的大小．
（2）电场强度E的大小．
（3）离子从A到C运动的时间．
5、计算题 如图所示，在直角坐标系Oxy平面的第三、四象限内分别存在着垂直于Oxy平面的匀强磁场，第三象限的磁感应强度大小是第四象限的2倍，方向相反。质量、电荷量相同的负粒子a、b，某时刻以大小相同的速度分别从x轴上的P、Q两点沿y轴负方向垂直射入第四、三象限磁场区域。已知a粒子在离开第四象限磁场时，速度方向与y轴的夹角为60o，且a在第四象限磁场中运行时间是b粒子在第三象限磁场中运行时间的4倍。不计重力和两粒子之间的相互作用力。求： a、b两粒子经Y轴时距原点O的距离之比。