时间:2017-03-02 10:41:52
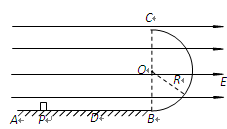
1、计算题 如图所示,水平绝缘粗糙的轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接,半圆形轨道的半径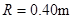 .在轨道所在空间存在水平向右的匀强电场,电场线与轨道所在的平面平行,电场强度
.在轨道所在空间存在水平向右的匀强电场,电场线与轨道所在的平面平行,电场强度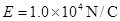 .现有一电荷量
.现有一电荷量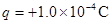 ,质量
,质量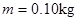 的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体恰好能通过半圆形轨道的最高点C,然后落至水平轨道上的D点.取
的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体恰好能通过半圆形轨道的最高点C,然后落至水平轨道上的D点.取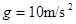 .
.
试求:
(1)带电体在圆形轨道C点的速度大小.
(2)D点到B点的距离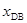 .
.
(3)带电体运动到圆形轨道B点时对圆形轨道的压力大小.
(4)带电体在从P开始运动到落至D点的过程中的最大动能。
参考答案:(1) 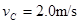 ?(2)
?(2) 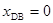 ?(3)
?(3) 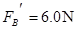 ?(4)
?(4) 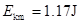
本题解析:(1)设带电体通过C点时的速度为vC,依据牛顿第二定律: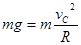 ---------------------------------1分
---------------------------------1分
解得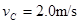 ------------------------------1分
------------------------------1分
(2)设带电体从最高点C落至水平轨道上的D点经历的时间为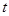 ,根据运动的分解有:
,根据运动的分解有: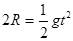 ------------------------------------1分
------------------------------------1分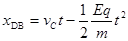 -----------------------------2分
-----------------------------2分
联立解得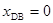 -------------------------------1分
-------------------------------1分
(3)设带电体通过B点时的速度为vB,设轨道对带电体的支持力大小为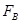 ,带电体在B点时,根据牛顿第二定律有
,带电体在B点时,根据牛顿第二定律有 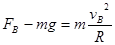 --------1分
--------1分
带电体从B运动到C的过程中,依据动能定理: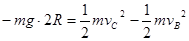 ---------------------------2分
---------------------------2分
联立解得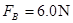 -------------------------------------1分
-------------------------------------1分
根据牛顿第三定律,带电体对轨道的压力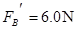 --------------1分
--------------1分
(4)由P到B带电体作加速运动,故最大速度一定出现在从B经C到D的过程中.在此过程中只有重力和电场力做功,这两个力大小相等,其合力与重力方向成45?夹角斜向右下方,故最大速度必出现在B点右侧对应圆心角为45 ?处.
设小球的最大动能为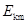 ,根据动能定理有:
,根据动能定理有: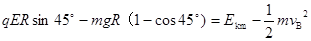 -----------2分
-----------2分
解得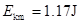 (或
(或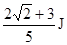 )--------------------1分
)--------------------1分
点评:做此类型的题目,需要根据圆周运动知识分析最高点或者最低点的速度,然后根据能量守恒定律分析解题
本题难度:一般
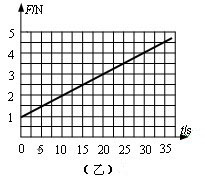
2、计算题 如图(甲)所示,一对平行光滑轨道放置在水平面上,两轨道间距L=0.20 m,电阻R=10 W,有一质量为1kg的导体棒平放在轨道上并与两轨道垂直,导体棒及轨道的电阻皆可忽略不计,整个装置处于垂直轨道平面向下的匀强磁场中。现从t=0开始,用一水平向右的外力F沿轨道方向拉动导体棒,使之做初速度为零的匀加速直线运动,F与时间t的关系如图(乙)所示,试求:
(1)导体棒运动的加速度a。
(2)磁场的磁感应强度B。
(3)导体棒运动到第20s时,电阻R的电功率。
(4)若改为恒定拉力作用,但仍要导体棒以该加速度做匀加速运动,在其它条件不变的
情况下,简要说明磁场的磁感应强度必须满足的条件。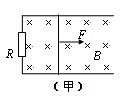
参考答案:(1)1m/s2
(2)5T
(3)40W
(4)磁场随距离变化的关系:B∝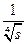
本题解析:(1)F-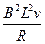 =ma,则a=1m/s2。?(3分)
=ma,则a=1m/s2。?(3分)
(2)B=5T?(4分)
(3)v=a t=20 m/s,则P=(F拉-ma)v=40W。?(4分)
(4)根据F -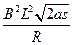 =ma,磁场随距离变化的关系:B∝
=ma,磁场随距离变化的关系:B∝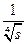 。(3分)
。(3分)
本题难度:一般
3、计算题 (18分)如图a所示,竖直直线MN左方有水平向右的匀强电场,现将一重力不计,比荷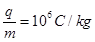 的正电荷置于电场中O点由静止释放,经过
的正电荷置于电场中O点由静止释放,经过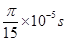 后,电荷以v0=1.5×104m/s的速度通过MN进入其右方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻,忽略磁场变化带来的影响)。求:
后,电荷以v0=1.5×104m/s的速度通过MN进入其右方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻,忽略磁场变化带来的影响)。求: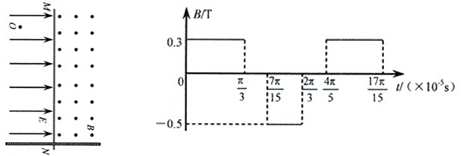
(1)匀强电场的电场强度E;
(2)图b中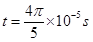 时刻电荷与O点的竖直距离r。
时刻电荷与O点的竖直距离r。
(3)如图在O点下方d=39.5cm处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板所需要的时间。(结果保留2位有效数字)
参考答案:7.2×103N/C? 4cm? 2.1×10-4s
本题解析:(1)电荷在电场中做匀加速直线运动,设其在电场中运动的时间为t1 ,有:
根据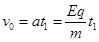
解得: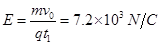
(2)当磁场垂直纸面向外时,电荷运动的半径: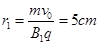
周期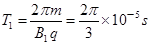
当磁场垂直纸面向里时,电荷的运动半径: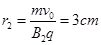 周期:
周期: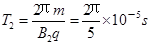
电荷从t=0进入磁场开始做周期性运动,其运动轨迹如图所示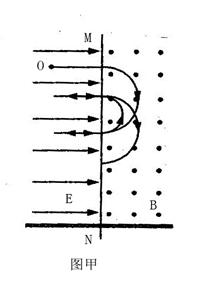
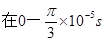 时间内,带电粒子经时间
时间内,带电粒子经时间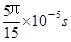 完成半周期圆周运动进入电场,在电场中往返时间为
完成半周期圆周运动进入电场,在电场中往返时间为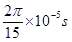 ,再次进入磁场,磁场方向发生变化,经
,再次进入磁场,磁场方向发生变化,经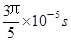 完成半周期圆周运动,再次进入电场,在电场中往返时间为
完成半周期圆周运动,再次进入电场,在电场中往返时间为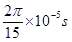 ,距O点的距离为4cm.
,距O点的距离为4cm.
(3)电荷从第一次通过MN开始,其运动的周期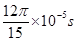 ,
,
根据电荷的运动情况,可知,电荷到达挡板前运动的完整周期数为8个,此时电荷沿MN运动的距离: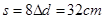 ?
?
则最后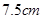 的距离如图乙所示,
的距离如图乙所示, 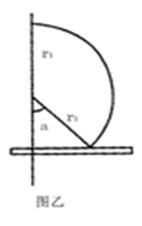
有: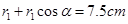
解得: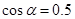 ,则
,则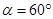 ? (3分)
? (3分)
故电荷运动的总时间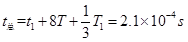 ? (3分)
? (3分)
本题难度:一般
4、计算题 (11分)(2009·安徽省六校联考)如图所示,为某种新型设备内部电、磁场分布情况图.自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域.区域Ⅰ宽度为d1,分布有沿纸面向下的匀强电场E1;区域Ⅱ宽度为d2,分布有垂直纸面向里的匀强磁场B1;宽度可调的区域Ⅲ中分布有沿纸面向下的匀强电场E2和垂直纸面向里的匀强磁场B2.现在有一群质量和带电荷量均不同的带正电粒子从区域Ⅰ上边缘的注入孔A点被注入,从静止开始运动,然后相继进入Ⅱ、Ⅲ两个区域,满足一定条件的粒子将回到区域Ⅰ,其他粒子则从区域Ⅲ飞出.三区域都足够长,粒子的重力不计.
已知能飞回区域Ⅰ的带电粒子的质量为m=6.4×10-27kg,带电荷量为q=3.2×10-19C,且d1=10cm,d2=5cm,d3>10cm,E1=E2=40V/m,B1=4×10-3T,B2=2×10-3T.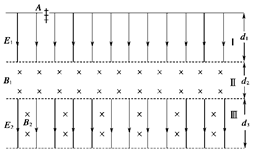
试求:
(1)该带电粒子离开区域Ⅰ时的速度.
(2)该带电粒子离开区域Ⅱ时的速度.
(3)该带电粒子第一次回到区域Ⅰ的上边缘时离开A点的距离.
参考答案:(1)2×104m/s 方向竖直向下
(2)2×104m/s 方向与x轴正向成45°角
(3)57.26cm
本题解析:(1)qE1d1=mv2
得:v=2×104m/s,方向竖直向下.
(2)速度大小仍为v=2×104m/s,如图所示.
qB1v=m
方向:sinθ=
可得:θ=45°
所以带电粒子离开区域Ⅱ时的速度方向与x轴正向成45°角.
(3)设该带电粒子离开区域Ⅱ也即进入区域Ⅲ时的速度分解为vx、vy,则:vx=vy=vsin45°=×104m/s
所以:qB2vx=qB2vy=1.28×10-17N.
qE2=1.28×10-17N
qE2=qB2vx
所以带电粒子在区域Ⅲ中运动可视为沿x轴正向的速率为vx的匀速直线运动和以速率为vy,以及对应洛伦兹力qB2vy作为向心力的匀速圆周运动的叠加,轨道如图所示: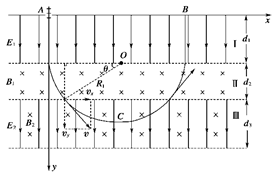
R2==10cm
T==π×10-5s
根据运动的对称性可知,带电粒子回到区域Ⅰ的上边缘的B点,距A点的距离为:d=2
代入数据可得:d≈57.26cm
本题难度:一般
5、选择题 如图所示,带负电的液滴以速度v垂直射入方向一致的水平匀强磁场和匀强电场区域,则液滴可能做(?)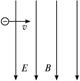
A.匀速直线运动
B.匀变速直线运动
C.匀变速曲线运动
D.匀速圆周运动
参考答案:C
本题解析:此题极易错选为D,原因是将场区当成竖直向下的,未看清题目中同向场区是水平的.显然A、B、D不可能.当mg=qvB时,带电粒子受合外力为qE.且初速v与qE互相垂直,在初速v方向液滴做匀速直线运动,在电场力qE方向做初速为零的匀加速直线运动(此方向分速度与磁场方向平行,不会引起液滴所受洛伦兹力的变化).
故液滴虽然速率增大,但合外力仍然恒定,所以液滴是可能做匀变速曲线运动的,正确选项为C.
本题难度:简单