时间:2016-03-05 16:46:38
2006年考研数学（二）真题及答案详解
一、填空题
（1）曲线
的水平渐近线方程为 .
（2）设函数
在
处连续，则
.
（3）广义积分
.
（4）微分方程
的通解是 .
（5）设函数
由方程
确定，则
= .
（6）设矩阵
，
为2阶单位矩阵，矩阵
满足
，则
=
.
二、选择题
（7）设函数
具有二阶导数，且
，
为自变量
在
处的增量，
与
分别为
在点处对应的增量与微分，若
，则
（A）
（B）
（C）
（D）
【 】
（8）设是奇函数，除外处处连续，是其第一类间断点，则
是
（A）连续的奇函数. （B）连续的偶函数
（C）在间断的奇函数 （D）在间断的偶函数. 【 】
（9）设函数
可微，
，则
等于
（A）
. （B）
（C）
（D）
【 】
（10）函数
满足一个微分方程是
（A）
（B）
（C）
（D）
（11）设
为连续函数，则
等于
（A）
（B）
（C）
（D）
【 】
（12）设与
均为可微函数，且
. 已知
是在约束条件
下的一个极值点，下列选项正确的是
（A）若
，则
.
（B）若，则
.
（C）若
，则.
（D）若，则. 【 】
（13）设
均为
维列向量，
是
矩阵，下列选项正确的是
（A）若线性相关，则
线性相关.
（B）若线性相关，则线性无关.
（C）若线性无关，则线性相关.
（D）若线性无关，则线性无关. 【 】
（14）设为3阶矩阵，将的第2行加到第1行得，再将的第1列的-1倍加到第2列得
，记
，则
（A）
（B）
（C）
（D）
三 解答题
15．试确定A，B，C的常数值，使得
，其中
是当
.
16．
.
17．
，
18．
；
.
19．
20 设函数
满足等式
.
(Ⅰ)验证
；(Ⅱ)若
.
21 已知曲线
的方程为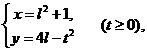
（Ⅰ）讨论的凹凸性；
（Ⅱ）过点（-1，0）引的切线，求切点，并写出切线的方程；
（Ⅲ）求此切线与（对应于
的部分）及轴所围成的平面图形的面积.
22 已知非齐次线性方程组
Ⅰ证明方程组系数矩阵A的秩
；
Ⅱ求
的值及方程组的通解.
23 设3阶实对称矩阵A的各行元素之和均为3,向量
是线性方程组A=0的两个解, (Ⅰ)求A的特征值与特征向量 (Ⅱ)求正交矩阵Q和对角矩阵A,使得
.
一、填空题
（1）曲线的水平渐近线方程为
（2）设函数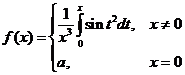
在x=0处连续，则a=
（3）广义积分
（4）微分方程的通解是
（5）设函数
确定，则
当x=0时，y=1，
又把方程每一项对x求导，
(6) 设A = 2 1 ,2阶矩阵B 满足BA=B +2E,则|B|= .
-1 2
解:由BA=B +2E化得B(A-E)=2E,两边取行列式,得
|B||A-E|=|