时间:2017-08-08 07:47:15
1、选择题 如图所示,虚线框abcd内为一矩形匀强磁场区域,ab=2bc,磁场方向垂直于纸面;实线框a′b′c′d′是一正方形导线框,a′b′边与ab边平行.若将导线框匀速地拉离磁场区域,以W1表示沿平行于ab的方向拉出过程中外力所做的功,W2表示以同样速率沿平行于bc的方向拉出过程中外力所做的功,则( )
A.W1=W2
B.W2=2W1
C.W1=2W2
D.W2=4W1
参考答案:B
本题解析:
本题难度:简单
2、简答题 如图甲所示,两根足够长的平行金属导轨MN、PQ相距为L,导轨平面与水平面夹角为α,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m,导轨处于匀强磁场中,磁场的方向垂直于导轨平面斜向上,磁感应强度大小为B,金属导轨的上端与开关S、定值电阻R1和电阻箱R2相连.不计一切摩擦,不计导轨、金属棒的电阻,重力加速度为g,现闭合开关S,将金属棒由静止释放.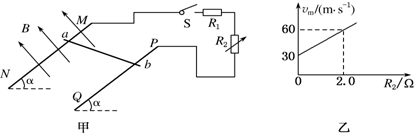
(1)判断金属棒ab中电流的方向;
(2)若电阻箱R2接入电路的阻值为R2=2R1,当金属棒下降高度为h时,速度为v,求此过程中定值电阻R1上产生的焦耳热Q1;
(3)当B=0.40T、L=0.50m、α=37°时,金属棒能达到的最大速度vm随电阻箱R2阻值的变化关系如图乙所示.取g=10m/s2,sin37°=0.60,cos37°=0.80.求定值电阻的阻值R1和金属棒的质量m.
参考答案:(1)由右手定则,金属棒ab中的电流方向为b到a.
(2)由能量守恒定律得:mgh=12mv2+Q,解得:Q=mgh-12mv2,
两电阻串联,通过它们的电流相等,且R2=2R1,则Q1Q2=R1R2=12,
Q1+Q2=Q,则Q1=13Q=13mgh-16mv2;
(3)设最大速度为v,切割磁感线产生的感应电动势:E=BLv
由闭合电路的欧姆定律:I=ER1+R2,
从b端向a端看,金属棒受力如图:
金属棒达到最大速度时满足:
mgsinα-BIL=0
由以上三式得:v=mgsinαB2L2(R1+R2),
由图象可知:斜率为:k=60-302=15m/s?Ω,纵截距为v0=30m/s,
得到:v0=mgsinαB2L2R1,k=mgsinB2L2,
解得:R1=2.0Ω,m=0.1kg.
答:(1)金属棒ab中的电流方向为b到a.
(2)定值电阻R1上产生的焦耳热Q1=13mgh-16mv2;
(3)定值电阻的阻值R1=2.0Ω,金属棒的质量m=0.1kg.
本题解析:
本题难度:一般
3、填空题 如图所示,两根光滑的金属导轨MN、M′N′平行固定于同一水平面内,导轨间距为l=0.50m,电阻不计.M、M′间接有阻值R=1.6Ω的电阻.金属棒ab垂直于导轨放置.导轨处于磁感应强度B=0.20T、方向竖直向下的匀强磁场中.金属棒ab在外力作用下向右匀速运动,速度v=10m/s,运动过程中金属棒ab与导轨保持良好接触.已知金属棒ab接入电路部分的阻值r=0.40Ω.求:
(1)金属棒ab中电流I的大小和方向;
(2)1min内电阻R上产生的热量Q.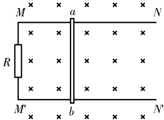
参考答案:(1)设金属棒ab切割磁感线产生的感应电动势为E,根据法拉第电磁感应定律、闭合电路欧姆定律:
ab棒产生的感应电动势为:E=Blv=0.20×0.50×10V=1V,
电路中感应电流为:I=ER+r
解得:I=11.6+0.4A=0.50A
根据右手定则:电流方向b→a
(2)设1min电阻R上产生的热量为Q,根据焦耳定律:Q=I2Rt=24J
答:(1)金属棒ab中电流I的大小为0.50A,电流方向b→a;
(2)1min内电阻R上产生的热量Q为24J.
本题解析:
本题难度:一般
4、简答题 如图1所示,光滑矩形斜面ABCD的倾角θ=30°,在其上放置一矩形金属线框abcd,ab的边长l1=1m,bc的边长l2=0.6m,线框的质量m=1kg,电阻R=0.1Ω,线框通过细线绕过定滑轮与重物相连,细线与斜面平行且靠近;重物质量M=2kg,离地面的高度为H=4.8m;斜面上efgh区域是有界匀强磁场,磁感应强度的大小为0.5T,方向垂直于斜面向上;已知AB到ef的距离为4.2m,ef到gh的距离为0.6m,gh到CD的距离为3.2m,取g=10m/s2;现让线框从静止开始运动(开始时刻,cd边与AB边重合),求:
(1)通过计算,在图2中画出线框从静止开始运动到cd边与CD边重合时(不考虑ab边离开斜面后线框的翻转),线框的速度-时间图象.
(2)线框abcd在整个运动过程中产生的焦耳热.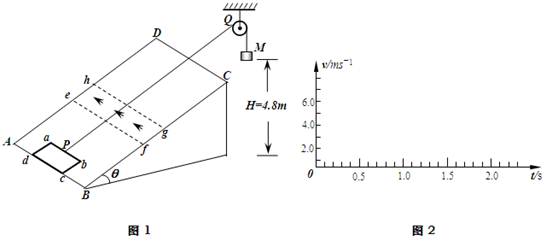
参考答案:(1)解法一:
如图所示,线框abcd由静止沿斜面向上运动,到ab与ef线重合过程中,线框受恒力作用,线框和重物以大小相等的加速度做匀加速运动,设为a1,则:
? 对M:Mg-T=Ma1
? 对m:T-mgsinθ=ma1
(或对系统直接列出:Mg-mgsinθ=(M+m)a1亦可)
联立得:①、②a1=Mg-mgsinθM+m=20-53=5m/s2?
设ab恰好要进入磁场时的速度为v0,则:v20=2a1s1
解得 v0=
本题解析:
本题难度:一般
5、计算题 如图所示,AB是两个同心圆,半径之比RA∶RB=2∶1,A、B是由相同材料,粗细一样的导体做成的,小圆B外无磁场,B内磁场的变化如图所示,求A、B中电流大小之比(不计两圆中电流形成磁场的相互作用).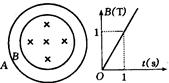
参考答案:1∶2
本题解析:在ε=ΔB/Δt·S中,S是磁场变化的面积.所以IA=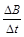 ·
·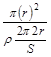 .IB=
.IB=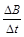 ·
·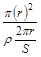 ,?所以IA∶IB=1∶2
,?所以IA∶IB=1∶2
本题难度:一般