时间:2017-08-07 16:26:09
1、简答题
(1)要使盒子在最高点时盒子与小球之间恰好无作用力，则该盒子做匀速圆周运动的周期为多少？
(2)若盒子以第（１）问中周期的
做匀速圆周运动，则当盒子运动到图示球心与O点位于同一水平面位置时，小球对盒子的哪些面有作用力，作用力为多大？
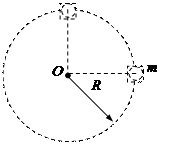
参考答案：
(1)
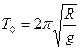?(2) 小球对盒子的右侧面和下侧面有作用力 4 mg和mg
本题解析：设此时盒子的运动周期为T0，因为在最高点时盒子与小球之间刚好无作用力，因此小球仅受重力作用．根据牛顿运动定律得：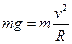
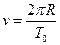? ?（１分）
?（１分）
解之得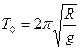：?（2分）
（2）设此时盒子的运动周期为T，则此时小球的向心加速度为：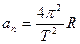
（1分）
由第一问知：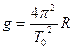
?且
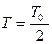?（1分）
由上述三式知：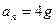
?（1分）
设小球受盒子右侧面的作用力为F，受上侧面的作用力为N，根据牛顿运动定律知：
在水平方向上：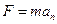
?（2分）
即：?
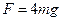?（1分）
在竖直方向上：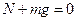
?（2分）
即：
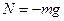?（1分）
因为F为正值、N为负值，所以小球对盒子的右侧面和下侧面有作用力，分别为:
4 mg和mg? （1分）
本题难度：一般
2、选择题 甲乙两小球质量相同，在光滑圆锥形漏斗的内壁做匀速圆周运动，如图所示，则有（ ）
A．ν甲＞ν乙
B．ω甲＞ω乙
C．a甲＞a乙
D．T甲＞T乙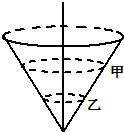
参考答案：为了分析计算的方便，我们把甲、乙两小球定义为A、B球．
对A、B两球进行受力分析，两球均只受重力和漏斗给的支持力FN．如图所示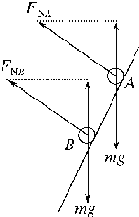
对A球由牛顿第二定律：
FNAsinα=mg----------------------①
FNAcosα=mvA2rA=mωA2rA-----------------------②
对B球由牛顿第二定律：
FNBsinα=mg----------------------③
FNBcosα=mvB2rB=mωB2rB-------------------------④
由两球质量相等可得FNA=FNB，所以C错误．
由②④可知，两球所受向心力相等．mvA2rA=mvB2rB，因为rA＞rB，所以vA＞vB，故A正确，B错误．
mωA2rA=mωB2rB，因为rA＞rB，所以ωA＜ωB，故又因为ω=2πT，所以TA＞TB，故D正确．
故选：AD．
本题解析：
本题难度：一般
3、简答题 质量为m的小球被系在轻绳一端，在竖直平面内作半径为R的圆周运动，运动过程中小球受到空气阻力的作用．设某一时刻小球通过轨道的最低点，此时绳子的张力为7mg，此后小球继续作圆周运动，经过半个圆周恰能通过最高点，则在此过程中小球克服空气阻力所做的功是多少？
参考答案：最低点?7mg-mg=mv12R
? v1=
本题解析：
本题难度：一般
4、选择题 如图所示，质量分别为m1、m2的小球A、B可以在光滑的水平杆上滑动，两球之间用一根水平细线相连，m1=2m2．当装置以角速度ω绕中心轴线匀速转动，达到稳定时，两球离轴的距离保持不变，则有（ ）
A．两球的向心力大小相等
B．r1=
| r2 2 |
参考答案：A、两小球所受的绳子的拉力提供向心力，所以向心力大小相等，角速度又相等，则有：
m1ω2r1=m2ω2r2
又m1=2m2．
解得：r1：r2=1：2，故AB正确，
C、根据向心力的表达式，Fn=man；由于向心力大小相等，则向心加速度与质量成反比，故C错误；
D、由A选项公式可知，向心力中均有角速度，因此可以相约去，则当ω增大时，仍处于原来状态，故D错误；
故选AB
本题解析：
本题难度：一般
5、选择题 一物体做匀加速直线运动，通过一段位移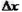
所用的时间为t1，紧接着通过下一段位移
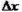所用时间为t2。则物体运动的加速度为
[? ]
A.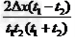 
?
B.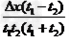
?
C.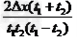
?
D.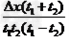
参考答案：A
本题解析：
本题难度：一般