时间:2017-08-05 17:58:00
1、选择题 如图所示,具有一定质量的小球A固定在轻杆一端,另一端挂在小车支架的O点。用手将小球拉至水平,此时小车静止于光滑水平面上,放手让小球摆下与B处固定的橡皮泥碰击后粘在一起,则在此过程中小车将? 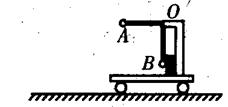
A.向右运动
B.向左运动
C.静止不动
D.小球下摆时,车向左运动后又静止
参考答案:D
本题解析:小球A和小车组成的系统在水平方向不受外力作用,动量守恒;系统初始总动量为零,在小球向下摆动过程中,小球A有向右运动的速度,故小车就会向左运动;当小球A和小车碰撞后合为一体,根据动量守恒,小车又会处于静止状态,D选项正确。
思路分析:小球A和小车组成的系统只在水平方向上动量守恒。
试题点评:本题考查某一方向上不受外力或合外力为零,动量守恒。
本题难度:简单
2、选择题 不定项选择
如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动。两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量均为6 kg·m/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4 kg·m/s,则( ? )

参考答案:B
本题解析:
本题难度:一般
3、简答题 如图12所示,水平平板小车质量为m=" 2kg," 其上左端放有一质量为M=6kg的铁块,铁块与平板车间的动摩擦因数μ=0.5,今二者以10m/s的速度向右运动,并与墙发生弹性碰撞,使小车以大小相同的速度反弹回,这样多次进行,求:
① 欲使M不从小车上落下,小车至少多长?
② 第一次反弹后到最终状态,小车运动的总路程.(小车与水平面的摩擦不计,g=10m/s2 )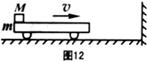
参考答案:(1)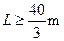 (2)
(2)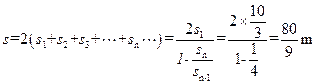
本题解析:① 取平板车与铁块为研究系统,由M>m,系统每次与墙碰后m反向时,M仍以原来速度向右运动,系统总动量向右,故会多次反复与墙碰撞,每次碰后M都要相对m向右运动,直到二者停在墙边,碰撞不损失机械能,系统的动能全在M相对m滑动时转化为内能。设M相对m滑动的距离为s,则: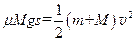 ?
?
解得: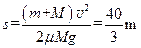 ?
?
欲便M不从小车上落下,则L≥s,故平长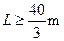 ?
?
② 小车第一次反弹向左以10m/s的速度做减速运动,直到速度为零,其加速度大小为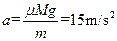 ? ( l 分)
? ( l 分)
故小车第一次向左的最大位移为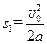 ,代入数据得
,代入数据得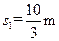 ?
?
设小车第n-1次碰前速度为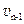 ,第n次碰前速度为
,第n次碰前速度为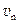 ,则第n-1次碰后到第n次碰前过程动量守恒,有:
,则第n-1次碰后到第n次碰前过程动量守恒,有: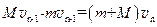 ,所以
,所以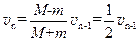 ?
?
第n-1次碰后小车反弹速度为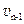 ,向左减速的最大位移为
,向左减速的最大位移为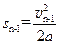 ?
?
随后向右加速距离为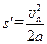 ,显然
,显然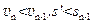 ,所以在碰前有相等速度
,所以在碰前有相等速度
第n次碰后向左运动的最大位移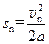 (1分),所以
(1分),所以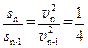 ,即成等比数列。小车运动的总路程为:
,即成等比数列。小车运动的总路程为: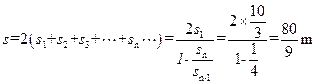
本题难度:一般
4、选择题 有一种硬气功表演,表演者平卧在地面,将一大石板置于他的身体上,另一个人将重锤举到高出并砸向石板,石板被砸碎,而表演者却安然无恙。假设重锤与石板撞击后二者具有相同的速度。表演者在表演时尽量挑选质量较大的石板。对这一现象,下面的说法正确的是
A.重锤在与石板撞击的过程中,重锤与石板的总机械能守恒
B.石板的质量越大,石板获得动量就越小
C.石板的质量越大,石板所受到的打击力就越小
D.石板的质量越大,石板获得的速度就越小
参考答案:D
本题解析:抽象为碰撞模型,碰撞中满足动量守恒定律、重锤的动能大于碰后重锤和石板的总动能,碰撞后两者速度相同属于能量损失最大的一类碰撞,A错误;石板质量越大,共同速度越小,重锤的动量损失越多,则石板获得的动量就越大,B错误、D正确;表演者挑选质量较大的石板,在打击时产生更大的打击力,石板就越容易砸碎,C错误。
本题难度:简单
5、计算题 光滑水平面上,用弹簧相连接的质量均为2 kg的A、B两物体都以v0=6 m/s速度向右运动,弹簧处于原长。质量为4 kg的物体C静止在前方,如图所示,B与C发生碰撞后粘合在一起运动,在以后的运动中,求:
(1)弹性势能最大值为多少?
(2)当A的速度为零时,弹簧的弹性势能为多少? 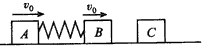
参考答案:解:(1)B、C碰撞瞬间,B、C的总动量守恒,由动量守恒定律得:
mBv0=(mB+mC)v
v=2 m/s
三个物体速度相同时弹性势能最大,由动量守恒定律得:
mAv0+mBv0= (mA+mB+mC)v共
v共=3m/s
设最大弹性势能为Ep,由能量守恒得: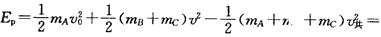 12 J
12 J
(2)当A的速度为零时,由动量定恒定律得:
mAv0+mBv0=(mB+mC)vBC
vBC=4 m/s
则此时的弹性势能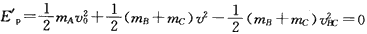
本题解析:
本题难度:困难