时间:2017-08-05 16:57:04
1、简答题 如图所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L.M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于匀强磁场中,磁场方向垂直于斜面向上.导轨和金属杆的电阻可忽路.让金属杆ab沿导轨由静止开始下滑,经过足够长的时间后,金属杆达到最大速度vm,在这个过程中,电阻R上产生的热量为Q.导轨和金属杆接触良好,它们之间的动摩擦因数为μ且μ<tanθ.已知重力加速度为g.
(1)求磁感应强度的大小;
(2)金属杆在加速下滑过程中,当速度达到v1(v1<vm)时,求此时杆的加速度大小;
(3)求金属杆从静止开始至达到最大速度的过程中下降的高度.
参考答案:
(1)当ab匀速运动时,金属杆的受力图如图所示(从前向后看的视图):图中Ff为滑动摩擦力,FN为斜面支持力,F安为感应电流的安培力,mg为导体棒的重力.这时导体棒匀速直线运动,其所受的合力为零,则有:
? mgsinθ=Ff+F安
? FN=mgcosθ,
由滑动摩擦力公式:Ff=μFN,
由安培力公式F安=BIL,由欧姆定律I=ER,由法拉第电磁感应定律得E=BLvm,得F安=B2L2vmR
解得:B=
本题解析:
本题难度:一般
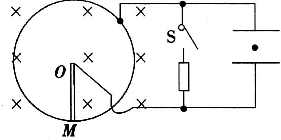
2、简答题 半径为a的圆环电阻不计,放置在垂直于纸面向里,磁感应强度为B的匀强磁场中,环内有一导体棒电阻为r,可以绕环匀速转动,将电阻R、开关S连接在环和棒的O端,将电容器极板水平放置,并联在R和开关S两端,如图所示.
(1)开关S断开,极板间有一电荷量为q、质量为m的带正电粒子恰好静止,试判断OM的转动方向和角速度的大小.
(2)当S闭合时,该带电粒子以
| 1 4 |
参考答案:(1)由于粒子带正电,恰好静止在电容器中,则电容器上极板带负电,由右手定则判断可知,OM应绕O沿逆时针方向转动.
粒子受力平衡,有mg=qUd
当S断开时,U=E
又OM产生的感应电动势为 E=12Ba2ω
解得ω=2mgdqBa2
(2)当S闭合时,根据牛顿第二定律得:mg-qU′d=m?g4
又U′=ER+rR
解得Rr=3
答:
(1)开关S断开,极板间有一电荷量为q、质量为m的带正电粒子恰好静止,OM的转动方向为逆时针,角速度的大小为2mgdqBa2.
(2)当S闭合时,该带电粒子以14g的加速度向下运动,则R是r的3倍.
本题解析:
本题难度:一般
3、计算题 一电阻为R的金属圆环,放在匀强磁场中,磁场与圆环所在平面垂直,如图(a)所示。已知通过圆环的磁通量随时间t的变化关系如图(b)所示,图中的最大磁通量φ0和变化周期T都是已知量,求:在t=0到t=2T的时间内,金属圆环所产生的电热Q。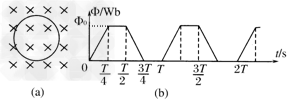
参考答案:解:在t=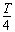 到t=
到t=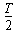 和在t=
和在t=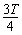 到t=T时间内,环中的感应电动势E2=0
到t=T时间内,环中的感应电动势E2=0
在t=0到t=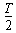 时间内,环中的感应电动势E=
时间内,环中的感应电动势E=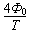
由欧姆定律可知在以上时段内,环中的电流为I3=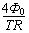
在t=0到t=2T时间内金属环所产生的电热Q=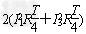
联立求解得Q=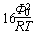
本题解析:
本题难度:一般
4、选择题 竖直放置的平行金属导轨AB、CD上端接有电阻R,置于磁感应强度为B的匀强磁场中,磁场方向与导轨平面垂直,如图所示.一质量为m的金属杆ab横跨在平行导轨上,且ab与导轨接触良好。若ab杆在竖直向上的外力F作用下匀速上升,在不计金属杆ab与导轨电阻,不计摩擦的情况下,则( )
A.拉力F所做的功等于电阻R上产生的热
B.拉力F与重力做功的代数和等于电阻R上产生的热
C.拉力F与重力做功的代数和等于电阻R上产生的热及杆ab重力势能增加量的和
D.拉力F所做的功等于电阻R上产生的热及杆ab重力势能增加量和安培力做功的和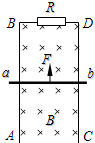
参考答案:B
本题解析:
本题难度:一般
5、选择题 如图所示,将一根绝缘硬金属导线弯曲成一个完整的正弦曲线形状,它通过两个小金属环a、b与长直金属杆导通,在外力F作用下,正弦形金属线可以在杆上无摩擦滑动.杆的电阻不计,导线电阻为R,ab间距离为2L,导线组成的正弦图形项部或底部到杆距离都是
| L 2 |
| B2L2v2 R |
| B2L3v 2R |
| B2L3v 4R |
| B2L2v2 4R |
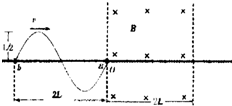
参考答案:金属导线产生的感应电动势瞬时值为e=Byv,y是有效切割长度.y=L2sinωt
得到 e=BLv2sinωt,ω=2πT=2π2Lv=πvL不变
则线圈中产生正弦式交变电流,其感应电动势的有效值为E=BLv2
本题解析:
本题难度:一般