时间:2017-08-05 16:48:11
1、计算题 如图所示，是一摩托车特技表演的轨道示意图。AB是距地面高为H的平台上的水平加速轨道，其长度为L，CD是半径为R的
竖直光滑圆弧轨道，CD轨道在最低点D与水平面相切，D点恰好又是紧接的竖直光滑圆形轨道的入口，该圆形轨道的出口与右侧水平减速轨道EF光滑相接。假设某总质量为m的摩托车（可视为质点）由A点从静止开始沿AB轨道做匀加速直线运动，到达B端时关闭发动机后水平飞出，刚好从C点沿切线方向进入圆弧轨道，运动过程中恰能通过圆形轨道的最高点P，最后从E点进入减速轨道直到停止。已知重力加速度为g，不计空气阻力。试求：
（1）摩托车在AB轨道上的加速度a；
（2）竖直圆形轨道的半径；
参考答案：（1）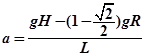
（2）
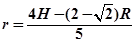
本题解析：摩托车运动分为三个阶段处理：AB段加速，BC段平抛、CDP段光滑曲线运动。设摩托车在AB轨道上的加速度为a，从B处飞出的速度为υ0，BC段平抛的竖直位移为h，到达C点的竖直分速度为υCy，水平分速度为υCx，竖直圆形轨道的半径为r，经过最高点P的速度为υ。
（1）对AB轨道上的加速过程有：2aL =υ02 ①1分
对BC段的平抛运动过程有：υcy2=2gh ②1分 υcx=υ0 ③1分
由几何关系可知，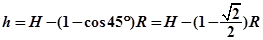
④1分
到达C点时的速度偏向角为45º，所以两分速度大小相等：υCx=υCy ⑤1分
联立①②③④⑤解得：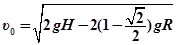
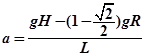⑥1分 ⑦2分
（2）以水平地面为参考平面，摩托车从B到P的过程机械能守恒，所以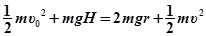
⑧2分
在P点由动力学原理得：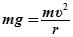 
⑨2分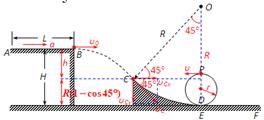
联立⑥⑧⑩解得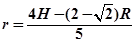： ⑩1分
考点：考查了圆周运动，平抛运动，机械能守恒
本题难度：一般
2、计算题 如图所示，在光滑水平面上，木块A的质量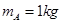
，木块B的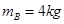质量
，质量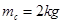
的木块C置于足够长的木块B上，B、C之间用一轻弹簧相拴接并且接触面光滑。开始时B、C静止，A以
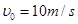的初速度向右运动，与B碰撞后B的速度为3.5 m／s，碰撞时间极短。求：
①A、B碰撞后A的速度。
②弹簧第一次恢复原长时C的速度。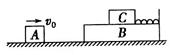
参考答案：①-4m/s ②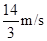
本题解析：①因碰撞时间极短，A、B碰撞时，C的速度为零，由动量守恒定律得
mAv0＝mAvA＋mBvB
解得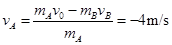
，方向与A的初速度方向相反
②第一次恢复原长，弹簧的弹性势能为零，设此时B的速度为vB′，C的速度为vC
由动量守恒定律得mBvB＝mBvB′＋mCvC
由机械能守恒定律得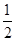
mBvB2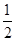＝mBvB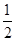′2＋mCvC2
得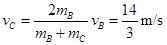
考点：动量守恒定律；机械能守恒定律
本题难度：一般
3、计算题 如图所示，质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂，摆长相同，均为l。现将绝缘球拉至与竖直方向成θ=60°的位置自由释放，摆至最低点与金属球发生弹性碰撞。在平衡位置附近存在垂直于纸面的磁场，已知由于磁场的阻尼作用，金属球总能在下一次碰撞前停在最低点处，重力加速度为g。求：
（1）第一次碰撞前绝缘球的速度v0；
（2）第一次碰撞后绝缘球的速度v1；
（3）经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于37°
（你可能用到的数学知识：sin37°=0.6，cos37°=0.8，0.812=0.656，0.813=0.531，0.814=0.430，0.815=0.349，0.816=0.282）
参考答案：（1）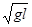
（2）
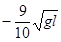（3）5
本题解析：（1）由机械能守恒定律得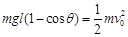 
①
解得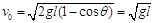 
（2）两球碰撞过程中动量守恒和机械能守恒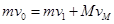
② 
③
联立②③解得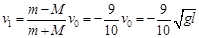
（3）设在第n次碰撞前绝缘球的速度为vn－1，碰撞后绝缘球、金属球的速度分别为vn和Vn。由于碰撞过程中动量守恒和机械能守恒，则
mvn－1=MVn+mvn ④
⑤
由④、⑤两式及M=19m解得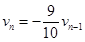
第n次碰撞后绝缘球的动能为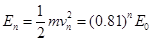
⑥
E0为第1次碰撞前绝缘球的动能，即初始能量。
得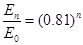
⑦
而绝缘球在θ=60°与θ=37°处的势能之比为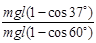
=0.4 ⑧
根据上面数学知识，0.814=0.430，0.815=0.349，因此，经过5次碰撞后θ将小于37°。
考点：机械能守恒定律；动量守恒定律.
本题难度：困难
4、计算题 如图所示，皮带在轮O1O2带动下以速度v匀速转动，皮带与轮之间不打滑。皮带AB段长为L，皮带轮左端B处有一光滑小圆弧与一光滑斜面相连接。物体无初速放上皮带右端后，能在皮带带动下向左运动，并滑上斜面。己知物体与皮带间的动摩擦因数为μ，且
参考答案：
本题解析：
本题难度：一般
5、选择题 从同一高度以相同的速率抛出质量相等的三个小球，分别做竖直上抛运动，竖直下抛运动，平抛运动，则它们从抛出到落地的过程，不计空气阻力，以下说法正确的是（ ）
A．运动的时间相等
B．加速度相同
C．落地时的速度相同
D．落地时的动能不相等
参考答案：B
本题解析：平抛运动在竖直方向上做自由落体运动，在同一高度自由落体运动的时间小于竖直上抛运动的时间，大于竖直下抛运动的时间，故A错误；竖直上抛运动、竖直下抛运动、平抛运动仅受重力，加速度都为g，故B正确；根据动能定理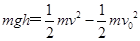
，知初动能相等，高度相同，则末动能相等．末速度的大小相等，但方向不同，所以落地速度不同，故CD错误。
考点：考查了抛体运动规律的应用
本题难度：一般