时间:2017-07-27 11:46:26
1、选择题 如图所示，用细线吊着一个质量为m的小球，使小球在水平面内做匀速圆周运动，关于小球运动的加速度，下列说法正确的是（ ）
A．加速度保持恒定不变
B．加速度的方向沿细线方向
C．加速度的方向沿圆周的半径指向圆心
D．因小球做的是匀速运动，所以没有加速度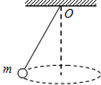
参考答案：小球受重力和绳子的拉力，两个力的合力提供圆周运动的向心力，加速度的方向始终指向圆心．故C正确，A、B、D错误．
故选C．
本题解析：
本题难度：一般
2、选择题 用一根细绳，一端系住一个质量为m的小球，另一端悬在光滑水平桌面上方h处，绳长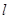
大于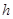
，使小球在桌面上做如图所示的匀速圆周运动．若使小球不离开桌面，其圆周运动的转速最大值是 (? )
A．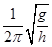
B．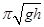
C．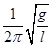
D．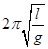
参考答案：A
本题解析：转速最大时，小球对桌面刚好无压力，则
即
?，其中
，所以
，故选A
点评：本题考查了结合实例的向心力的受力分析并建立等式求解的过程。在这类问题中最重要的是找到向心力的来源。
本题难度：简单
3、简答题 如图所示，AB为水平轨道，A、B间距离s=1.25m，BCD是半径为R=0.40m的竖直半圆形轨道，B为两轨道的连接点，D为轨道的最高点．有一小物块质量为m=1.0kg，小物块在F=10N的水平力作用下从A点由静止开始运动，到达B点时撤去力F，它与水平轨道和半圆形轨道间的摩擦均不计．g取10m/s2，求：
（1）撤去力F时小物块的速度大小；
（2）小物块通过D点瞬间对轨道的压力大小；
（3）小物块通过D点后，再一次落回到水平轨道AB上，落点和B点之间的距离大小．
参考答案：（1）当物块从A滑向B时，设在B点撤去F时速度大小为vB．
根据动能定理得：Fs=12mv2B
得 vB=5m/s
（2）小物块从B到D点瞬间，由动能定理得：
-mg?2R=12mv2D-12mv2B
解得：vD=3m/s
根据牛顿第二定律得：
? FD+mg=mv2DR
解得：FD=12.5N?
由牛顿第三定律知压力大小为FD′=FD=12.5N
（3）物块通过D点后做平抛运动，有：
?2R=12gt2
?x=vDt
解得：x=1.2m
答：（1）撤去力F时小物块的速度大小是5m/s；
（2）小物块通过D点瞬间对轨道的压力大小是12.5N；
（3）小物块通过D点后，再一次落回到水平轨道AB上，落点和B点之间的距离大小是1.2m．
本题解析：
本题难度：一般
4、填空题 半径为R的半球形碗内表面光滑，一质量为m的小球以角速度ω在碗内一水平面做匀速圆周运动，则该平面离碗底的距离h=______________。
参考答案：
本题解析：
本题难度：一般
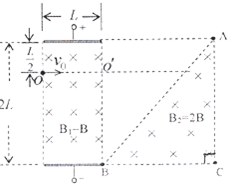
5、简答题 如图所示，平行板电容器板长为L，极板间距为2L，上板带正电，忽略极板外的电场．?O、O′是电容器的左右两侧边界上的点，两点连线平行于极板，且到上极板的距离为L/2．?在电容器右侧存在一个等腰直角三角形区域ABC，∠C=90°，底边BC与电容器的下极板共线，B点与下极板右边缘重合，顶点A与上极板等高．?在电容器和三角形区域内宥垂直纸面向里的匀强磁场，磁感应强度大小分别为B1=B、B2=2B．一带正电的粒子以初速度v0从O点沿着00′方向射入电容器，粒子的重力和空气阻力均不计．
（1）若粒子沿?00′做直线运动，进人三角形区域后，恰从顶点?A飞出，求两极板间的电压U和带电粒子的比荷
| q m |
参考答案：（1）粒子在电容器中受力平衡，故：
U2Lq=Bqv0①
由于三角形区域ABC为等腰直角三角形，故粒子进入磁场B2到从A射出的轨迹为14圆周，故半径：
R1=L2②
洛伦兹力提供向心力，由牛顿第二定律得：
2Bqv0=mv20R1③
由以上得，qm=v0BL④
（2）粒子在电容器中做类平抛运动，设飞出电场时侧向位移为y，速度方向偏转角为θ，则有：
y=12×Uq2Lm×(Lv0)2⑤
tanθ=yL2=2yL⑥
解①④⑤⑥得：y=L2，θ=45°⑦
速度大小为：v=
本题解析：
本题难度：一般