时间:2017-07-10 22:17:48
1、计算题 (18分)图所示为回旋加速器的示意图。它由两个铝制D型金属扁盒组成,两个D形盒正中间开有一条狭缝,两个D型盒处在匀强磁场中并接在高频交变电源上。在D1盒中心A处有离子源,它产生并发出的a粒子,经狭缝电压加速后,进入D2盒中。在磁场力的作用下运动半个圆周后,再次经狭缝电压加速。为保证粒子每次经过狭缝都被加速,设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致。如此周而复始,速度越来越 大,运动半径也越来越大,最后到达D型盒的边缘,以最大速度被导出。已知a粒子电荷量为q,质量为m,加速时电极间电压大小恒为U,磁场的磁感应强度为B,D型盒的半径为R,设 狭 缝 很 窄,粒子通过狭缝的时间可以忽略不计,设α粒子从离子源发出时的初速度为零。(不计α粒子重力)求: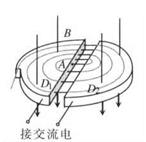
(1) α粒子第一次被加速后进入D2盒中时的速度大小;
(2) α粒子被加速后获得的最大动能Ek和交变电压的频率f;
(3)α粒子在第n次由D1盒进入D2盒与紧接着第n+1次由D1盒进入D2盒位置之间的距离Δx。
2、计算题 如图所示,质量为m,带电量为q(q>0)的粒子(重力不计),从离坐标原点为1.5a的 y轴上的P点,以速度大小为v0,方向与y轴正方向成θ=30°射入xoy坐标的第一象限,经过一个在第一象限内,边界形状为等腰梯形方向与xoy坐标面垂直匀强磁场区域,然后沿-x方向经过坐标原点0,进入相互垂直的匀强电场和匀强磁场中,其运动轨迹为虚线所示,该电场强度为E,方向沿-y轴方向,磁感应强度为B,方向垂直坐标面向外。
(1)画出最小的等腰梯形所处的位置和粒子运动轨迹,并求出此时的磁感应强度;
(2)粒子过坐标原点0后的运动可分解为x方向和y方向两分运动组成,已知y方向分运动为简谐运动;求粒子离x轴最远距离。
3、选择题 如图所示,质量为m,带电量为q的负粒子(重力不计)经历电压为U1加速电场加速度后,从平行板中心轴线进入后沿直线以速度v0飞出复合场,已知复合场区域的磁感应强度为B,电压为U2,极板距离为d。现欲使粒子以3v0的速度沿直线飞出,在保证粒子的比荷不变的情况下,下列方法可行的是: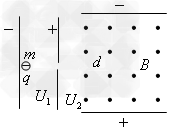
[? ]
A、保持其它参量不变,使U1变为原来的9倍
B、保持B、d不变,使使U1变为原来的9倍,U2变为原来的3倍
C、保持其它参量不变,使U2变为原来的3倍
D、保持B、U1、U2不变,使d变为原来的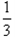 倍
倍
4、计算题 (12分)在足够大的绝缘光滑水平面上有一质量m=1.0×10-3kg、带电量q=1.0×10-10C的带正电的小球,静止在O点。以O点为原点,在该水平面内建立直角坐标系Oxy。在t0=0时突然加一沿x轴正方向、大小E1=2.0×106V/m的匀强电场,使小球开始运动。在t1=1.0s时,所加的电场突然变为沿y轴正方向、大小E2=2.0×106V/m的匀强电场。在t2=2.0s时所加电场又突然变为另一个匀强电场E3,使小球在此电场作用下在t3=3.0s时速度变为零。求: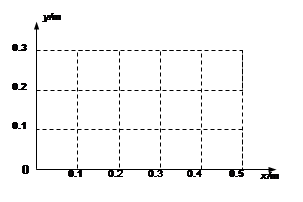
(1)在t1=1.0s时小球的速度v1的大小;
(2)在t2=2.0s时小球的位置坐标x2、y2;
(3)匀强电场E3的大小;
(4)请在图的坐标系中绘出该小球在这3s内的运动轨迹。
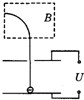
5、选择题 质量为m、电量为e的电子的初速为零,经电压为U的加速电场加速后进入磁感应强度为B的偏转磁场(磁场方向垂直纸面),其运动轨迹如图所示,则( )
A.加速电场的场强方向竖直向上
B.偏转磁场的磁场方向垂直纸面向里
C.能求出电子经加速电场加速后,开始进入磁场时的动能
D.能求出电子在磁场中所受的洛伦兹力的大小