时间:2017-07-10 22:17:48
1、计算题 如图（甲）所示，两光滑导轨都由水平、倾斜两部分圆滑对接而成，相互平行放置，两导轨相距L＝lm ，倾斜导轨与水平面成θ＝30°角，倾斜导轨的下面部分处在一垂直斜面的匀强磁场区I中，I区中磁场的磁感应强度B1随时间变化的规律如图（乙）所示，图中t1、t2未知。水平导轨足够长，其左端接有理想的灵敏电流计G和定值电阻R＝3Ω，水平导轨处在一竖直向上的匀强磁场区Ⅱ中，Ⅱ区中的磁场恒定不变，磁感应强度大小为B2＝1T ，在t＝0时刻，从斜轨上磁场I 区外某处垂直于导轨水平释放一金属棒ab，棒的质量m＝0.1kg，电阻r＝2Ω，棒下滑时与导轨保持良好接触，棒由斜轨滑向水平轨时无机械能损失，导轨的电阻不计。若棒在斜面上向下滑动的整个过程中，灵敏电流计G的示数大小保持不变，t2时刻进入水平轨道，立刻对棒施一平行于框架平面沿水平方向且与杆垂直的外力。（g取10m/s2）求：
（1）磁场区I在沿斜轨方向上的宽度d；
（2）棒从开始运动到刚好进入水平轨道这段时间内ab棒上产生的热量；
（3）若棒在t2时刻进入水平导轨后，电流计G的电流大小I随时间t变化的关系如图（丙）所示（I0未知），已知t2到t3的时间为0.5s，t3到t4的时间为1s，请在图（丁）中作出t2到t4时间内外力大小F随时间t变化的函数图像。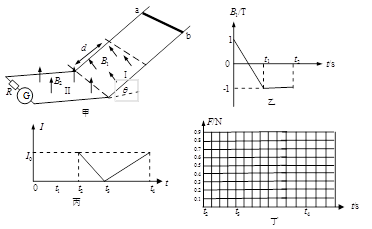
2、选择题 如图所示，正离子束以正对着荧光屏上的坐标原点O的水平速度v0先后通过沿竖直方向的匀强电场E和匀强磁场B，最后打在荧光屏的第Ⅲ象限中，则电场E和磁场B的方向是（ ）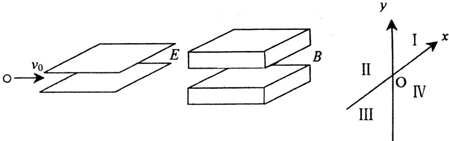
A．E竖直向上，B竖直向上
B．E竖直向下，B竖直向下
C．E竖直向上，B竖直向下
D．E竖直向下，B竖直向上
3、计算题 如图所示，虚线MO与水平线PQ相交于O，二者夹角θ=30°，在MO左侧存在电场强度为E、方向竖直向下的匀强电场，MO右侧某个区域存在磁感应强度为B、垂直纸面向里的匀强磁场，O点处在磁场的边界上，现有一群质量为m、电量为+q的带电粒子在纸面内以速度v（0≤v≤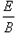
）垂直于MO从O点射入磁场，所有粒子通过直线MO时，速度方向均平行于PQ向左，不计粒子的重力和粒子间的相互作用力，求：?
（1）速度最大的粒子自O开始射入磁场至返回水平线POQ所用的时间．?
（2）磁场区域的最小面积．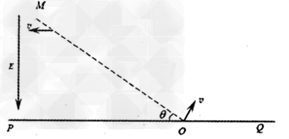
4、计算题 如图，半径为b、圆心为Q (b, 0) 点的圆形区域内有垂直纸面向里的匀强磁场，在第一象限内，虚线x=2b左侧与过圆形区域最高点P的切线y=b上方所围区域有竖直向下的匀强电场。其它的地方既无电场又无磁场。一带电粒子从原点O沿x轴正方向射入磁场，经磁场偏转后从P点离开磁场进入电场，经过一段时间后，最终打在放置于x=3b的光屏上。已知粒子质量为m、电荷量为q (q> 0), 磁感应强度大小为B, 电场强度大小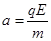
，粒子重力忽略不计。求：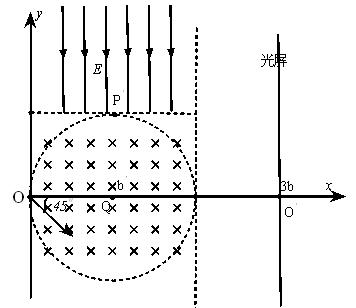
(1)粒子从原点O射入的速率v
(2)粒子从原点O射入至到达光屏所经历的时间t;
(3)若大量上述粒子以（1) 问中所求的速率，在xOy平 面内沿不同方向同时从原点O射入，射入方向分布 在图中45°范围内，不考虑粒子间的相互作用，求粒子先后到达光屏的最大时间差t0
(本题18分，第1小题3分，第2小题5分，第3小题10分)
5、选择题 下图为一“滤速器”装置的示意图a、b为水平放置的平行金属板，一束具有各种不同速率的电子沿水平方向经小孔O进入a、b两板之间为了选取具有某种特定速率的电子，可在a、b间加上电压，并沿垂直于纸面的方向加一匀强磁场，使所选电子仍能够沿水平直线OO"运动，由O"射出不计重力作用可能达到上述目的的办法是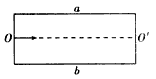 
[? ]
A.使a板电势高于b板，磁场方向垂直纸面向里
B.使a板电势低于b板，磁场方向垂直纸面向里
C.使a板电势高于b板，磁场方向垂直纸面向外
D.使a板电势低于b板，磁场方向垂直纸面向外