时间:2017-03-02 11:02:28
1、计算题 如图所示,质量为0.3kg的小车静止在足够长的光滑轨道上,小车下面挂一质量为0.1kg的小球B,在旁边有一支架被固定在轨道上,支架上O点悬挂一质量也为0.1kg的小球A。两球球心至悬挂点的距离L均为0.2m,当两球静止时刚好相切,两球球心位于同一水平线上,两悬线竖直并相互平行。将A球向左拉至悬线水平时由静止释放与B球相碰,碰撞过程中无机械能损失,两球相互交换了速度,取 。求:
。求: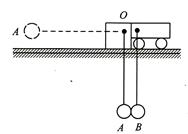
(1)碰撞后B球上升的最大高度。
(2)小车能获得的最大速度。
参考答案:(1)0.15m(2)1m/s
本题解析:本题考查连接体碰撞问题,在小球下落过程中机械能守恒,求出A到达最低点时速度再由动量守恒定律、机械能守恒定律求出上升的高度
(1)A球下落过程,由动能定理有
mAgl=mAv12/2? 2分
AB碰撞后瞬间,B的速度v2= v1
对B和车系统,在水平方向有mBv2=(M+mB)v? 2分
由机械能守恒定律有? mBv22/2="(" M+mB) v2/2+mBgh.? 2分
解得? h=0.15m? 1分
(2)? B回到最低点时,小车有最大速度vm,
对B和车系统,在水平方向有mBv2= mBv3+Mvm?2分
由机械能守恒定律有mBv22/2= mBv32/2+ Mvm2/2? 2分
所以? vm=1m/s?1分
本题难度:一般
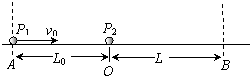
2、简答题 如图所示,在光滑绝缘水平面上,不带电的绝缘小球P2静止在O点.带正电的小球P1以速度v0从A点进入AB区域.随后与P2发生正碰后反弹,反弹速度为
| 2 3 |
| 4L0 3 |
| qE0 m1 |
| 4v02 3L0 |
参考答案:(1)碰撞后P1以速度v1=23v0向左做匀减速直线运动,设最大距离为s,由运动学公式有
v12=2as①
v1=at②
由牛顿第二定律有
qE0=m1a③
又qE0m1=4v023L0④
联立解得
s=16L0⑤
所需时间t=L02v0 ⑥
(2)设碰后P2速度为v2,以v0方向为正方向,由动量守恒:
m1v0=m1(-23v0)+m2v2⑦
设P1、P2碰撞后又经△t时间在OB区间内能再次发生碰撞,
P1位移为s1,P2位移为s2,由运动学公式,有
s1=-23v0△t+12a△t2⑧
s2=v2△t⑨
s1=s2⑩
联立解得
s2=L02<L=4L03两球能在OB区间内再次发生碰撞.
答:(1)碰撞后小球P1向左运动的最大距离为L06.所需时间为L02v0.
(2)两球能在OB区间内再次发生碰撞.
本题解析:
本题难度:一般
3、选择题 如图所示,光滑圆槽的质量为M,静止在光滑的水平面上,其内表面有一小球被细线吊着恰位于槽的边缘处,如果将线烧断,则小球滑到另一边的最高点时,圆槽的速度为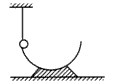
[? ]
A.0
B.向左
C.向右
D.无法确定
参考答案:A
本题解析:
本题难度:一般
4、填空题 光滑水平面上两小球a、b用不可伸长的松弛细绳相连。开始时a球静止,b球以一定速度运动直至绳被拉紧,然后两球一起运动,在此过程中两球的总动量 (填“守恒”或“不守恒”);机械能 (填“守恒”或“不守恒”)。
参考答案:守恒 不守恒
本题解析:将a b组成系统,对系统受力分析知合外力为零,故系统动量守恒;而在此过程拉力对b做负功,机械能不守恒。
本题难度:一般
5、选择题 两球A、B在光滑水平面上沿同一直线,同一方向运动,mA="1" kg,mB="2" kg,VA="6" m/s,VB="2" m/s。当A追上B并发生碰撞后,两球A、B速度的可能值是( )
A. VA′="5" m/s, VB′="2.5" m/s B. VA′="2" m/s, VB′="4" m/s
C. VA′=-4 m/s, VB′="7" m/s D. VA′="7" m/s, VB′="1.5" m/s
参考答案:B
本题解析:考虑实际情况,碰撞后A球速度不大于B球的速度,因而AD错误,BC满足;两球碰撞过程,系统不受外力,故碰撞过程系统总动量守恒,ABCD均满足;根据能量守恒定律,碰撞后的系统总动能应该小于或等于碰撞前的系统总动能,碰撞前总动能为22J,B选项碰撞后总动能为18J,C选项碰撞后总动能为57J,故ACD错误,B满足;
故选B.
考点:动量守恒定律;机械能守恒定律.
点评:本题碰撞过程中动量守恒,同时要遵循能量守恒定律,不忘联系实际情况,即后面的球不会比前面的球运动的快!
本题难度:一般