时间:2017-03-02 11:02:28
1、计算题 (9分)如图所示,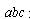 是光滑的轨道,其中
是光滑的轨道,其中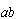 是水平的,
是水平的,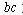 为与
为与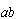 相切于竖直平面内的半圆,半径
相切于竖直平面内的半圆,半径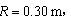 质量
质量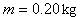 的小球
的小球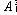 静止在轨道上,另一质量
静止在轨道上,另一质量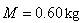 的小球
的小球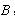 ,以初速度
,以初速度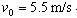 与小球
与小球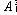 正碰。已知相碰后小球
正碰。已知相碰后小球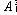 经过半圆的最高点
经过半圆的最高点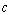 落到轨道上距
落到轨道上距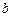 点
点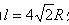 处,重力加速度
处,重力加速度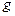 取10m/s2,
取10m/s2,
求:
(1)碰撞结束时,小球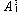 和
和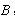 的速度大小;
的速度大小;
(2)试论证小球 是否能沿着半圆轨道到达
是否能沿着半圆轨道到达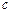 点。
点。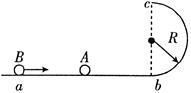
2、计算题 如图所示,小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离为h。物块B质量是小球的5倍,置于粗糙的水平面上且位于O点正下方,物块与水平面间的动摩擦因数为μ。现拉动小球使线水平伸直,小球由静止开始释放,运动到最低点时与物块发生正碰(碰撞时间极短),反弹后上升至最高点时到水平面的距离为 。小球与物块均视为质点,不计空气阻力,重力加速度为g,求碰后物块的速度。
。小球与物块均视为质点,不计空气阻力,重力加速度为g,求碰后物块的速度。
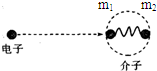
3、选择题 介子有两个夸克构成,而夸克之间的相互作用相当复杂.研究介子可通过用高能电子与之作非弹性碰撞来进行.由于碰撞过程难于分析,为掌握其主要内涵,人们发展了一种简化了的“分粒子”模型.其主要内容为:电子只和介子的某部分(比如其中一个夸克)作弹性碰撞.碰撞后的夸克再经过介子内的相互作用把能量和动量传给整个介子.
该物理现象可用下面的典型模型来描述如图所示:一个质量为M及动能为E的电子,与介子的一个质量为m1的夸克作弹性碰撞,介子里另一个夸克的质量为m2(m1≠m2),夸克间以一无质量的弹簧相连.碰撞前夸克处于静止状态,弹簧处于静止状态,弹簧处于自然长度L.所有运动都是一维的,忽略一切相对论效应.则碰撞后运动过程中夸克m2可能具有的动能为( )
A.Ek=
| Mm2 (M+m1)2(m1+m2)2 |
(M+m1)2(m1+m2)2 |
| 18Mm2 (M+m1)2(m1+m2)2 |
| 4Mm1 (M+m1)2 |
4、简答题 某同学用如图1所示装置,通过半径相同的A、B两球的碰撞来验证动量守恒定律.
(1)实验中必须要求的条件是______
A.斜槽轨道尽量光滑以减少误差
B.斜槽轨道末端的切线必须水平
C.入射球和被碰球的质量必须相等,且大小相同
D.入射球每次必须从轨道的同一位置由静止滚下
(2)在以下选项中,哪些是本次实验必须进行的测量?
A.水平槽上未放B球时,测量A球落点位置到O点的距离
B.A球与B球碰撞后,测量A球落点位置到O点的距离
C.测量A球或B球的直径
D.测量A球和B球的质量(或两球质量之比)
E.测量G点相对于水平槽面的高度
答:______(填选项号).
(3)某次实验中得出的落点情况如图2所示,假设碰撞过程中动量守恒,则入射小球质量m1和被碰小球质量m2之比为______.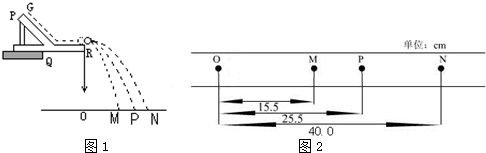
5、计算题 如图所示,光滑水平面上静止一质量为M=0.98kg的物块。紧挨平台右侧有传送带,与水平面成30°角,传送带底端A点和顶端B点相距L=3m。一颗质量为m=0.02kg的子弹,以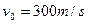 的水平向右的速度击中物块并陷在其中。物块滑过水平面并冲上传送带,物块通过A点前后速度大小不变。已知物块与传送带之间的动摩擦因数
的水平向右的速度击中物块并陷在其中。物块滑过水平面并冲上传送带,物块通过A点前后速度大小不变。已知物块与传送带之间的动摩擦因数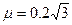 ,重力加速度g=10m/s2。
,重力加速度g=10m/s2。
(1)如果传送带静止不动,求物块在传送带上滑动的最远距离;
(2)如果传送带匀速运行,为使物块能滑到B端,求传送带运行的最小速度。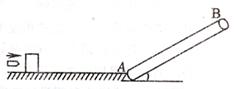
(3)若传送带以某一速度匀速运行时,物块恰能以最短时间从A端滑到B端,求此过程中传送带与物块间产生的热量。