时间:2017-03-02 10:41:12
1、计算题 在竖直平面内,以虚线为界分布着如图所示的匀强电场和匀强磁场,其中匀强电场方向向下,大小为E;匀强磁场垂直纸面向里,磁感应强度大小为B。虚线与水平线之间的夹角为θ=45°,一带电粒子以速度v0水平射入匀强磁场,已知带负电粒子电荷量为q,质量为m,(重力忽略不计,电场、磁场区域足够大)。
(1)求带电粒子第1次通过虚线时距O点的距离?
(2)求带电粒子第3次通过虚线时所经历的时间?
(3)求带电粒子第4次通过虚线时距O点的距离? 
参考答案:解:如图所示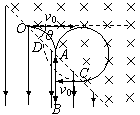 (1)
(1)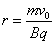
解得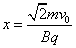
(2)在磁场中运动时间为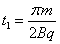
在电场中a=qE/m
运动时间为t2=2v0/a=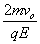
再一次在磁场中运动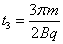
所以总时间t=
(3)再次进入电场中做类平抛运动
x2=v0t4
y=at42/2
x2=y
得x2=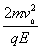
所以距离O点距离为Δx=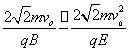
本题解析:
本题难度:困难
2、选择题 在如图所示的空间中,存在场强为E的匀强电场,同时存在沿x轴负方向,磁感应强度为B的匀强磁场。一质子(电荷量为e)在该空间恰沿y轴正方向以速度v匀速运动,据此可以判断出
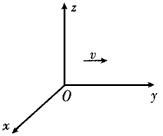
[? ]
参考答案:C
本题解析:
本题难度:一般
3、计算题 如题25图所示,在直角坐标xOy平面y轴左侧(含y轴)有一沿y轴负向的匀强电场,一质量为m,电量为q的带正电粒子从x轴上P处以速度v0沿x轴正向进入电场,从y轴上Q点离开电场时速度方向与y轴负向夹角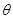 =30°,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小
=30°,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小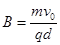 ,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求:
,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求: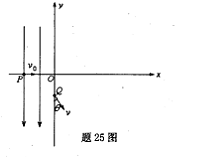
(1)电场强度大小E;
(2)如果有界匀强磁场区域为半圆形,求磁场区域的最小面积;
(3)粒子从P点运动到O点的总时间.
参考答案:(1)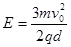 (2)
(2)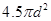 (3)
(3)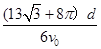
本题解析:首先根据平抛运动及动能定理求出电场强度;画出运动轨迹,求出半径,根据几何关系求出最小面积;分步求出各段的时间,最后求和得出总时间。
(1)设粒子从Q点离开电场时速度大小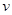
由粒子在匀强电场中做类平抛运动得: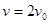 (1分)
(1分)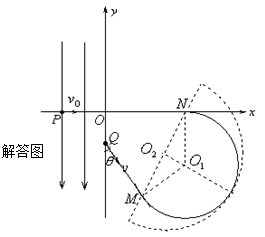
由动能定理得?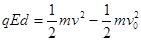 ?(2分)
?(2分)
解得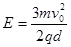 (1分)
(1分)
(2)设粒子从M点进入、N点离开半圆形匀强磁场区域
粒子在磁场中做匀速圆周运动半径为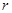 ,圆心为
,圆心为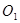 ,如解答图所示
,如解答图所示
由洛伦兹力提供向心力,得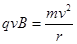 ?
?
解得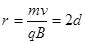 (2分)
(2分)
若半圆形磁场区域的面积最小,则半圆形磁场区域的圆心为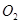
可得半径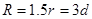 (2分)半圆形磁场区域的最小面积
(2分)半圆形磁场区域的最小面积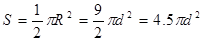 (2分)
(2分)
(3)设粒子在匀强电场中运动时间为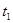
粒子从Q点离开电场时沿y轴负向速度大小为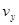 ?有
?有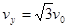
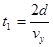 ?解得
?解得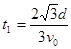 (2分)
(2分)
设粒子在磁场中做匀速圆周运动时间为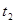 ?有
?有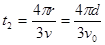 (2分)
(2分)
粒子在QM、NO间做匀速直线运动时间分别为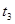 、
、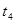
由几何关系可得QM距离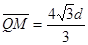 ?得
?得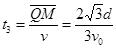 (2分)
(2分)
NO间距离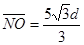 ?得
?得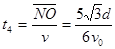 (2分)
(2分)
粒子从P点运动到O点的总时间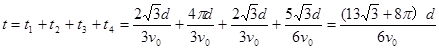 (1分)
(1分)
本题难度:一般
4、计算题 (10分)如图所示,一质量为m、电荷量为q的带负电的粒子,从A点射入宽度为d、磁感应强度为B的匀强磁场,MN、PQ为该磁场的边界线,磁场方向垂直于纸面向里,带电粒子射入时的初速度方向与下边界成θ=45°,且粒子恰好没有从MN边界射出,不计粒子所受重力,求该带电粒子初速度v0。
参考答案: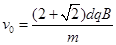 和
和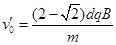
本题解析:由题意知,带电粒子恰好不能从MN边界射出时有两种可能的情况均满足题意。若带电粒子初速度向左上方和带电粒子初速度向右上方时粒子轨迹与磁场上边界相切,作出两种情况的粒子运动轨迹,如图所示。?①
设带电粒子初速度向右上方时轨迹半径为R1,则由牛顿第二定律和几何关系有: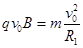 ?②
?②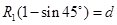 ?③
?③
联解②③得: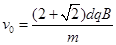 ?④
?④
设粒子初速度向左上方时轨迹半径为R2,则由牛顿第二定律和几何关系有: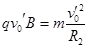 ?⑤
?⑤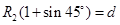 ?⑥
?⑥
联解⑤⑥得: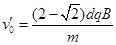 ?⑦
?⑦
评分参考意见:本题共10分,其中①②⑤式2分,③④⑥⑦式各1分;若有其他合理解法且答案正确,可同样给分。
本题难度:一般
5、计算题 如图所示,与水平面成37°的倾斜轨道AC,其延长线在D点与半圆轨道DF相切,全部轨道为绝缘材料制成且位于竖直面内,整个空间存在水平向左的匀强电场,MN的右侧存在垂直于纸面向里的匀强磁场(C点在MN边界上)。一质量为0.4 kg的带电小球沿轨道AC下滑,至C点时速度为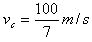 ,接着沿直线CD运动到D处进入半圆轨道,进入时无动能损失,且恰好能通过F点,在F点速度vF=4 m/s,(不计空气阻力,g=10 m/s2,cos37°=0.8)求:
,接着沿直线CD运动到D处进入半圆轨道,进入时无动能损失,且恰好能通过F点,在F点速度vF=4 m/s,(不计空气阻力,g=10 m/s2,cos37°=0.8)求:
(1)小球带何种电荷?
(2)小球在半圆轨道部分克服摩擦力所做的功。
(3)小球从F点飞出时磁场同时消失,小球离开F点后的运动轨迹与直线AC(或延长线)的交点为G(G点未标出),求G点到D点的距离。 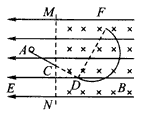
参考答案:解:(1)正电荷
(2)依题意可知小球在CD间做匀速直线运动
在D点速度为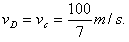
在CD段受重力、电场力、洛伦兹力,且合力为0,设重力与电场力的合力为F,F=qvCB
又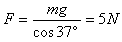
解得: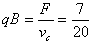
在F点处由牛顿第二定律可得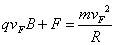
把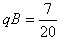 代入得,R=1 m
代入得,R=1 m
小球在DF段克服摩擦力做功W,由动能定律可得: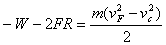
W=27.6 J
(3)小球离开F点后做类平抛运动,其加速度为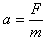
由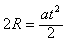 ,得
,得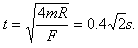
交点G与D点的距离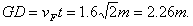
本题解析:
本题难度:困难