时间:2017-03-02 10:41:12
1、选择题 关于干簧管,下列说法正确的是( ? )
A.干簧管接入电路中相当于开关的作用
B.干簧管是根据热胀冷缩的原理制成的
C.干簧管接入电路中相当于电阻的作用
D.干簧管是作为电控元件以实现自动控制的
参考答案:AD
本题解析:由于干簧管是一种磁敏开关。它的两个触点由特殊材料制成,被封装在真空的玻璃管里。只要用磁铁接近它,干簧管两个节点就会吸合在一起,使电路导通。故干簧管在电路中相当于开关的作用,A正确;B、C均不对;D是正确的。
本题难度:简单
2、计算题 (18分)
如图甲,电阻不计的轨道MON与PRQ平行放置,ON及RQ与水平面的倾角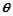 =53°,MO及PR部分的匀强磁场竖直向下,ON及RQ部分的磁场平行轨道向下,磁场的磁感应强度大小相同,两根相同的导体棒ab和cd分别放置在导轨上,与导轨垂直并始终接触良好。棒的质量m=1.0kg,R=1.0
=53°,MO及PR部分的匀强磁场竖直向下,ON及RQ部分的磁场平行轨道向下,磁场的磁感应强度大小相同,两根相同的导体棒ab和cd分别放置在导轨上,与导轨垂直并始终接触良好。棒的质量m=1.0kg,R=1.0 ,长度与导轨间距相同,L=1.0m,棒与导轨间动摩擦因数
,长度与导轨间距相同,L=1.0m,棒与导轨间动摩擦因数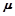 =0.5,现对ab棒施加一个方向向右,大力随乙图规律变化的力F的作用,同时由静止释放cd棒,则ab棒做初速度为零的匀加速直线运动,g取10m/s2,求
=0.5,现对ab棒施加一个方向向右,大力随乙图规律变化的力F的作用,同时由静止释放cd棒,则ab棒做初速度为零的匀加速直线运动,g取10m/s2,求
(1)ab棒的加速度大小;
(2)磁感应强度B的大小;
(3)若已知在前2s内外力做功W=30J,求这一过程中电路产生的焦耳热;
(4)求cd棒达到最大速度所需的时间.
参考答案:(1) 1m/s2(2) 2T(3) Q=18J(4)t=5s
本题解析:(1)对ab棒:f=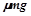 ? v=at
? v=at
F-BIL-f=ma
F=m(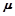 g+a)+
g+a)+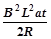 ?……………(1)
?……………(1)
a=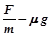 =1m/s2
=1m/s2
(2)当t=2s时,F=10N?由(1)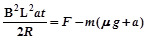
B=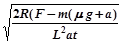 =2T
=2T
(3)0-2s过程中,对a、b棒,由动能定理
知:x=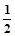 at2=2m? v=at=2m/s
at2=2m? v=at=2m/s
W-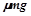 x-Q=
x-Q=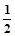 mv2
mv2
Q=18J
(4)当时间为t时,cd棒平衡,速度最大
N′=BIL+mgcos53°
f=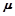 N′
N′
mgsin53°=f
mgsin53°=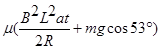
解得:t=5s
本题考查牛顿运动定律与电磁感应的结合,难度较大,导体棒在运动过程中受到重力、安培力和摩擦力,由牛顿第二定律列式求解,在2s时刻由牛顿第二定律求出安培力,根据导体棒做匀变速直线运动的规律可求出磁感强度,在第三问中有关能量变化,可利用动能定理求解
本题难度:一般
3、计算题 (21分)
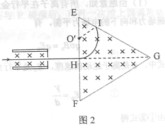
图中左边有一对平行金属板,两板相距为d,电压为V;两板之间有匀强磁场,磁感应强度大小为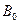 ,方向平行于板面并垂直于纸面朝里。图中右边有一边长为a的正三角形区域EFG(EF边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入金属板之间,沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域。不计重力。
,方向平行于板面并垂直于纸面朝里。图中右边有一边长为a的正三角形区域EFG(EF边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入金属板之间,沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域。不计重力。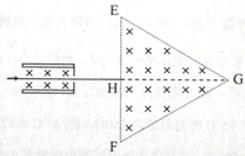
(1)已知这些离子中的离子甲到达磁场边界EG后,从边界EF穿出磁场,求离子甲的质量。
(2)已知这些离子中的离子乙从EG边上的I点(图中未画出)穿出磁场,且GI长为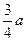 。求离子乙的质量。
。求离子乙的质量。
(3)若这些离子中的最轻离子的质量等于离子甲质量的一半,而离子乙的质量是最大的,问磁场边界上什么区域内可能有离子到达。
参考答案:
(1)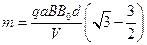 ?
?
(2)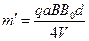 ?
?
(3)所以,磁场边界上可能有离子到达的区域是: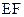 边上从
边上从 到
到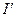 点。
点。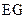 边上从
边上从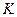 到
到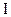 。
。
本题解析:(21分)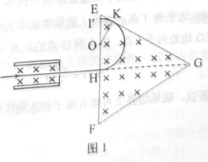
(1)由题意知,所有离子在平行金属板之间做匀速直线运动,它所受到的向上的磁场力和向下的电场力平衡,有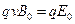 ?①?
?①?
式中,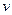 是离子运动的速度,
是离子运动的速度,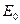 是平行金属板之间的匀强电场的强度,有
是平行金属板之间的匀强电场的强度,有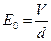 ?②?
?②?
由①②式得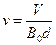 ?③?
?③?
在正三角形磁场区域,离子甲做匀速圆周运动。设离子甲质量为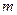 ,由洛仑兹力公式和牛顿第二定律有
,由洛仑兹力公式和牛顿第二定律有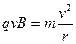 ?④
?④
式中,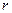 是离子甲做圆周运动的半径。离子甲在磁场中的运动轨迹为半圆,圆心为
是离子甲做圆周运动的半径。离子甲在磁场中的运动轨迹为半圆,圆心为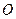 :这半圆刚好与
:这半圆刚好与 边相切于
边相切于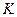 ,与
,与 边交于
边交于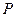 点。在
点。在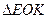 中,
中,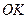 垂直于
垂直于 。由几何关系得
。由几何关系得
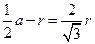 ?⑤
?⑤
由⑤式得
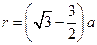 ?⑥
?⑥
联立③④⑥式得,离子甲的质量为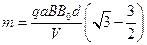 ?⑦?
?⑦?
(2)同理,由洛仑兹力公式和牛顿第二定律有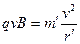 ?⑧
?⑧
式中,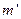 和
和 分别为离子乙的质量和做圆周运动的轨道半径。离子乙运动的圆周的圆心
分别为离子乙的质量和做圆周运动的轨道半径。离子乙运动的圆周的圆心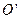 必在
必在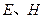 两点之间,又几何关系有
两点之间,又几何关系有 ?⑨
?⑨
由⑨式得
?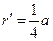 ?⑩
?⑩
联立③⑧⑩式得,离子乙的质量为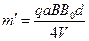 ?(11)
?(11)
(1)?对于最轻的离子,其质量为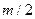 ,由④式知,它在磁场中做半径为
,由④式知,它在磁场中做半径为 的匀速圆周运动。因而与
的匀速圆周运动。因而与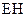 的交点为
的交点为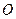 ,有
,有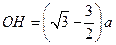 ?(12)
?(12)
(2)当这些离子中的离子质量逐渐增大到m时,离子到达磁场边界上的点的位置从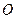 点沿
点沿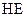 边变到
边变到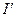 点;当离子质量继续增大时,离子到达磁场边界上的点的位置从
点;当离子质量继续增大时,离子到达磁场边界上的点的位置从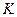 点沿
点沿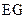 边趋向于
边趋向于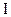 点。
点。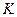 点到
点到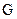 点的距离为
点的距离为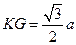 ?(13)
?(13)
(3)所以,磁场边界上可能有离子到达的区域是: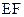 边上从
边上从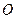 到
到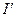 点。
点。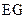 边上从
边上从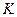 到
到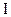 。
。
本题难度:一般
4、计算题 如图所示,第II象限中存在竖直向下的匀强电场,在x轴的下方L处存在一个处置纸面向外的单边界匀强磁场。今有一个电量为+q、质量为m的粒子(不计重力)从A点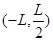 处以速度V0水平射入电场,恰好从坐标原点O处飞出,运动一段时间之后进入匀强磁场,并在磁场中经过P点(
处以速度V0水平射入电场,恰好从坐标原点O处飞出,运动一段时间之后进入匀强磁场,并在磁场中经过P点(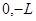 )。求:
)。求:
(1)平行板间的电场强度的大小;
(2)匀强磁场的磁感应强度的大小;
(3)粒子从A点运动到P点的时间。
参考答案:(1) 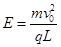 ,(2)
,(2) 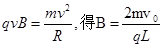 ,(3)
,(3) 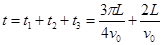
本题解析:(1)电场中,类平抛。
水平: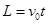 ?
?
竖直: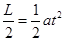 ?
?
且: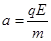 ?
?
联立得: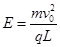 (1分)
(1分)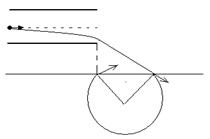
(2)飞出电场瞬间竖直速度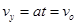 ?
?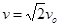 ?
?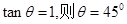 (2分)
(2分)
粒子进入以450进入磁场,轨迹如图示。
由几何关系可得: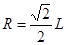 (2分)
(2分)
因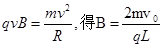 (2分)
(2分)
(3)由(1)可知电场中运动时间: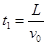 ?(不计分)
?(不计分)
出电场到磁场匀速直线运动用时: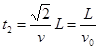 (2分)
(2分)
磁场中用时: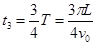 (2分)
(2分)
总用时: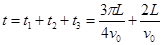 (2分)
(2分)
本题难度:一般
5、计算题 (18分)如图所示,x轴上方有一匀强磁场,磁感应强度为B,磁场方向垂直于纸面向里。X轴下方有一匀强电场,电场强度为E、方向与y轴的夹角θ=45°且斜向上方。现有一质量为m电量为q的正离子,以速度v0由y轴上的A点沿y轴正方向射入磁场,该离子在磁场中运动一段时间后从x轴上的C点(图中未画出)进入电场区域,离子经C点时的速度方向与电场方向相反。 不计离子的重力,设磁场区域和电场区域足够大, 求: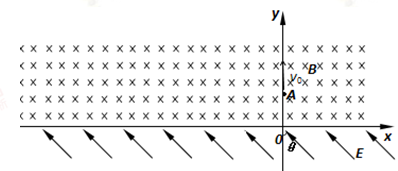
(1)C点的坐标;
(2)离子从A点出发到第三次穿越x轴时的运动时间;
(3)回答:离子从第三次过x轴到第四次过x轴的过程在做什么运动。并大致画出离子前四次穿越x轴在磁场和电场区域中的运动轨迹。
参考答案:(1)C点坐标为(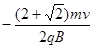 ,0)。(2)
,0)。(2)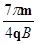 +
+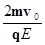 ;(3)类平抛运动,轨迹如下图:
;(3)类平抛运动,轨迹如下图: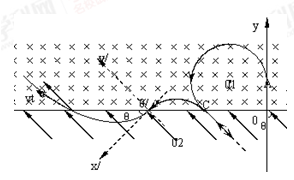
本题解析:(1)磁场中带电粒子在洛仑兹力作用下做圆周运动,故有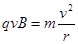 ①
①
由几何知识知,xC= (r+rcos450)=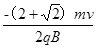 ③
③
故,C点坐标为(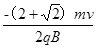 ,0) ③
,0) ③
(2)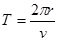 =
=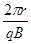 ④
④
设粒子从A到C的时间为t1,设粒子从A到C的时间为t1,由题意知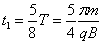 ⑤
⑤
设粒子从进入电场到返回C的时间为t2,其在电场中做匀变速运动,由牛顿第二定律和运动学知识,有 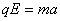 ⑥
⑥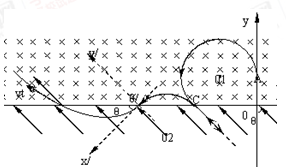
及 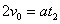 ⑦
⑦
联立⑥⑦解得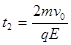 ⑧
⑧
设粒子再次进入磁场后在磁场中运动的时间为t3,由题意知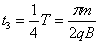 ⑨
⑨
故而,设粒子从A点到第三次穿越x轴的时间为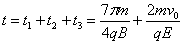
考点:带电粒子在电场中的运动(类平抛运动)、带电粒子在匀强磁场中的运动
本题难度:困难