时间:2017-03-02 10:41:12
1、计算题 竖直放置的两块足够长的平行金属板间有匀强电场。其电场强度为E,在该匀强电场中,用轻质绝缘丝线悬挂质量为m的带电小球,丝线跟竖直方向成θ角时小球恰好平衡,此时小球离右板距离为b,如图所示,问:
(1)小球所带电荷的电性如何?电荷量多少?
(2)若剪断丝线,小球碰到金属板需多长时间?
参考答案:(1)小球所带电荷为正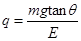 ?
?
(2)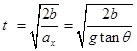
本题解析:(1)小球所带电荷为正?(2分)
小球受到水平向右的电场力、竖直向下的重力和丝线拉力三力平衡: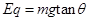 ?
?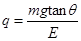 ?(4分)
?(4分)
(2)小球在水平方向做初速度为零的匀加速直线运动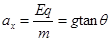 ?
?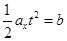 ?
?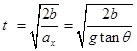 ?(4分)
?(4分)
点评:本题难度较小,粒子能够做直线运动的条件是合外力的方向与速度方向在同一条直线上
本题难度:一般
2、计算题 单位时间内流过管道横截面的液体体积叫做液体的体积流量(以下简称流量)。有一种利用电磁原理测量非磁性导电液体(如自来水、啤酒等)流量的装置,称为电磁流量计,它主要由将流量转换为电压信号的传感器和显示仪表两部分组成。
传感器的结构如图所示,圆筒形测量管内壁绝缘,其上装有一对电极a和c,a、c间的距离等于测量管内径D,测量管的轴线与a、c的连线方向以及通电线圈产生的磁场方向三者相互垂直,当导电液体流过测量管时,在电极a、c间出现感应电动势E,并通过与电极连接的仪表显示出液体的流量Q。设磁场均匀恒定,磁感应强度为B。 
(1)已知D=0.40 m,B=2.5×10-3 T,Q=0.12 m3/s,设液体在测量管内各处流速相同,试求E的大小(π取3.0);
(2)一新建供水站安装了电磁流量计,在向外供水时流量本应显示为正值,但实际显示却为负值。经检查,原因是误将测量管接反了,即液体由测量管出水口流入,从入水口流出。因水已加压充满管道,不便再将测量管拆下重装,请你提出使显示仪表的流量指示变为正值的简便方法;
(3)显示仪表相当于传感器的负载电阻,其阻值记为R。a、c间导电液体的电阻r随液体电阻率的变化而变化,从而会影响显示仪表的示数。试以E、R、r为参量,给出电极a、c间输出电压U的表达式,并说明怎样可以降低液体电阻率变化对显示仪表示数的影响。
参考答案:解:(1)导电液体通过测量管时,相当于导线做切割磁感线的运动。在电极a、c间切割磁感线的液柱长度为D,设液体的流速为v,则产生的感应电动势为E=BDv ①
由流量的定义,有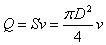 ?②
?②
①、②式联立解得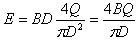
代入数据得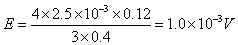
(2)能使仪表显示的流量变为正值的方法简便、合理即可。如:改变通电线圈中电流的方向,使磁场B反向;或将传感器输出端对调接入显示仪表
(3)传感器和显示仪表构成闭合电路,由闭合电路欧姆定律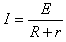
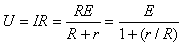
输入显示仪表的是a、c间的电压U,流量示数和U一一对应。E与液体电阻率无关,而r随电阻率的变化而变化,由③式可看出,r变化相应地U也随之变化。在实际流量不变的情况下,仪表显示的流量示数会随a、c间的电压U的变化而变化,增大R,使R>>r,则U≈E,这样就可以降低液体电阻率变化对显示仪表流量示数的影响
本题解析:
本题难度:困难
3、选择题 如图所示,半圆形光滑槽固定在地面上,匀强磁场与槽所形成的轨道平面垂直.将质量为m的带电小球自槽顶A处由静止释放,小球到达槽最低点C时,恰对槽无压力,则小球在以后的运动过程中对C点的最大压力为( )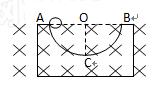
A.零
B.2mg
C.4mg
D.6mg
参考答案:D
本题解析:略
本题难度:一般
4、简答题 如图所示,质量为3.0kg的小车以1.0m/s的速度在光滑的水平面上向左运动,车上AD部分是表面粗糙的水平轨道,DC部分是1/4光滑圆弧,整个轨道都是由绝缘材料制成的,小车所在空间内有竖直向上的匀强电场和垂直纸面向里的匀强磁场,电场强度E为40N/C,磁感应强度B为2.0T。现有一质量为1.0kg、带负电且电荷量为 的滑块以8m/s的水平速度向右冲上小车,当它通过D点时速度为5.0m/s(滑块可视为质点,g取
的滑块以8m/s的水平速度向右冲上小车,当它通过D点时速度为5.0m/s(滑块可视为质点,g取 ),求:(计算结果保留两位有效数字)
),求:(计算结果保留两位有效数字)
(1)滑块从A到D的过程中,小车、滑块组成的系统损失的机械能;
(2)如果圆弧轨道半径为1.0m,求滑块刚过D点时对轨道的压力;
(3)若滑块通过D点时,立即撤去磁场,要使滑块不冲出圆弧轨道,此圆弧的最小半径。
参考答案:(1)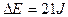 ?(2)
?(2)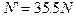 ?(3)0.90m
?(3)0.90m
本题解析:(1)(6分)设滑块运动到D点时的速度为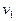 ,小车在此时的速度为
,小车在此时的速度为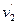
滑块从A运动到D的过程中系统动量守恒?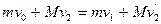 ? 2分
? 2分
小车的速度为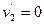
小车与滑块组成的系统损失的机械能为△E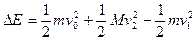 ? 2分
? 2分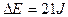 ? 2分
? 2分
(2)(6分)设滑块刚过D点时,受到轨道的支持力为N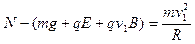 ? 4分
? 4分
得N="35.5N?" 1分
滑块对轨道压力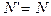 ?
?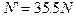 ? 1分
? 1分
(3)(8分)滑块沿圆弧轨道上升到最大高度时,滑块与小车具有共同速度v
由动量守恒定律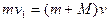 ? 2分
? 2分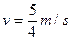 ? 2分
? 2分
设圆弧轨道的最小半径为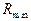
由动量守恒关系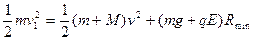 ? 2分
? 2分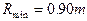 ? 2分
? 2分
本题难度:一般
5、选择题 磁流体发电是一项新兴技术,它可以把气体的内能直接转化为电能,如图是它示意图。平行金属板A、B之间有一个很强的匀强磁场,磁感应强度为B,将一束等离子体(即高温下电离的气体,含有大量正、负带电凿子)垂直于B的方向喷入磁场,每个离子的速度为v,电荷量大小为q,A、B两板间距为d,稳定时下列说法中正确的是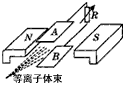
[? ]
A.图中A板是电源的正极
B.图中B板是电源的正极
C.电源的电动势为Bvd
D.电源的电动势为Bvq
参考答案:BC
本题解析:
本题难度:一般