时间:2020-08-15 23:23:26
1、计算题 光滑水平面上放着质量，mA＝1kg的物块A与质量mB＝2kg的物块B，A与B均可视为质点，A靠在竖直墙壁上，A、B间夹一个被压缩的轻弹簧（弹簧与A、B均不拴接），用手挡住B 不动，此时弹簧弹性势能EP＝49J。在A、B间系一轻质细绳，细绳长度大于弹簧的自然长度，如图所示。放手后B向右运动，绳在短暂时间内被拉断，之后B冲上与水平面相切的竖直半圆光滑轨道，其半径R＝0.5m，B恰能到达最高点C。g＝10m/s2，求
（1）绳拉断后瞬间B的速度vB的大小；
（2）绳拉断过程绳对B的冲量I的大小；
（3）绳拉断过程绳对A所做的功W。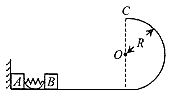 
参考答案：解：（1）设B在绳被拉断后瞬间和速度为vB，到达C点时的速度为vC，有
mBg＝mB
① 
mBv
＝
mB
＋2mBgR ②
代入数据得vB＝5m/s ③
（2）设弹簧恢复到自然长度时B的速度为v1，取水平向右为正方向，有
EP＝
mB
?④
I＝mBvB－mBv1 ⑤
代入数据得I＝－4N·s，其大小为4N·s ⑥
（3）设绳断后A的速度为vA，取水平向右为正方向，有
mBv1＝mBvB＋mAvA ⑦
W＝
mA
?⑧
代入数据得W＝8J ⑨
本题解析：
本题难度：困难
2、选择题 
物体A．B用轻绳连接，A上端与一个轻弹簧相连，弹簧上端固定在铁架台上，如图所示。已知两物体的质量分别是mA和mB, 开始时系统处于静止状态。现剪断连接A．B的细线，则B将自由下落，而A则在竖直方向做简谐运动。在B物体落到地面前的过程中，下面的说法中正确的是：
A．A．B组成的系统动量守恒
B．A物体的动量变化与B物体的动量变化大小相等、方向相反
C．弹簧弹力对物体A的冲量等于物体A的动量的增量
D．弹簧弹力对物体A的冲量等于重力对A．B的冲量之和再加上A．B的动量的增加量
参考答案：D
本题解析：
A．B组成的系统受到重力、弹簧的弹力作用，不满足动量守恒的条件，A．B不对而选项D正确。对物体A来说，弹簧弹力与重力的冲量的矢量和等于它动量的增量。
本题难度：简单
3、选择题 将质量为m0的木块固定在光滑水平面上，一颗质量为m的子弹以速度v0沿水平方向射入木块，子弹射穿木块时的速度为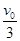
。现将同样的木块放在光滑的水平桌面上，相同的子弹仍以速度v0沿水平方向射入木块，设子弹在木块中所受阻力不变，则以下说法正确的是?（?）
A．若m0=3m，则能够射穿木块
B．若m0=3m，子弹不能射穿木块，将留在木块中，一起以共同的速度做匀速运动
C．若m0=3m，子弹刚好能射穿木块，此时子弹相对于木块的速度为零
D．若子弹以3v0速度射向木块，并从木块中穿出，木块获得的速度为v1；若子弹以4v0速度射向木块，木块获得的速度为v2；则必有v1＜v2
参考答案：B
本题解析：A、B、C、木块固定时，子弹射穿木块，设木块长度为d，根据功能关系，有fd=
m-m
,Q=m
-m故fd=Q=
,即f=
①
木块不固定时，子弹射入木块，系统动量守恒，假设不能穿出；
根据动量守恒定律，有mv0=（M+m）v根据功能关系，有Q′=fx=m-(M+m)v2
据题意，有：M=3m解得x=
?②
将①式代入②式，得到x=
故假设成立，子弹不能射出；
D、木块不固定时，子弹以速度v′射入木块，系统动量守恒，假设不能穿出；根据动量守恒定律，有mv′=（M+m）v
根据功能关系，有Q′="fx=" m
-(M+m)v2
据题意，有：M=3m,解得x=
③
将①式代入③式，得到x=
故当子弹以3v0速度或者4v0速度射向木块时，有x＞d，故子弹均射出；子弹初速度越大，穿出时间越短，木块加速时间越短，获得的速度越小.
本题关键是对子弹射穿木块过程运用动量守恒和功能关系联立方程求解，然后对结果进行讨论．
本题难度：一般
4、计算题 （16分）如图所示，在倾角为θ=37°的足够长的固定斜面上，物体A和小车B正沿着斜面上滑，A的质量为mA=0．50kg，B的质量为mB=0．25kg，A始终受到沿斜面向上的恒力F的作用．当A追上B时，A的速度为vA=1．8m/s，方向沿斜面向上，B的速度恰好为零，A、B相碰，相互作用时间极短，相互作用力很大，碰撞后的瞬间，A的速度变为v1=0．6m/s，方向沿斜面向上．再经T=0．6s，A的速度大小变为v2=1．8m/s，在这一段时间内A、B没有再次相碰．已知A与斜面间的动摩擦因数μ=0．15，B与斜面间的摩擦力不计，已知：sin37°=0．6，重力加速度g=10m/s2，求：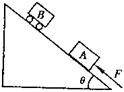
（1）A、B第一次碰撞后B的速度；方向沿斜面向上
（2）恒力F的大小．
参考答案：（1）vB=2．4m/s，
（2）F=0．6N
本题解析：（1）A、B碰撞过程中满足动量守恒，mAvA=mAv1+mBvB（2分）
得vB=2．4m/s（2分）
方向沿斜面向上（1分）
（2）设经过时间T=0．60s，A的速度方向向上，此时A的位移
m（1
分）
B的加速度aB=gsinθ=6m/s2（1分）
B的位移
m（1分）
可见A、B将再次相碰，违反了题意，因此碰撞后A先做匀减速运动，速度减为零后，
再做匀加速运动．（1分）
对A列出牛顿第二定律：mAgsinθ+μmgcosθ－F=mAa1，（2分）
mAgsinθ－μmgcosθ－F=mAa2，（2分）
v1=a1t1，v2=a2(T－t1) （2分）
解得F=0．6N（1分）
本题难度：简单
5、计算题 如图所示，A、B两球放在光滑的水平面上，水平面的右侧与竖直平面内一光滑曲面相切，现给A一向右的速度，让A与B发生对心弹性碰撞，小球沿曲面上升到最高点后又能再沿曲面滑回到水平面。若要B返回水平面时能再与么发生碰撞， A、B的质量应满足什么关系？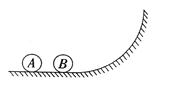
参考答案：mA＞mB/3
本题解析：设AB的质量分别为mAmB,设A的初速度为v0,当AB发生碰撞时有：
，
解得
，
若二者碰撞后都向右运动或A停止运动，是一定能发生第二次碰撞的，在碰后A向左运动时，要能发生二次碰撞需有
，解得mA＞mB/3
本题难度：一般