时间:2020-08-15 23:23:26
1、选择题 如图所示为半径很大的光滑圆弧轨道上的一小段,小球B静止在圆弧轨道的最低点O处,另有一小球A自圆弧轨道上C处由静止滚下,经过时间t?与B发生正碰,碰后两球分别沿相反方向在这段圆弧轨道上运动而未离开轨道.当两球第二次相碰时( )
A.所经过的时间为4t
B.所经过的时间为2t
C.将仍在O处相碰
D.可能在O点以外的其他地方相碰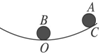
参考答案:因为他是一个很大的光滑圆弧上,这样的话可以当作一个单摆运动.
所以AB球发生正碰后各自做单摆运动.
T=2π
本题解析:
本题难度:一般
2、计算题 如图所示,光滑水平地面上有一足够长的木板,左端放置可视为质点的物体,其质量为m1=1kg,木板与物体间动摩擦因数μ=0.1。二者以相同的初速度v0=0.8m/s一起向右运动,木板与竖直墙碰撞时间极短,且没有机械能损失,g=10m/s2。如果木板质量m2=3kg,求物体相对木板滑动的最大距离;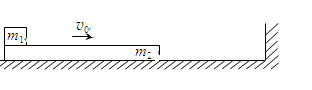
参考答案:L=0.96m
本题解析:木板与墙碰撞后,原速反弹,由动量守恒 (2分)
(2分)
v = 0.4m/s,方向向左,不会与竖直墙再次碰撞 (2分)
由能量守恒 (3分)
(3分)
解得 L=0.96m (2分)
考点:考查了动量守恒定律的应用
点评:本题是一道考查动量守恒和匀变速直线运动规律的过程复杂的好题,正确分析出运动规律是关键.
本题难度:一般
3、计算题 (10分)如图8—7—6,在水平地面上放置一质量为M的木块,一质量为m的子弹以水平速度v射入木块(未穿出),若木块与地面间的动摩因数为μ.
求(1)子弹击中木块后与木块的共同速度 ;
(2)子弹射入木块后,木块在地面上前进的距离。 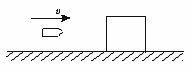
参考答案:
本题解析:在子弹射入木块的过程中子弹和木块组成的系统满足动量守恒,所以有:mv0=(m+M)v
可得子弹和木块的共同速度v= v0
v0
子弹射入木块后,以整体为研究对象,在地面滑行过程中有摩擦力对研究对象所做功等于此过程中整体动能的变化即:
-μ(m+M)gx=0- Mv2
Mv2
所以x=
本题难度:简单
4、填空题 如图所示,在光滑的水平面上有A、B两辆小车,水平面左侧有一竖直墙,在小车B上坐着一个小孩,小孩与B车的总质量是A车质量的10倍.两车从静止开始,小孩把A车以相对于地面的速度v推出,车A与墙碰撞后仍以原速度返回,小孩接到A车后,又把它以相对于地面的速度v推出.车A返回后,小孩再把它推出,每次推出,车A相对于地面的速度都是v,方向向左.则小孩把A车总共推出______次后,车A返回时,小孩不能再接到车.
参考答案:设小孩把A车总共推出n次后,车A返回时,小孩恰好不能再接到车.此时,车A返回时的速度v与B车的速度恰好相等.即vB=v ①
第1次推车时,小孩和B车获得的动量为mAv,以后每次推车时获得的动量为2mAv,根据动量守恒定律得
mAv+(n-1)?2mAv=2mBvB,②
又由题意,10mA=mB.③
联立①②③得:n=5.5
所以小孩把A车总共推出6次后,车A返回时,小孩不能再接到车.
故答案为:6
本题解析:
本题难度:一般
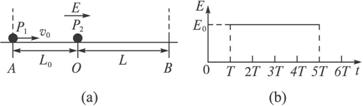
5、计算题 如图(a)所示,在光滑绝缘水平面的AB区域内存在水平向右的电场,电场强度E随时间的变化如图(b)所示.不带电的绝缘小球P2静止在O点.t=0时,带正电的小球P1以速度v0从A点进入AB区域,随后与P2发生正碰后反弹,反弹速度大小是碰前的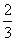 倍,P1的质量为m1,带电量为q,P2的质量m2=5m1,A,O间距为L0,O、B间距L=
倍,P1的质量为m1,带电量为q,P2的质量m2=5m1,A,O间距为L0,O、B间距L=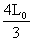 .已知
.已知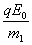 =
=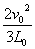 ,T=
,T=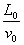 .
.
(1)求碰撞后小球P1向左运动的最大距离及所需时间.
(2)讨论两球能否在OB区间内再次发生碰撞.
参考答案:(1)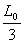 ,
,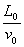 ? (2)能再次碰撞
? (2)能再次碰撞
本题解析:(1)P1经t1时间与P2碰撞,则t1=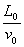 =T
=T
P1,P2碰撞,设碰后P2速度为v2,由动量守恒
m1v0=m1(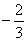 v0)+m2v2
v0)+m2v2
解得v2=v0/3(水平向右)
碰撞后小球P1向左运动的最大距离Sm=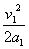
又a1=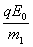 =
=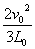
解得Sm=L0/3
所需时间t2=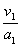 =
=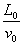 .
.
(2)P2从O点运动到B点所需时间t2=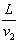 =4T
=4T
在t2时间内,一直存在电场,则P1的位移
x1=v1t2+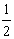 at22=2L
at22=2L
由于x1>L,故在OB之间P1与P2能再次碰撞.
本题难度:一般