时间:2020-08-09 23:12:25
1、选择题 物体先做初速度为零的匀加速运动,加速度大小为a1,当速度达到v时,改为以大小为a2的加速度做匀减速运动,直至速度为零,在加速和减速过程中物体的位移和所用时间分别为x1、t1和x2、t2,下列各式成立的是(?)
A.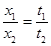
B.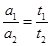
C.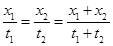
D.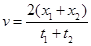
参考答案:ACD
本题解析:物体先做初速度为零的匀加速运动,后做匀减速运动,末速度为零,两个过程平均速度相等,匀加速运动的末速度与匀减速运动的初速度相同,运用位移公式和速度公式分别研究位移与时间、加速度与时间的关系.由速度位移关系式研究速度与位移的关系.对于整个运动过程,应用平均速度研究总位移与总时间的关系.
A、由题得到,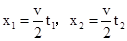 ,则两式相比得到,
,则两式相比得到,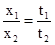 .故A正确.
.故A正确.
B、由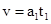 ,又
,又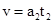 ,得到,
,得到,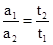 .故B错误.
.故B错误.
C、所以整个过程的平均速度也为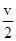 ,即
,即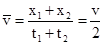 ,
,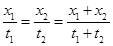 .故C正确.
.故C正确.
D、对于整个运动过程,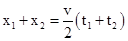 ,得到,
,得到,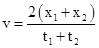 .故D正确.
.故D正确.
本题选错误的,故选ACD.
点评:本题关键对于两个运动过程之间的关系要熟悉,并能将这些关系转变成方程.中等难度,若基本扎实,不会出错.
本题难度:一般
2、选择题 如图所示,在一辆足够长的小车上,有质量为m1、m2的两个滑块(m1>m2)原来随车一起运动,两滑块与车接触面的动摩擦因数相同,当车突然停止后,则两个滑块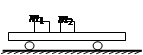
A.一定相碰
B.一定不相碰
C.若车原来向右运动,则可能相碰
D.若车原来向左运动,则可能相碰
参考答案:B
本题解析:若μ=0,当车突然停止时,两物块所受的合力为零,将以相同的速度做匀速直线运动,一定不会相撞;若μ≠0,当车突然停止时,两物块做匀减速运动,加速度a=μg,因为初速度相同,所以两滑块一定不相撞.故B正确。
本题难度:一般
3、简答题 如图所示,质量为m的金属块放在水平桌面上,在与水平方向成θ角斜向上、大小为F的拉力作用下,以速度v向右做匀速直线运动.重力加速度为g.
(1)求金属块与桌面间的动摩擦因数;
(2)如果从某时刻起撤去拉力,则撤去拉力后金属块在桌面上还能滑行多远?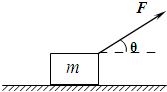
参考答案:(1)对金属块受力分析,受拉力、重力、支持力、摩擦力,如图所示: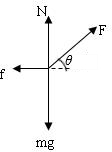
因为金属块匀速运动,受力平衡则有
Fcosθ-μ(mg-Fsinθ)=0
得μ=Fcosθmg-Fsinθ
(2)撤去拉力后金属块的加速度大小为:a=-fm=-μg=-Fgcosθmg-Fsinθ
金属块在桌面上滑行的最大距离:s=-v22a=v2(mg-Fsinθ)2Fgcosθ
答:(1)金属块与桌面间的动摩擦因数为Fcosθmg-Fsinθ;
(2)撤去拉力后金属块在桌面上滑行的最大距离为v2(mg-Fsinθ)2Fgcosθ.
本题解析:
本题难度:一般
4、选择题 一辆农用“小四轮”漏油了,假如车在平直的公路上行驶时每隔1s漏下一滴油.一位同学根据漏在路面上的油滴分布,分析“小四轮”的运动情况(已知车的运动方向不变).下列说法中正确的是( )
A.当沿运动方向油滴间距逐渐减小时,车一定在做匀减速直线运动
B.当沿运动方向油滴间距逐渐增大时,车可能在做匀加速直线运动
C.当沿运动方向油滴间距逐渐增大时,车一定在做匀加速直线运动
D.当沿运动方向油滴间距逐渐减小时,车可能在做匀减速直线运动.
参考答案:BD
本题解析:
本题难度:一般
5、计算题 (6分)一辆汽车在平直的公路上做匀变速直线运动,该公路每隔60米就有一电线杆,汽车通过第一根和第二根电线杆用了5秒,通过第二根和第三根电线杆用了3秒。求:汽车的加速度和经过第一根电线杆时的瞬时速度。
参考答案: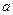 =2m/s2?
=2m/s2?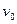 =7m/s
=7m/s
本题解析:由运动学公式得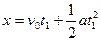 ①?(2分)
①?(2分) ②?(2分)
②?(2分)
将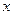 ="60m?"
="60m?" 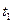 ="5s?"
="5s?" 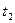 =8s代入①②得:
=8s代入①②得: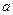 =2m/s2?
=2m/s2?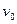 ="7m/s?" ?(2分)
="7m/s?" ?(2分)
本题难度:简单