时间:2019-12-13 01:56:09
1、计算题 一初速度为零的带电粒子从A板处经电压为U=4.0×103V的匀强电场加速后,到B板处获得5.0×103m/s的速度,粒子通过加速电场的时间t=1.0×10-4s,不计重力作用,
(1)带电粒子的比荷为多大?
(2)匀强电场的场强为多大?
(3)粒子通过电场过程中的位移为多
参考答案:(1)3.125×103C/㎏?(2)1.6×104V/m?(3)0.25m
本题解析:(1)由动能定理得: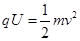
解得: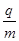 =3.125×103C/㎏
=3.125×103C/㎏
(2)粒子匀加速运动: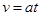
由牛顿第二定律得: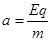
联立解得:E=1.6×104V/m
(3)由动能定理得: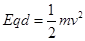
解得:d=0.25m
本题难度:一般
2、计算题 如图所示,一个质量为m,电荷量+q的带电微粒(重力忽略不计),从静止开始经U1电压加速后,水平进入两平行金属板间的偏转电场中,金属板长L,两板间距d,微粒射出偏转电场时的偏转角θ=30°,又接着进入一个方向垂直于纸面向里的匀强磁场区,求: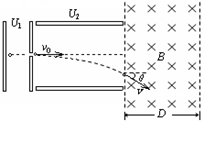
(1)微粒进入偏转电场时的速度v0是多大?
(2)两金属板间的电压U2是多大?
(3)若该匀强磁场的磁感应强度B,微粒在磁场中运动后能从左边界射出,则微粒在磁场中的运动时间为多少?
(4)若该匀强磁场的宽度为D,为使微粒不会从磁场右边射出,该匀强磁场的磁感应强度B至少多大?
参考答案:(1)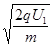 (2)
(2)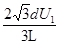 (3)
(3)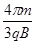 (4)
(4)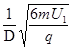
本题解析:
(1)由带电粒子经U1电压加速
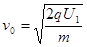
由带电粒子经U2电压偏转,可知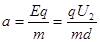
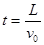
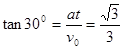
得 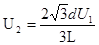
(3)带电粒子在磁场中运动,从左边界出,对应圆周运动的圆心角240º,由洛伦兹力提供向心力,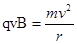
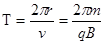
带电粒子在磁场中的时间: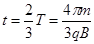
(4)微粒和右边界相切时,该匀强磁场的磁感应强度最小值为B0,设粒子进入磁场速度为vt,运动半径为R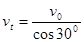
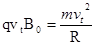
由几何关系得:R+Rsin300=D
求得: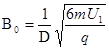
考点:带电粒子在匀强电场中的加速及在匀强磁场中的运动.
本题难度:困难
3、计算题 如图为伦琴射线管示意图,K为阴极钨丝,发射的电子初速度为零,A为对阴极(阳极),当A、K之间加直流电压U=30 kV时,电子被加速打在对阴极A上,使之发出X射线,设电子的动能全部转化为伦琴射线(X射线)的能量.求:?
(1)电子到达对阴极的速度多大??
(2)如果对阴极每吸收一个电子放出一个X射线光子,则当A、K之间的电流为10 mA时,每秒钟从对阴极最多辐射出多少个X射线光子?(电子质量m=0.91×10-30 kg,电荷量e=1.6×10-19 C)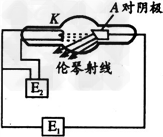
参考答案:解:(1)由动能定理,得: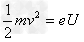
则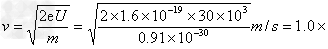 108m/s
108m/s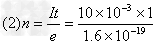 个=6.25×1016 个
个=6.25×1016 个
本题解析:
本题难度:一般
4、选择题 距离足够大的金属板A、B间有一电子(不计重力影响),在A、B间接有如图所示的正弦式电压u,t=0时电子从静止开始运动,则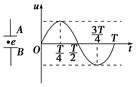
A.电子做往复运动
B.在足够长的时间后,电子一定要碰到某个金属板上
C.t=T/2时,电子速度达到最大值
D.t=T时,电子将回到原出发点
参考答案:BC
本题解析:电子在前半个周期内,电场力做正功,粒子做加速运动,t=T/2时速度最大,在后半个周期内,电场方向变成反向,则电子做减速运动,t=T时,速度为零,如此循环电子始终朝一个方向运动,不断交替加速、减速,所以电子做单方向运动,一定会在某个时间碰到极板,AD错误,BC正确,
故选BC.
点评:本题的关键是判断清楚粒子不是做往返运动,而是做单向直线运动
本题难度:一般
5、计算题 如图所示,两平行金属板相距为d,加上如图所示(b)所示的方波形电压,电压的最大值为U0,周期为T.现有重力可忽略的一束离子,每个离子的质量为m,电量为q,从与两板等距处的O点,沿着与板平行的方向连续地射入两板中。已知每个离子通过平行板所需的时间恰为T(电压变化周期)且所有离子都能通过两板间的空间,打在两金属板右端的荧光屏上,试求: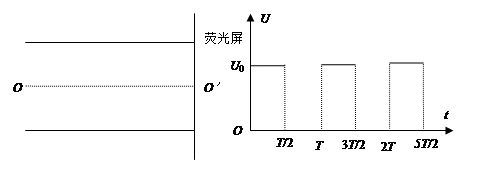
(1)离子打在荧光屏上的位置与O′点的最小距离
(2)离子打在荧光屏上的位置与O′点的最大距离。
参考答案:(1) 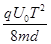 ;(2)
;(2)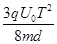
本题解析:
试题分析: 在T/2、3T/2……等时刻进入的粒子,前T/2时间做匀速直线运动,后T/2做类平抛运动,垂直金属板方向的位移最小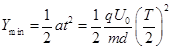 =
=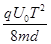
在0、T、2T、3T……等时刻进入的粒子,前T/2时间做类平抛运动,后T/2做匀速直线运动,位移最大
第T/2时垂直金属板方向的速度 V=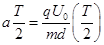
前T/2时垂直金属板方向的位移 Y1=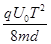
后T/2时垂直金属板方向的位移Y2="V" 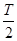 =
=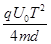
离子在垂直金属板方向的总位移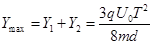
时间内,在水平方向上做匀速直线运动,在竖直方向上做匀加速直线运动,竖直方向的位移为
本题难度:一般