时间:2019-07-03 00:19:37
1、选择题 如图所示，固定曲面AC是一段半径为4.0米的光滑圆弧形成的，圆弧与水平方向相切于A点，AB＝10cm，现将一小物体先后从圆弧顶端C和中点D处由静止释放，到达曲面低端时速度分别为v1和v2，所需时间为t1和t2，以下说法正确的是(? )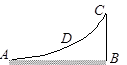
A．v1 > v2 , t1＝ t2
B．v1 > v2 , t1 > t2
C．v1 < v2 , t1＝ t2
D．v1 < v2 , t1 > t2
参考答案：A
本题解析：将小物体沿圆弧的运动等效成单摆，其摆长等于圆弧的半径，由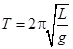
可知从D点释放和从C释放到底端的时间均为四分之一周期，所以时间相等即t1＝ t?2；由机械能守恒定律
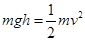可知v1 > v2，故选项A正确．
本题难度：一般
2、计算题 如图所示，总长为L的光滑均匀铁链，跨过一个轻质小滑轮，开始时底端相平，当略有扰动时其一端下沉，试求铁链刚脱离滑轮的速度大小。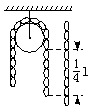
参考答案：解：取整个铁链为研究对象，铁链由开始运动到脱离滑轮的过程中，重心下降了L/4，由机械能守恒定律得ΔEk=－ΔEp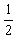
mv2=mg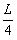
v=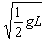
本题解析：
本题难度：一般
3、填空题 （1）如图甲所示，是用包有白纸的质量为1.00kg的圆柱棒替代纸带和重物，蘸有颜料的毛笔固定在电动机的飞轮上并随之匀速转动，以替代打点计时器。烧断悬挂圆柱棒的线后，圆柱棒竖直自由下落，毛笔就在圆柱棒面的纸上画出记号（如图乙所示）。设毛笔接触棒时不影响棒的运动，测得记号之间的距离依次为26.0 mm、50.0 mm、74.0mm、98.0 mm、122.0 mm、146.0 mm，由此可验证机械能守恒定律．已知电动机铭牌上标有“1200 r／min”字样．根据以上内容回答下列问题．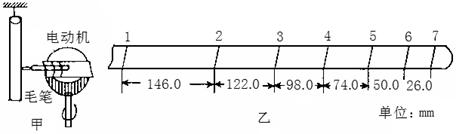
①毛笔画相邻两条线的时间间隔T=?s．
②根据图乙所给的数据可知：毛笔画下记号“3”时，圆柱棒下落的速度V3=?m/s；画下记号“6”时，圆柱棒下落的速度V6=?m/s；在毛笔画下记号“3到画下记号“6”的这段时间内，棒的动能的变化量为
?J，重力势能的变化量为?J．由此可得出的结论是：?。
(g取9.8m/s2,结果保留三位有效数字)
参考答案：①0.05s?②v3=2.20m/s? v6=0.760m/s? 2.13J? 2.18J?在误差范围内，减小的重力势能等于增加的动能，机械能守恒
本题解析：①毛笔随电动机转动的转速为n=1200r/min=20r/s，周期T=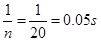
②因两相邻记号时间间隔相等，所以毛笔画下记号“3”时，圆柱棒下落的速度V3为记号2、4间平均速度，由平均速度公式得V3=
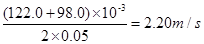，同理画下记号“6”时，圆柱棒下落的速度V6=
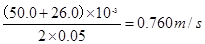，在毛笔画下记号“3到画下记号“6”的这段时间内，棒的动能的变化量为
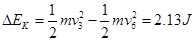，重力势能的变化量为
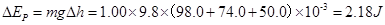，因
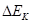近似等于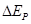
，由此得出的结论是在误差范围内，减小的重力势能等于增加的动能，即机械能守恒
本题难度：一般
4、计算题 如图所示为火车站装载货物的原理示意图。设AB段是距水平传送带装置高为H=5m的光滑斜面，水平段BC使用水平传送带装置，BC长L=8m，与货物的动摩擦因数为μ=0.6，皮带轮的半径为R=0.2m，上部距车厢底水平面的高度h=0.45m设货物由静止开始从A点下滑，经过B点的拐角处无机械能损失，通过调整皮带轮（不打滑）的转动角速度ω可使货物经C点抛出后落在车厢上的不同位置，取g=10m/s2，求：
（1）当皮带轮静止时，货物在车厢内的落地点到C点的水平距离；
（2）当皮带轮以角速度ω=20rad/s顺时针方向匀速转动时，货物在车厢内的落地点到C点的水平距离；
（3）试写出货物在车厢内的落地点到C点的水平距离s随皮带轮角速度ω变化关系，并画出s-ω图象。（设皮带轮顺时针方向转动时，角速度ω取正值，水平距离向右取正值)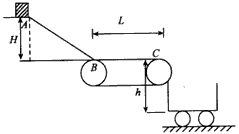 
? 
参考答案：解：设货物在B点的速度为v0，由机械能守恒定律可得：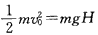
得：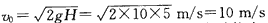
（1）货物从B到C做匀减速运动，由动能定理得：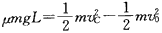
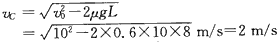
落地点到C点的水平距离：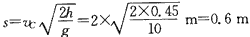
（2）皮带速度：v皮=ω·R=20×0.2m/s=4m/s
结合（1）可知，货物先减速运动，当速度减小为4m/s时开始做匀速运动，最后从C点抛出，落地点到C点的水平距离：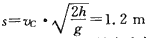
（3）①皮带轮逆时针方向转动：
无论角速度为多大，货物从B到C均做匀减速运动，在C点的速度为vC=2 m/s，落地点到C点的水平距离s=0.6m
②皮带轮顺时针方向转动时：
I．当0≤ω≤10 rad/s时：s=0.6 m
Ⅱ．当10＜ω≤50 rad/s时：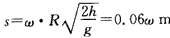
Ⅲ．当50＜ω＜70 rad/s时：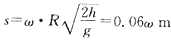
Ⅳ．当ω≥70 rad/s时：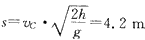
?s-ω图象如图所示：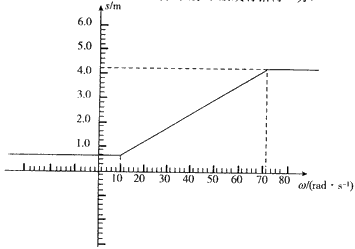
本题解析：
本题难度：困难
5、计算题 用长L=1.6m的细绳，一端系着质量M=1kg的木块，另一端挂在固定点上。现有一颗质量m=20g的子弹以v1=500m／s的水平速度向木块中心射击，结果子弹穿出木块后以v2=100m／s的速度前进。问木块能运动到多高？（取g=10m／s2，空气阻力不计）
参考答案：2.96m
本题解析：
【错解分析】错解：在水平方向动量守恒，有
mv1=Mv+mv2? (1)
式①中v为木块被子弹击中后的速度。木块被子弹击中后便以速度v开始摆动。由于绳子对木块的拉力跟木块的位移垂直，对木块不做功，所以木块的机械能守恒，即
?（2）
h为木块所摆动的高度。解①，②联立方程组得到
v=8(m/s)
h=3.2(m)
【错解原因】这个解法是错误的。h=3.2m，就是木块摆动到了B点。如图所示。则它在B点时的速度vB。应满足方程
这时木块的重力提供了木块在B点做圆周运动所需要的向心力。解上述方程得
（m/s）
如果vB＜4 m/s，则木块不能升到B点，在到达B点之前的某一位置以某一速度开始做斜向上抛运动。而木块在B点时的速度vB=4m/s，是不符合机械能守恒定律的，木块在 B点时的能量为(选A点为零势能点)
木块在A点时的能量为
两者不相等。可见木块升不到B点，一定是h＜3.2 m。
实际上，在木块向上运动的过程中，速度逐渐减小。当木块运动到某一临界位置C时，如图所示，木块所受的重力在绳子方向的分力恰好等于木块做圆周运动所需要的向心力。此时绳子的拉力为零，绳子便开始松弛了。木块就从这个位置开始，以此刻所具有的速度vc作斜上抛运动。木块所能到达的高度就是C点的高度和从C点开始的斜上抛运动的最大高度之和。
【正解】如上分析，从式①求得vA=v=8m/s。木块在临界位置C时的速度为vc，高度为
h′=l(1+cosθ)?如图所示，
根据机船能守恒定律有
?③
又
，即
?④
从式③和式④得
所以
木块从C点开始以速度vc做斜上抛运动所能达到的最大高度h″为
所以木块能达到的最大高度h为
【点评】物体能否做圆运动，不是我们想象它怎样就怎样这里有一个需要的向心力和提供向心力能否吻合的问题，当需要能从实际提供中找到时，就可以做圆运动。所谓需要就是符合牛顿第二定律F向=ma向的力，而提供则是实际中的力若两者不相等，则物体将做向心运动或者离心运动。
本题难度：一般