时间:2019-07-03 00:05:04
1、计算题 (15分)某校举行托乒乓球跑步比赛，赛道为水平直道，比赛距离为s，比赛时，某同学将球置于球拍中心，以大小为a的加速度从静止开始做匀加速直线运动，当速度达到v0时，再以v0做匀速直线运动跑至终点，整个过程中球一直保持在球拍中心不动，比赛中，该同学在匀速直线运动阶段保持球拍的倾角为θ0，如图所示，设球在运动中受到空气阻力大小与其速度大小成正比，方向与运动方向相反，不计球与球拍之间的摩擦，球的质量为m，重力加速度为g。求：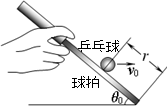
⑴空气阻力大小与球速大小的比例系数k；
⑵加速跑阶段球拍倾角θ随速度v变化的关系式；
⑶整个匀速跑阶段，若该同学速度仍为v0，而球拍的倾角比θ0大了β并保持不变，不计球在球拍上的移动引起的空气阻力变化，为保证到达终点前球不从球拍上距离中心为r的下边沿掉落，求β应满足的条件。
参考答案：⑴k＝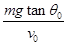
；⑵tanθ＝
＋
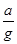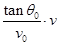；⑶sinβ≤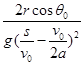
本题解析：⑴在匀速运动阶段，球受重力mg、球拍的支持力N0，和空气阻力f0作用，根据共点力平衡条件有：f0＝mgtanθ0?①
根据题意有：f0＝kv0?②
由①②两式联立解得：k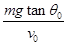＝?③
⑵在加速阶段，球受重力mg、球拍的支持力N，和空气阻力f作用，在竖直方向上有：Ncosθ＝mg ④
在水平方向上，根据牛顿第二定律有：Nsinθ－f＝ma?⑤
根据题意有：f＝kv?⑥
由③④⑤⑥式联立解得：tanθ＝＋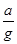
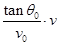
⑶以速度v0匀速运动，而球拍的倾角为θ0＋β，并保持不变时，设空气阻力f0与重力mg的合力为F，方向仍然与水平方向成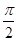
－θ0斜向后下方，因此有：F＝
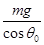?⑦
设球沿球拍面下滑的加速度大小为a′，根据牛顿第二定律有：Fsinβ＝ma′?⑧
设匀加速运动的位移为s1，根据匀变速直线运动规律有：s1＝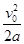
?⑨
根据几何关系可知，匀速运动的位移为：s2＝s－s1?⑩
根据匀速运动规律可知，匀速运动阶段的时间为：t＝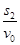
?
球不从球拍上距离中心为r的下边沿掉落的条件为：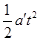
≤r?
由⑦⑧⑨⑩?式联立解得：sinβ≤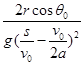
本题难度：一般
2、选择题 一个物体在直线上以恒定的加速度运动，它的位移与时间的关系是s=8t-4t2，则此物体（ ）
A．初速度为8m/s，加速度大小为4m/s2，作匀减速直线运动
B．初速度为8m/s，加速度大小为8m/s2，作匀减速直线运动
C．物体3s内的位移大小为4m，3s末的速度大小为0m/s
D．物体3s内的位移大小为12m，3s末的速度大小为16m/s
参考答案：AB、根据匀变速直线运动的位移时间关系有x=v0t+12at2与s=8t-4t2
对比可以知道
v0=8m/s，加速度a=-8m/s2，加速度和速度反向，物体做匀减速运动，所以错误，B正确．
由s=8t-4t2知当t=3s时，s=8×3-4×32m=-12m
由v=v0+at=8-8×3=-16m/s，故大小为16m/s，方向与初速度反向．
故选：BD．
本题解析：
本题难度：一般
3、选择题 甲乙两辆汽车在平直的公路上沿同一方向做直线运动，t=0时刻同时经过公路旁的同一路标．在如图描述两车运动的v-t图中，直线a、b分别描述了甲乙两车在0～20秒的运动情况．关于两车之间的位置关系，下列说法正确的是（ ）
A．在0～10秒内两车逐渐靠近
B．在10～20秒内两车逐渐远离
C．在t=10秒时两车在公路上相遇
D．在5～15秒内两车的位移相等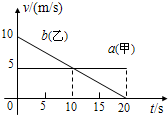
参考答案：
A、在0～10秒内，乙车在甲的前方，而且乙的速度大于甲的速度，则两车逐渐远离；故A错误．
B、在10～20秒内，乙车在甲的前方，乙的速度小于甲的速度，则两车逐渐靠近．故B错误．
C、根据图象的“面积”等于物体的位移大小，可以看出，在t=10秒时乙车的位移大于甲车的位移，t=0时刻又在同一位置出发，所以在t=10秒时两车没有相遇．故C错误．
D、在5～15秒内两车图线的“面积”相等，则通过的位移相等．故D正确．
故选D
本题解析：
本题难度：一般
4、选择题 飞机着陆后做匀减速运动，初速度是60m/s，加速度的大小为10m/s2，则飞机着陆后8s内的位移是（ ）
A．160m
B．180m
C．240m
D．300m
参考答案：由速度公式可得，火车减速到零所用的时间t=0-60-10=6s；
故8s内的位移为6s内的位移，则有v2-v02=2ax可得：
x=6022×10=180m；
故选B．
本题解析：
本题难度：简单
5、简答题 如图所示，水平轨道AB与放置在竖直平面内的1/4圆弧轨道BC相连，圆弧轨道的B端的切线沿水平方向．一质量m=1.0kg的滑块（可视为质点），在水平恒力F=5.0N的作用下，从A点由静止开始运动，已知A、B之间的距离s=5.5m，滑块与水平轨道间的动摩擦因数μ=0.10，圆弧轨道的半径R=0.30m，取g=10m/s2．
（1）求当滑块运动的位移为2.0m时的速度大小；
（2）当滑块运动的位移为2.0m?时撤去F，求滑块通过B点时对圆弧轨道的压力大小；
（3）滑块运动的位移为2.0m时撤去F后，若滑块恰好能上升到圆弧轨道的最高点，求在圆弧轨道上滑块克服摩擦力所做的功．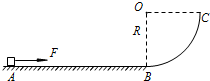
参考答案：（1）设滑块的加速度为a1，根据牛顿第二定律
F-μmg=ma1
解得：a1=4.0m/s2
设滑块运动的位移为2.0m时的速度大小为v，根据运动学公式
v2=2a1s1
解得：v=4.0m/s
（2）设撤去拉力F后的加速度为a2，根据牛顿第二定律
μmg=ma2
解得：a2=μg=1.0m/s2
设滑块通过B点时的速度大小为vB，根据运动学公式
v2B-v2=-2a2(S-S1)
解得：vB=3.0m/s
设滑块在B点受到的支持力为NB，根据牛顿第二定律
NB-mg=mv2BR
解得：NB=40N
根据牛顿第三定律，滑块通过B点时对圆弧轨道的压力为40N．
（3）设圆弧轨道的摩擦力对滑块做功为W，根据动能定理
-mgR+W=0-12mv2B
解得：W=-1.5J
圆弧轨道上滑块克服摩擦力所做的功为1.5J．
答：（1）求当滑块运动的位移为2.0m时的速度大小为4.0m/s；
（2）当滑块运动的位移为2.0m 时撤去F，滑块通过B点时对圆弧轨道的压力大小为40N；
（3）滑块运动的位移为2.0m时撤去F后，若滑块恰好能上升到圆弧轨道的最高点，在圆弧轨道上滑块克服摩擦力所做的功为1.5J．
本题解析：
本题难度：一般