时间:2019-07-02 23:55:49
1、选择题 质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直放置,开口向上,滑到最低点时速度大小为V,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )
A.受到向心力为mg+m
| v2 R |
| v2 R |
2、选择题 如图所示,在方向竖直向下的匀强电场中,用绝缘细线拴着带负电的小球(视为质点)在竖直平面内绕O点做圆周运动,则下列判断正确的是( )
A.小球运动到最低点时,细线的拉力一定最大
B.小球运动到最低点时,小球的速度一定最大
C.小球运动到最高点时,小球的动能一定最小
D.小球运动到最高点时,小球的机械能一定最大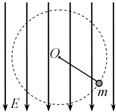
3、选择题 从2007年4月18日起,全国铁路正式实施第六次大面积提速,时速将达到200公里以上,其中京哈、京沪、京广、胶济等提速干线的部分区段时速可达250公里,我们从济南到青岛乘“和谐号”列车就可以体验时速250公里的追风感觉.火车转弯可以看成是在水平面内做匀速圆周运动,火车速度提高会使外轨受损.为解决火车高速转弯时外轨受损这一难题,你认为以下措施可行的是( )
A.适当减小内外轨的高度差
B.适当增加内外轨的高度差
C.适当减小弯道半径
D.适当增大弯道半径
4、选择题 不定项选择
下列说法中正确的是( ? )
A.向心加速度是描述角速度变化的快慢的物理量
B.向心加速度是描述线速度大小变化的快慢的物理量
C.向心加速度总是与速度方向垂直
D.向心加速度只改变速度的方向
5、选择题 关于向心力,下列说法中正确的是
[? ]
A.物体由于做圆周运动而产生了向心力
B.向心力不改变圆周运动物体的速度
C.做匀速圆周运动的物体其向心力是不变的
D.做匀速圆周运动的物体其向心力为物体所受的合外力