时间:2019-06-29 05:54:03
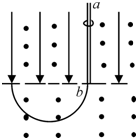
1、简答题 如图所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感应强度相同的匀强磁场,方向垂直纸面向外,ab是一根长为l的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上,将一套在杆上的带正电的小球从a端由静止释放后,小球先作加速运动,后作匀速运动到达b端,已知小球与绝缘杆间的动摩擦系数μ=0.3,小球重力忽略不计,当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆的半径是
| l 3 |
参考答案: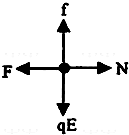
小球在沿杆向下运动时,受力情况如图,向左的洛仑兹力F,向右的弹力N,向下的电场力qE,向上的摩擦力f
F=Bqv,N=F=Bqv?
∴f=μN=μBqv
当小球作匀速运动时,qE=f=μBqVb
小球在磁场中作匀速圆周运动时?Bqvb=mV2bR
又R=l3,
∴vb=Bql3m
小球从a运动到b过程中,
由动能定理得W电-Wf=mv2b2-0
W电=qEl=μBqVbl=B2q2l210m
所以Wf=W电-mv2b2=B2q2l210m-mB2q2l22×9m2=2B2q2l245m
WfW电=49
答:带电小球从a到b运动过程中克服摩擦力所做的功与电场力所做功的比值为49.
本题解析:
本题难度:一般
2、选择题 用一根细绳,一端系住一定质量的小球,小球大小忽略.另一端固定在天花板上,使小球做如图的匀速圆周运动.现在有如图5两个这样的装置(a)和(b),(a)、(b)图中,两球转动的角速度大小相同,绳与竖直方向的夹角分别为37°和53°.则a、b两球的转动半径Ra和Rb之比,以及相对应的绳子的长度La和Lb之比分别为:(sin37°=0.6;cos37°=0.8)( )
A.Ra:Rb=9:16;La:Lb=4:3
B.Ra:Rb=9:16;La:Lb=3:4
C.Ra:Rb=3:4;La:Lb=9:16
D.Ra:Rb=3:4;La:Lb=16:9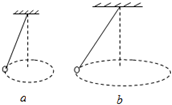
参考答案:小球所受的合力F合=mgtanθ=mrω2,则角速度的大小ω=
本题解析:
本题难度:一般
3、简答题 如图所示,已知半径分别为R和r(R>r)的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,甲轨道左侧又连接一个光滑的轨道,两圆形轨道之间由一条水平轨道CD相连.一小球自某一高度由静止滑下,先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开圆轨道.若小球在两圆轨道的最高点对轨道压力都恰好为零.试求:
(1)分别经过C、D时的速度;
(2)小球释放的高度h;
(3)水平CD段的长度.
参考答案:(1)小球在光滑圆轨道上滑行时,机械能守恒,设小球滑过C点时的速度为vc,通过甲环最高点速度为v′,根据小球对最高点压力为零,有
?mg=m?v′2R? ?①
取轨道最低点为零势能点,由机械守恒定律
?12mv2c=mg?2R+12mv′2?②
由①、②两式消去v′,可得
vc?=
本题解析:
本题难度:一般
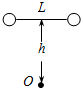
4、选择题 如图,两质量均为m的小球,通过长为L的不可伸长轻绳水平相连,从h高处自由下落,下落过程中绳处于水平伸直状态,若下落时绳中点碰到水平放置的光滑钉子O,绳与钉作用过程中无能量损失,重力加速度为g,则( )
A.小球从开始下落到刚到达最低点的过程中机械能守恒
B.从轻绳与钉子相碰到小球刚达到最低点过程,重力的功率先减小后增大
C.小球刚到最低点速度大小为
| 2g(h+L) |
| 4mgh L |
参考答案:A、小球从开始下落到刚到达最低点的过程中只有重力做功,机械能守恒,故A正确;
B、以向下为正方向,竖直方向合力为F=mg-Tsinθ,开始时θ很小,mg>Tsinθ,F>0,竖直方向加速度向下,vy增大,到快要相碰时,Tsinθ>mg,F<0,竖直方向加速度向上,vy减小,根据PG=mgvy可知重力的瞬时功率先增大后减小,故B错误;
C、从最高点到小球刚到达最低点的过程中运用动能定理得:12mv2=mg(L2+h),解得:v=
本题解析:
本题难度:简单
5、计算题 用一根长L=0.8 m的轻绳,吊一质量为m=1.0 g的带电小球,放在磁感应强度B=0.1 T,方向如图所示的匀强磁场中,把小球拉到悬点的右端,轻绳刚好水平拉直,将小球由静止释放,小球便在垂直于磁场的竖直平面内摆动,当小球第一次摆到最低点时,悬线的拉力恰好为零(重力加速度g取10 m/s2)。试问:
(1)小球带何种电荷?电量为多少?
(2)当小球第二次经过最低点时,悬线对小球的拉力多大? 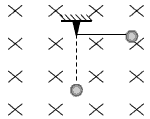
参考答案:解:(1)设小球第一次到达最低点速度为v,则由动能定理可得: 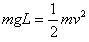
在最低点由圆周运动规律得: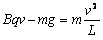
解得q=7.5×10-2 C,带负电
(2)小球第二次到达最低点速度仍为v,由圆周运动规律得: 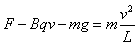
解得F=0.06 N
本题解析:
本题难度:一般