时间:2019-06-26 04:11:38
1、选择题 如图所示为一理想变压器,原、副线圈的匝数比为n.原线圈接电压为u=U0sinωt的正弦交流电,输出端接有一个交流电流表和一个电动机,电动机的线圈电阻为R.当输入端接通电源后,电动机带动一质量为m的重物匀速上升,此时电流表的示数为I,重力加速度为g,下列说法正确的是( )
A.电动机两端电压为IR
B.原线圈中的电流为nI
C.电动机消耗的电功率为U0I/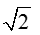 n
n
D.重物匀速上升的速度为I(U0-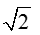 nIR)/
nIR)/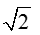 nmg
nmg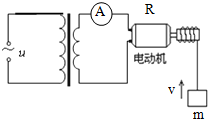
参考答案:CD
本题解析:
本题难度:一般
2、选择题 在竖直向下的匀强磁场中,将一水平放置的金属棒AB,以初速度v水平抛出。空气阻力不计,如图,运动过程中棒保持水平,那么下列说法中正确的是( ? )

参考答案:B
本题解析:
本题难度:一般
3、选择题 如图所示,两光滑平行金属导轨间距为L,直导线MN垂直跨在导轨上,且与导轨接触良好,整个装置处于垂直纸面向里的匀强磁场中,磁感应强度为B,电容器的电容为C,除电阻R外,导轨和导线的电阻均不计.现给导线MN一初速度,使导线MN向右运动,当电路稳定后,MN以速度v向右做匀速运动,则? 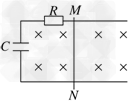
[? ]
A.电容器两端的电压为零
B.电阻两端的电压为BLv
C.电容器所带电荷量为CBLv
D.为保持MN匀速运动,需对其施加的拉力大小为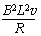
参考答案:C
本题解析:
本题难度:一般
4、计算题 (18分)
如图所示,倾斜角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接.轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T;匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=1T.现将两质量均为m=0.2kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放.取g=10m/s2.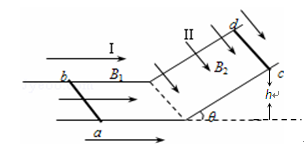
(1)求导体棒cd沿斜轨道下滑的最大速度的大小;
(2)若已知从开始运动到cd棒达到最大速度的过程中,ab棒产生的焦耳热Q=0.45J,求该过程中通过cd棒横截面的电荷量;
(3)若已知cd棒开始运动时距水平轨道高度h=10m,cd棒由静止释放后,为使cd棒中无感应电流,可让磁场Ⅱ的磁感应强度随时间变化,将cd棒开始运动的时刻记为t=0,此时磁场Ⅱ的磁感应强度为B0=1T,试求cd棒在倾斜轨道上下滑的这段时间内,磁场Ⅱ的磁感应强度B随时间t变化的关系式.
参考答案:(1)1m/s(2)1C(3)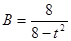 , (t<
, (t<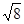 s)
s)
本题解析:(1)在cd从开始运动到达最大速度的过程中ab棒受到的安培力竖直向上,且mg>BIL,故ab棒处于静止状态。
cd棒匀速运动时速度最大,设为vm,棒中感应电动势为E,电流为I,
感应电动势:E=BLvm,电流: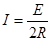 (2分)
(2分)
由平衡条件得:mgsinθ=BIL,代入数据解得:vm=1m/s;(2分)
(2)在cd从开始运动到达最大速度的过程中ab棒受到的安培力竖直向上,且mg>BIL,故ab棒处于静止状态。设cd从开始运动到达最大速度的过程中经过的时间为t,通过的距离为x,cd棒中平均感应电动势为E1,平均电流为I1,通过cd棒横截面的电荷量为q,
由能量守恒定律得:mgxsinθ=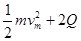 (2分)
(2分)
电动势: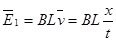 ,电流:
,电流: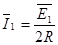 ,
,
电荷量: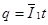 (2分)
(2分)
代入数据解得:q=1C (1分)
(3)设cd棒开始运动时穿过回路的磁通量为Φ0,cd棒在倾斜轨道上下滑的过程中,设加速度大小为a,经过时间t通过的距离为x1,穿过回路的磁通量为Φ,cd棒在倾斜轨道上下滑时间为t0,
则:Φ0=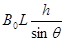 (1分)
(1分)
由牛顿第二定律mgsinθ=ma,则加速度:a=gsinθ,位移:x1=1/2(at2) (2分)
Φ=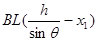 ,
,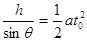 (2分)
(2分)
解得:t0=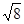 s,
s,
为使cd棒中无感应电流,必须有:Φ0=Φ,(2分)
解得: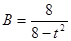 , (t<
, (t<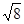 s);(2分)
s);(2分)
考点:能量守恒定律 法拉第电磁感应定律 牛顿第二定律
本题难度:困难
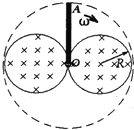
5、选择题 有一种信号发生器的工作原理可以简化为如图所示的图形,竖直面内有半径为R且相切与O点的两圆形区域,其内存在水平恒定的匀强磁场,长为2R的导体杆OA,以角速度ω绕过O点的固定轴,在竖直平面内顺时针竖直旋转,t=0时,OA恰好位于两圆的公切线上,下列描述导体杆两端电势能差UAO随时间变化的图象可能正确的是( )
A.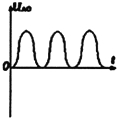
B.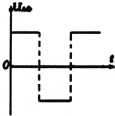
C.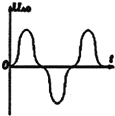
D.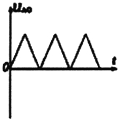
参考答案:由右手定则可判,感应电动势始终从O指向A,为正.
由E=12BL2ω,L是有效切割长度,可知,B、ω不变,切割的有效长度随时间先增大后减小,且做非线性、非正弦的变化,经半圈后,再次重复,故A正确;
故选:A.
本题解析:
本题难度:简单