时间:2019-06-26 04:11:38
1、简答题 如图(a)所示,在垂直于匀强磁场B的平面内,半径为r的金属圆盘绕过圆心O的轴转动,圆心O和边缘K通过电刷与一个电路连接,电路中的P是加上一定正向电压才能导通的电子元件.流过电流表的电流I与圆盘角速度ω的关系如图(b)所示,期中ab段和bc段均为直线,且ab段过坐标原点.ω>0代表圆盘逆时针转动.已知:R=3.0Ω,B=1.0T,r=0.2m.忽略圆盘、电流表和导线的电阻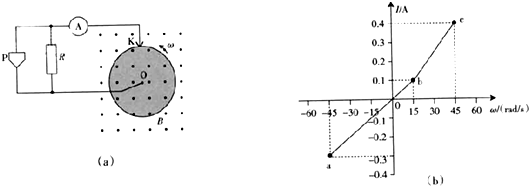
(1)根据图(b)写出ab、bc段对应I与ω的关系式
(2)求出图(b)中b、c两点对应的P两端的电压Ub、Uc
(3)分别求出ab、bc段流过P的电流Ip与其两端电压Up的关系式.
参考答案:(1)由图可知,在ab段,直线斜率k1=△I1△ω1=1150
故对应I与ω的关系式为:I=1150ω?(-45rad/s≤ω≤15?rad/s)
在bc段,直线斜率k2=△I2△ω2=1100
设表达式I=k2ω+b,把ω=45rad/s,I=0.4A代入解得b=-0.05
故对应I与ω的关系式为:I=1100ω-0.05?(15rad/s≤ω≤45?rad/s)
(2)圆盘转动时产生的感应电动势E=Brv=Br0+ωr2=12Br2ω
故b点对应的P两端的电压Ub=Eb=12Br2ωb
c两点对应的P两端的电压Uc=Ec=12Br2ωc
代入数据解得Ub=0.30V
Uc=0.90V
(3)由Up=(?I-Ip)R可知
ab段流过P的电流Ip与其两端电压Up的关系式为
Up=-3Ip+150ω?(0≤ω≤15?rad/s)
或Up=3Ip-150ω?(-45rad/s≤ω≤0)
bc段流过P的电流Ip与其两端电压Up的关系式
Up=-3Ip+3100ω-0.15?(15rad/s≤ω≤45?rad/s)
答:(1)ab、bc段对应I与ω的关系式分别为I=1150ω (-45rad/s≤ω≤15 rad/s),I=1100ω-0.05 (15rad/s≤ω≤45 rad/s).
(2)中b、c两点对应的P两端的电压分别为0.30V,0.90V.
(3)ab流过P的电流Ip与其两端电压Up的关系式分别为:Up=-3Ip+150ω (0≤ω≤15 rad/s)或Up=3Ip-150ω (-45rad/s≤ω≤0),bc段流过P的电流Ip与其两端电压Up的关系式Up=-3Ip+3100ω-0.15 (15rad/s≤ω≤45 rad/s).
本题解析:
本题难度:一般
2、选择题 某空间出现了如图所示的一组闭合的电场线,这可能是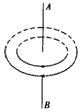
[? ]
A.沿AB方向磁场在迅速减弱
B.沿AB方向磁场在迅速增强
C.沿BA方向磁场在迅速增强
D.沿BA方向磁场在迅速减弱
参考答案:AC
本题解析:
本题难度:简单
3、选择题 如图所示装置中,cd杆原来静止.当ab杆做如下那些运动时,cd杆将向右移动( )
A.向右匀速运动
B.向右加速运动
C.向左加速运动
D.向右减速运动
参考答案:A、ab杆向右匀速运动,在ab杆中产生恒定的电流,该电流在线圈L1中产生恒定的磁场,在L2中不产生感应电流,cd不受安培力作用,所以cd杆不动.故A错误.
B、ab杆向右加速运动,根据右手定则,知在ab杆上产生增大的a到b的电流,根据安培定则,在L1中产生向上增强的磁场,该磁场向下通过L2,根据楞次定律,在cd杆上产生c到d的电流,根据左手定则,受到向右的安培力,向右运动.故B正确.
C、ab杆向左加速运动,根据右手定则,知在ab杆上产生增大的b到a的电流,根据安培定则,在L1中产生向下增强的磁场,该磁场向上通过L2,根据楞次定律,在cd杆上产生d到c的电流,根据左手定则,受到向左的安培力,向左运动.故C错误.
D、ab杆向右减速运动,根据右手定则,知在ab杆上产生减小的a到b的电流,根据安培定则,在L1中产生向上减弱的磁场,该磁场向下通过L2,根据楞次定律,在cd杆上产生d到c的电流,根据左手定则,受到向左的安培力,向左运动.故D错误.
故选:B.
本题解析:
本题难度:一般
4、选择题 如图所示,闭合金属线圈abcd位于水平方向匀强磁场的上方h处,由静止开始下落,并进入磁场,在运动过程中,线框平面始终和磁场方向垂直,不计空气阻力,那么线框在进入磁场的过程中出现( ) 
A.可能加速运动
B.一定减速运动
C.可能匀速运动
D.可能静止状态
参考答案:AC
本题解析:略
本题难度:一般
5、选择题 如图所示,垂直纸面向里的匀强磁场的区域宽度为2a,磁感应强度的大小为B。一边长为a、电阻为4R的正方形均匀导线框ABCD从图示位置沿水平向右方向以速度v匀速穿过磁场区域,在下图中线框A、B两端电压UAB与线框移动距离x的关系图象正确的是( ? )

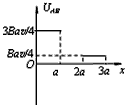
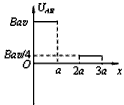
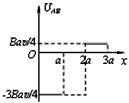
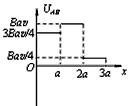
参考答案:D
本题解析:
本题难度:一般