时间:2019-06-26 04:09:14
1、选择题 一重为G的物体在重力和恒力F的共同作用下沿与竖直方向成θ角的直线匀加速向下运动,关于F的大小,下列说正确的是( )
A.一定等于Gtanθ
B.一定等于Gsinθ
C.不可能大于G
D.不可能小于Gsinθ
参考答案: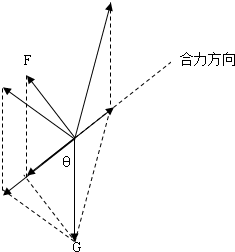
据题,物体在重力和恒力F的共同作用下沿与竖直方向成θ角的直线匀加速向下运动,根据物体做直线运动的条件可知,物体所受的合力方向必沿此直线方向,由根据平行四边定则作出力的合成图如图,由图看出,当F与此直线垂直时,F有最小值,最小值为Fmin=Gsinθ,所以F不可能小于Gsinθ,不一定等于Gtanθ,也不一定等于Gsinθ,可能大于G.所以选项ABC错误,D正确.
故选D
本题解析:
本题难度:简单
2、选择题 如图所示,足够长的传送带与水平面夹角为θ,以速度v0逆时针匀速转动。在传送带的上端轻轻放置一个质量为m的小木块,小木块与传送带间的动摩擦因数μ <tanθ,则下图中能客观地反映小木块的速度随时间变化关系的是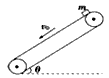
[? ]
A.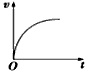
B.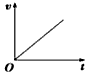
C.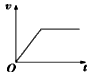
D.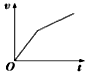
参考答案:D
本题解析:
本题难度:一般
3、计算题 如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环。棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(k>1)。断开轻绳,棒和环自由下落。假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失。棒在整个运动过程中始终保持竖直,空气阻力不计。求:
(1)棒第一次与地面碰撞弹起上升过程中,环的加速度;
(2)从断开轻绳到棒与地面第二次碰撞的瞬间,棒运动的路程S;
(3)从断开轻绳到棒和环都静止,摩擦力对环及棒做的总功W。 
参考答案:解:(1)设棒第一次上升过程中,环的加速度为a环,由牛顿第二定律得:
kmg-mg=ma环
解得:a环=(k-1)g,方向竖直向上
(2)设棒第一次落地的速度大小为v1
由机械能守恒得: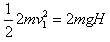
解得: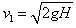
设棒弹起后的加速度为a棒,由牛顿第二定律得:
A棒=-(k+1)g
棒第一次弹起的最大高度为: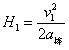
解得: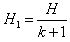
棒运动的路程为: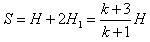
(3)解法一: 棒第一次弹起经过t1时间,与环达到相同速度v"1
环的速度:v"1=-v1+a环t1
棒的速度:v"1=v1+a棒t1
环的位移: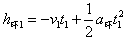
棒的位移: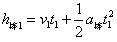
环第一次相对棒的位移为: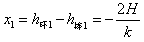
棒环一起下落至地: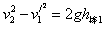
解得: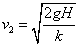
同理,环第二次相对棒的位移为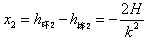
…… 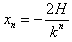
环相对棒的总位移为:x=x1+x2+……+xn
摩擦力对棒及环做的总功为: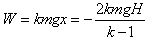
解法二: 设环相对棒滑动距离为l
根据能量守恒: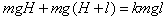
摩擦力对棒及环做的总功为: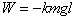
解得: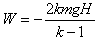
本题解析:
本题难度:困难
4、简答题 如图所示,在xOy平面内,一质量为m、电荷量为+q的粒子(重力不计)以速度v0从坐标原点O沿与+x方向成θ角射入第一象限区,并从x轴上x1=a的A点离开第一象限区,速度方向与+x方向也成θ角.
(1)若在xOy平面存在一电场,带点粒子在电场力作用下沿圆弧匀速率从O点运动到A点,θ=30°,求O点电场强度的大小E和粒子从O点运动到A点的时间t.
(2)若只存在一垂直于xOy平面的圆形匀强磁场区,磁场的磁感应强度B是可以调节的,且满足0≤B≤Bm,θ=30°,求圆形磁场区的最小半径r0.
(3)若只有第一象限内存在一垂直于xOy平面的圆形匀强磁场区,且θ=45°,求磁场的磁感应强度的最小值B0.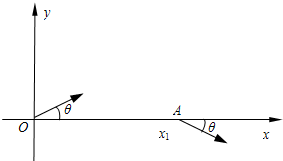
参考答案:(1)有几何关系可知,带电粒子运动的半径r1=x1=a,
粒子在电场中偏转2θ=π3,
由牛顿第二定律和运动学公式有,
qE=mv20r1
t=2θrv0
解得 E=mv20aq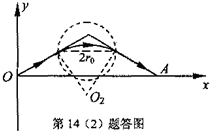
t=πa3v0
(2)如图所示,设圆周运动的最小半径为r2,则
qv0Bm=mv20r2
r0=r22
解得 r0=mv02qBm
(3)如图所示,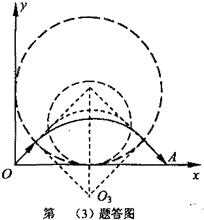
圆形磁场区只限于第一象限内,磁场磁感应强度越小,粒子回旋半径越大,则磁场区半径越大.
当磁场区圆边界与xy轴相切,磁场磁感应强度最小,
设对应的运动半径为r3,则
r3=a2
qv0B0=mv20r3
解得 B0=2mv0aq
本题解析:
本题难度:一般
5、选择题 质量为m的一物体放在升降机的水平地板上,当升降机以
| 1 3 |
| 4 3 |
| 2 3 |
| 1 3 |
参考答案:根据牛顿第二定律mg-N=ma,a=13g,得N=23mg.支持力等于物体对升降机的水平地板的压力.故C正确,A、B、D错误.
故选C.
本题解析:
本题难度:简单