时间:2019-06-23 22:54:34
1、计算题 如图,直角坐标系在一真空区域里,y轴的左方有一匀强电场,场强方向跟y轴负方向成θ=30°角,y轴右方有一垂直于坐标系平面的匀强磁场,在x轴上的A点有一质子发射器,它向x轴的正方向发射速度大小为v=2.0×106m/s的质子,质子经磁场在y轴的P点射出磁场,射出方向恰垂直于电场的方向,质子在电场中经过一段时间,运动到x轴的Q点。已知A点与原点O的距离为10cm,Q点与原点O的距离为(20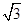 -10)cm,质子的比荷为
-10)cm,质子的比荷为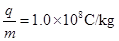 。求:
。求: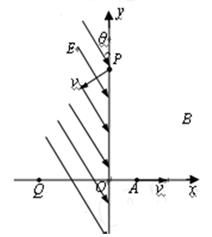
(1)磁感应强度的大小和方向;
(2)质子在磁场中运动的时间;
(3)电场强度的大小。
2、计算题 (12分)如图所示,两根平行金属导轨固定在同一水平面内,间距为l,导轨左端连接一个电阻R.一根质量为m、电阻为r的金属杆ab垂直放置在导轨上.在杆的右方距杆为d处有一个匀强磁场,磁场方向垂直于轨道平面向下,磁感应强度为B.对杆施加一个大小为F、方向平行于导轨的恒力,使杆从静止开始运动,已知杆到达磁场区域时速度为v,之后进入磁场恰好做匀速运动.不计导轨的电阻,假定导轨与杆之间存在恒定的阻力.求:
(1)导轨对杆ab的阻力大小Ff;
(2)杆ab中通过的电流及其方向;
(3)导轨左端所接电阻R的阻值.
3、简答题 如图所示,两块水平放置、相距为d的长金属板接在电压可调的电源上.两板之间的右侧区域存在方向垂直纸面向里的匀强磁场.将喷墨打印机的喷口靠近上板下表面,从喷口连续喷出质量均为m、水平速度均为v0、带相等电荷量的墨滴.调节电源电压至U,墨滴在电场区域恰能沿水平向右做匀速直线运动;进入电场、磁场共存区域后,最终垂直打在下板的M点.
(1)判读墨滴所带电荷的种类,并求其电荷量;
(2)求磁感应强度B的值;
(3)现保持喷口方向不变,使其竖直下移到两板中间的位置.为了使墨滴仍能到达下板M点,应将磁感应强度调至B’,则B’的大小为多少?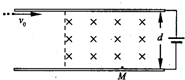
4、简答题 如图所示,一束具有各种速率的两种质量数不同的一价铜离子,水平地经过小?孔S1射入垂直的匀强电场和匀强磁场区域,已知匀强电场的场强E="1X" l05v/m,匀强磁场的磁感应强度为Bl=0.4T.求:
(1)速度多大的一价铜离子,才能通过与Sl小孔正对的S2小孔射入另一匀强磁场B2中?
(2)如果这些一价铜离子在匀强磁场B2中发生偏转后,打在过小孔S2且与两磁场分界面重合的照相底片上,已知分界面与小孔SlS2连线垂直,若感光点到小孔S2的距离分别为d1=0.654m,d2="0.674m" ,那么对应的两种铜离子的质量数之比为多大? 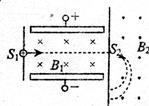
5、填空题 如图所示,是等离子体发电机的示意图,磁感应强度为B,两板间距离为d,要使输出电压为U,则等离子的速度V为_______,a是电源的_____极。