时间:2019-05-21 05:17:16
1、选择题 将一个8N的力分解为两个力，下列各组值不可能的是
A.7N，11N
B.1N，10N
C.10N，15N
D.20N，20N
参考答案：B
本题解析：分析：两个力的合力范围是大于等于两个力之差的绝对值，小于等于两个力之和，根据该规律判断选项的正确与否．
解答：A、7N与11N的合力范围是4N≤F≤18N．可能为8N．故A正确．
B、1N与10N的合力范围是9N≤F≤11N．不可能为8N．故B错误．
C、10N与15N的合力范围是5N≤F≤25N．可能为8N．故 C正确．
D、20N与20N的合力范围是0N≤F≤40N．可能为8N．故D正确．
本题选不可能的，故选B．
点评：解决本题的关键的掌握两个力的合力范围，知道合力与分力的关系．
本题难度：困难
2、选择题 F1、F2是力F的两个分力．若F=10N，则下列哪组力不可能是F的两个分力
A.F1=10N?F2=10N
B.F1=20N?F2=20N
C.F1=2?N?F2=6N
D.F1=20N?F2=30N
参考答案：C
本题解析：分析：根据合力F和两分力F1、F2之间的关系|F1-F2|≤F≤|F1+F2|，求出两个力的合力范围，判断哪一组合力不可能为10N．
解答：A、根据|F1-F2|≤F≤|F1+F2|，10N和10N的合力范围为[0N，20N]，可能为10N．故A正确．
B、根据|F1-F2|≤F≤|F1+F2|，20N和20N的合力范围为[0N，40N]，可能为10N．故B正确．
C、根据|F1-F2|≤F≤|F1+F2|，2N和6N的合力范围为[4N，8N]，不可能为10N．故C错误．
D、根据|F1-F2|≤F≤|F1+F2|，20N30N的合力范围为[10N，50N]，可能为10N．故D正确．
本题选不可能的，故选C．
点评：本题考查合力和分力之间的关系．合力F和两分力F1、F2之间的关系为|F1-F2|≤F≤|F1+F2|．
本题难度：困难
3、选择题 如图所示，质量m=5kg的物体置于一粗糙的斜面上，用一平行于斜面上的力F=30N推物体m，物体恰沿斜面向上做匀速运动，斜面体质量M=10kg，放在粗糙的水平地面上且始终静止，则下则说法正确的是
A.地面对斜面体的摩擦力向左，大小为15N
B.地面对斜面体的支持力大小为150?N
C.斜面体对物块的摩擦力大小为5?N
D.斜面对物块的作用力大小为10
参考答案：C
本题解析：分析：以滑块为研究对象，分析受力情况．滑块向上匀速运动时，合力为零，根据平衡条件求解斜面对滑块的摩擦力．
再以整体为研究对象，整体的合力为零，分析受力情况，由平衡条件求解地面对斜面体的摩擦力和支持力．
解答：以滑块为研究对象，分析受力情况如图，滑块向上匀速运动时，则有
：
F=m1gsin30°+f1，
则得斜面对滑块的摩擦力：
f1=F-m1gsin30°=30-50×0.5（N）=5N
以整体为研究对象，整体的合力为零，分析受力情况，根据平衡条件得：
水平方向：f2=Fcos30°
竖直方向：N+Fsin30°=（m1+m2）g
解得：f2=15
N，N=135N
所以C正确，AB错误；
斜面 对物块的作用力包括支持力和摩擦力，这两个力的合力应该与物块的重力相等，即大小为50N．所以D错．
故选：C．
点评：本题是两个物体平衡的问题，首先要灵活选择研究对象，其次要正确分析受力情况．本题解答采用整体法和隔离法相结合的方法，比较简便．
本题难度：简单
4、选择题 
如图，质量都是m的物体A、B用轻质弹簧相连，静置于水平地面上，此时弹簧压缩了△l．如果再给A一个竖直向下的力，使弹簧再压缩△l，形变始终在弹性限度内，稳定后，突然撤去竖直向下的力，在A物体向上运动的过程中，下列说法中：①B物体受到的弹簧的弹力是mg时，A物体的速度最大；②B物体受到的弹簧的弹力是mg时，A物体的加速度最大；③A物体受到的弹簧的弹力是mg时，A物体的速度最大；④A物体受到的弹簧的弹力是mg时，A物体的加速度最大．其中正确的是
A.只有①③正确
B.只有①④正确
C.只有②③正确
D.只有②④正确
参考答案：A
本题解析：分析：对A进行受力分析，A受弹力和重力作用，弹力大小与形变量大小成正比，物体向上先加速后减速运动，抓住加速度为0时速度最大，分析讨论选项即可．
解答：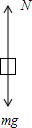
解：根据题意知mg=k△l，对A物体进行受力分析有：
释放时弹力最大，大小为2mg，随着物体上升，弹簧形变量减小弹力减小，所以：
①对A而言，因为释放时弹力大于重力，故物体向上做加速运动，当重力和弹力大小相等时，物体加速度为0，弹力再减小时合力将沿重力方向，A物体将做减速运动，故弹力为mg时，A物体的速度最大，因为弹簧对A和对B的弹力大小相等方向相反，故①正确；
②B所受弹力等于mg时，A物体所受弹力大小亦为mg，A物体所受合力为0加速度为0，故加速度最小，故②错误；
③由①分析知，③正确；
④当A物体受弹力为mg时，A所受合力为0，加速度最小，故④错误．
因为①③正确
故选A．
点评：根据胡定律知道弹簧弹力大小与弹簧的形变量成正比，轻质弹簧对连接体的弹力大小相等方向相反．
本题难度：困难
5、选择题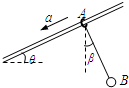 
如图所示，一固定杆与水平方向夹角θ，将一质量m1的小环A套在杆上，将质量为m2的小球B通过轻绳悬挂在环下，然后由静止释放，环沿杆下滑，稳定后悬绳与竖直方向成β角（β不为零）且保持不变，则对于系统稳定后，下列说法中正确的是
A.环与小球可能一起做匀速运动
B.若θ=β，则环与小球加速度α=gsinθ
C.若m1不变，则m2越大，β越小
D.由题给条件可判断，一定有0＜β≤θ
参考答案：BD
本题解析：分析：对小球受力分析，竖直向下的重力和沿绳子向上的拉力，所以B一定不是平衡状态，稳定后悬绳与竖直方向成β角（β不为零）且保持不变，说明小球的合外力沿杆子向下的方向，对整体受力分析后可求出加速度a，所以小球的加速度也是a，然后对重力和拉力进行合成后可小球的加速度a，利用加速度相等建立关系讨论．
解答：A：对小球受力分析，竖直向下的重力和沿绳子向上的拉力，所以B一定不是平衡状态，故A错误．
对整体受力分析如图：（当杆光滑时）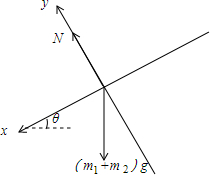
所以：合力为：（m1+m2）gsinθ，由牛顿第二定律得：
a=gsinθ
对小球受力分析如图：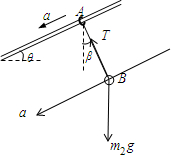
对小球由牛顿第二定律得：
m2gsinθ-Tsin（θ-β）=m2a
解得：θ=β，选项B正确．
若杆不光滑，对整体受力分析如图：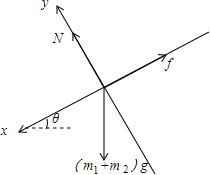
所以：y方向：N=（m1+m2）gcosθ
合力为：（m1+m2）gsinθ-f=（m1+m2）gsinθ-μ（m1+m2）gcosθ，由牛顿第二定律得：
a=gsinθ-μgcosθ＜gsinθ
对小球受力分析如图：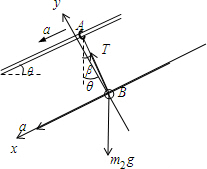
因为小球的加速度也要小于gsinθ，所以β＜θ，但一定要在竖直方向右边，所以β＞0
故：有摩擦力时，0＜β＜θ
综上所述：无摩擦时：β=θ；有摩擦时：0＜β＜θ
所以有：0＜β≤θ，故D正确．
故选：BD
点评：本题其实是牛顿运动定律的应用，连接体问题，思路就是先整体后隔离，难度不小．
本题难度：简单