2、选择题 如图所示,两个半径不同而内壁光滑的半圆轨道固定于地面,一个小球先后从与球心在同一水平高度的A、B两点由静止开始自由下滑,通过轨道最低点时(? )
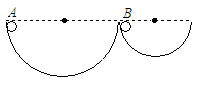
A.小球对轨道的压力相同
B.小球对两轨道的压力不同
C.此时小球的速度相等
D.此时小球的向心加速度相等
3、选择题 在一次汽车拉力赛中,汽车要经过某半径为R的圆弧形水平轨道,地面对汽车的最大静摩擦力为车重的0.1倍,汽车要想通过该弯道时不发生侧滑,那么汽车的行驶速度不应大于(?)
A.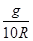
B.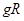
C.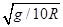
D.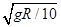
4、简答题 小球b静止在高度为H=1m的光滑平台上A处,另一小球a以水平向右的初速度v0=6m/s与小球b发生无动能损失的正碰,设a、b碰撞时间极短.小球a、b的质量分别为ma=1kg和mb=2kg.小球b碰后沿着一段粗糙的曲面进入一半径为R=0.4m的光滑竖直圆轨道中恰能通过最高点C.(g=10m/s2)求:
(1)小球b通过圆轨道最低点B时对轨道的压力大小.
(2)小球b在粗糙曲面上运动过程中克服摩擦力做的功.
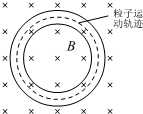
5、选择题 为了科学研究的需要,常常将带电粒子储存在圆环形状空腔中,圆环状空腔置于一个与圆环平面垂直的匀强磁场中,如图所示.如果磁场的磁感应强度为B,质子( H)和α粒子(He)在空腔中做圆周运动的轨迹相同,质子和α粒子在圆环空腔中运动的速率分别为vH和vα,运动周期分别为TH和Tα,则以下判断正确的是( )
A.vH≠vα;TH≠Tα
B.vH=vα;TH=Tα
C.vH=vα;TH≠Tα
D.vH≠vα;TH=Tα
|