时间:2018-10-13 00:47:14
1、计算题 （18分）如图所示装置的左半部分为速度选择器，相距为d的两块平行金属板分别连在电压可调的电源两极上（上板接正极），板间存在方向垂直纸面向里、磁感应强度为B0的匀强磁场；右半部分为一半径为R的半圆形磁场区域，内有垂直纸面向外、磁感应强度为B的匀强磁场．矩形abcd相切于半圆，小孔M、N连线延长线经过圆心O点且与ad垂直．一束质量为m、带电量为+q的离子（不计重力）以不同速率沿MN方向从M孔射入．
（1）金属板间电压为U0时，求从N孔射出的离子的速度大小；
（2）要使离子能打到ab上，求金属板间电压U的取值范围．
参考答案：（1）
（2）
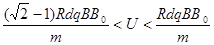
本题解析：（1）设电压为U0时，两板间电场强度为E，从N孔射出的粒子速度为v，则
①， 由平衡条件得
②
解得： ③
（2）如答图(
本题难度：一般
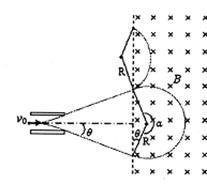
2、简答题 如图所示，真空中两平行金属板A、B长L1=0.10m，间距d=
/30m，两极板接在电压UAB=200sinl00πt（V）的交流电源上，与AB板相距L2=0.20m的PS右侧区间有一个范围足够大的匀强磁场，磁场方向垂直纸面向里，磁感应强度为B=×l0-2T。一束带正电的粒子以Vo=×105m/s的速度沿着A,B两极板的中央飞入电场，粒子的比荷q/m=1×l08C/kg，不计粒子的重力和粒子间的相互作用力，不考虑相对论效应。问：
（1）通过计算说明，带电粒子经过平行金属板期间，加在两板间的电压几乎不变；
（2）在t=0时刻进入电场的粒子，飞离磁场时离O点的距离；
（3）何时进入电场的粒子,从进入电场到离开磁场所经历的时间最长?并计算最长时间。
参考答案：
(1) 因t0≤T，所以每个粒子飞越金属板的过程中，可以认为两板问电压不变。
(2) 0.2m
(3) 
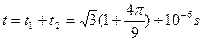
本题解析：（1）粒子飞越电场的时间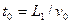
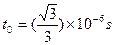（2分）
T="0.02s?" （1分）
因t0≤T，所以每个粒子飞越金属板的过程中，可以认为
两板问电压不变。?（2分）
（2）当t=0时，uAB=0粒子傲匀速直线运动，从O点进入磁场?
洛仑兹力提供向心力，有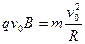
?（2分）
本题难度：一般
3、选择题 如图所示装置处于真空中，S为能放出α、β和γ三种射线的放射源，虚线框内是方向垂直纸面的匀强磁场，L是1mm厚的纸板，M是荧光屏，实验时发现在荧光屏上O、P处有亮斑．则以下判断正确的是（ ）
A．如果磁场方向垂直纸面向里，则O点和P点分别为β和α射线形成的亮斑
B．如果磁场方向垂直纸面向外，则O点和P点分别为γ和β射线形成的亮斑
C．如果磁场方向垂直纸面向里，则O点和P点分别为α和β射线形成的亮斑
D．如果磁场方向垂直纸面向外，则O点和P点分别为γ和α射线形成的亮斑
参考答案：因为α粒子的贯穿本领较小，一张纸即可把它挡住，所以亮斑中不可能有α射线，AD错误；
因为γ射线不带电，所以不受磁场约束，直接打在O点，B正确C错误．
故选B
本题解析：
本题难度：简单
4、选择题 如图所示，一束质量、速率、带电量均未知的正离子射入如图所示的电场与磁场正交的区域I，发现有些离子毫无偏移地通过这一区域，随后立即又垂直进入II的匀强磁场区域，但却分成了几束，对这些离子来说，它们可能具有（ ）
A．相同的速率，不相同的质量，相同的电量
B．相同的速率和质量，不同的电量
C．速率、质量和电量都相同
D．速率、质量和电量都不相同
参考答案：
正离子在有正交的电场和磁场的区域Ⅰ中做直线运动，对其受力分析，受向下的电场力和向上的洛伦兹力作用，有：
qE=qvB，可得：
v=EB
说明这些粒子具有相同的速率．可排除选项D．
在区域Ⅱ中这些正离子的半径并不相同，由半径公式r=mvqB=mq×EB2，可知比荷一定不相同．从而可排除选项C．
因比荷一定不同，所以质量和电量可以不同．选项AB正确．
故选AB．
本题解析：
本题难度：一般
5、简答题 如图所示，在xoy平面内y轴与MN边界之间有沿x轴负方向的匀强电场，y轴左侧和MN边界右侧的空间有垂直纸面向里、磁感应强度大小相等的匀强磁场，MN边界与y轴平行且间距保持不变．一质量为m、电荷量为-q的粒子以速度v0从坐标原点O沿x轴负方向射入磁场，每次经过磁场的时间均为t0，粒子重力不计．
（1）求磁感应强度的大小B．
（2）若t=5t0时粒子回到原点O，求电场区域的宽度d和此时的电场强度E0．
（3）若带电粒子能够回到原点0，则电场强度E应满足什么条件？
参考答案：粒子在磁场中运动的周期为：T=2πmqB…①
粒子每次经过磁场时间为半个周期：t0=T2…②
由①②解得：B=πmqt0
（2）粒子t=5t0回到原点，轨迹如图，由几何关系知r1=r2
根据：qv0B=mv20r1
qBv2=mv22r2
电场宽度：d=v0+v22t0
解得：d=3v02t0
又v2=v0+qE0mt0
解得：E0=mv0qt0
（3）如图所示，由几何关系知，要使粒子经过原点，应满足
n（2r′2-2r1）=2r1，n=1，2，3，…
由：qBv′2=mv′22r′2
解得：v′2=n+1nv0
根据动能定理知：
Eqd=12mv′22-12mv20
解得：E=(2n+1)mv03n2qt0（n=1，2，3，…）
答：（1）求磁感应强度的大小为πmqt0；
（2）若t=5t0时粒子回到原点O，电场区域的宽度d=3v02t0，此时的电场强度E0=mv0qt0；
（3）若带电粒子能够回到原点0，则电场强度为(2n+1)mv03n2qt0（n=1，2，3，…）．
本题解析：
本题难度：一般