时间:2018-10-11 00:30:00
1、计算题 一根长为L的轻杆，一端固定一质量为m的小球A，另一端固定在水平转动轴上.现使小球绕杆的另一端的转轴在竖直平面内做圆周运动，如图.试求：
（1）假设小球转至最低点时，小球的速度大小为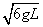
，求此时杆对小球的作用力的大小；
（2）假设小球转至最高点时，小球的速度大小为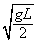
，此时杆对小球的作用力是支持力还是拉力？此力为多大？
参考答案：（1）7mg；
（2）支持力，mg/2
本题解析：
本题难度：一般
2、简答题 如图所示，圆锥摆的摆长l=50cm，摆角a=37°．试求：
（1）小球的线速度υ；
（2）如小球在运动中，细绳突然断开，小球将落向地面，已知悬点O离地面的高为1.2m，则小球落地点到悬点O的水平距离多大？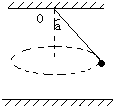
参考答案：（1）小球做匀速圆周运动，合力指向圆心，对小球受力分析，受重力和拉力，如图所示；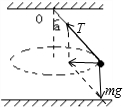
根据平行四边形定则，有：F合=mgtan37°；
解得：F合=0.75mg；
合力提供向心力，故：
F合=mv2R；
解得：v=
本题解析：
本题难度：简单
3、选择题 如图所示的圆锥摆中，摆球A在水平面上作匀速圆周运动，关于A的受力情况，下列说法中正确的是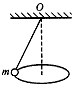
[? ]
A．摆球A受重力、拉力和向心力的作用
B．摆球A受拉力和向心力的作用
C．摆球A受拉力和重力的作用
D．摆球A受重力和向心力的作用
参考答案：C
本题解析：
本题难度：简单
4、简答题 质量相等的两汽车以相同的速度v分别通过半径为R的凸形路面P与凹形路面P′时两路面所受的压力之比为FP：FP′=______．
参考答案：汽车过凸形路面的最高点时，设速度为V，半径为R，由牛顿第二定律得：mg-FP=mv2R，
∴FP=mg-mv2R，
汽车过凹形路面的最高低时，设速度为V，半径为R，由牛顿第二定律得：FP′-mg=mv2R，
∴FP′=mg+mv2R，
所以凸形路面P与凹形路面P′时两路面所受的压力之比为gR-v2gR+v2
故答案为：gR-v2gR+v2
本题解析：
本题难度：一般
5、简答题 如图，把质量为0.6kg的物体A放在水平转盘上，A的重心到转盘中心O点的距离为0.2m，若A与转盘间最大静摩擦力为3N，g=10m/s2，求：
（1）转盘绕中心O以ω=2rad/s的角速度旋转，A相对转盘静止时，转盘对A摩擦力的大小与方向；
（2）为使物体A相对转盘静止，转盘绕中心O旋转的角速度ω的取值范围．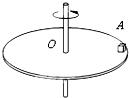
参考答案：（1）静摩擦力提供向心力，有：f=mrω2=0.6×0.2×4N=0.48N．
故转盘绕中心O以ω=2rad/s的角速度旋转时，A受到的摩擦力大小为0.48N，方向指向圆心．
（2）当A所受最大静摩擦力提供向心力时，转盘绕中心O旋转的角速度ω最大，
由fm=mωmax2r
解得：ωmax=
本题解析：
本题难度：一般