时间:2018-10-02 04:09:09
1、计算题 如图所示，在平面坐标系xOy内，第Ⅱ、Ⅲ象限内存在沿y轴正方向的匀强电场，第I、Ⅳ象限内存在半径为L的圆形匀强磁场，磁场圆心在M（L，0）点，磁场方向垂直于坐标平面向外。一带正电粒子从第Ⅲ象限中的Q（- 2L，-L）点以速度v。沿x轴正方向射出，恰好从坐标原点0进入磁场，从P（2L，0）点射出磁场。不计粒子重力，求：
（1）电场强度与磁感应强度大小之比；
（2）粒子在磁场与电场中运动时间之比。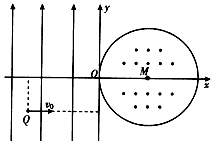 
参考答案：解：（1）设粒子的质量和所带电量分别为m和q，粒子在电场中运动，如图所示。
由平抛运动规律及牛顿运动定律得2L=v0tl ，
，qE=ma
粒子到达O点时沿+y 方向分速度为vy =atl=v0 
粒子在磁场中的速度为
由
由几何关系得
得
。
（2）粒子在磁场中运动的周期
粒子在磁场中运动时间为
得
。
本题解析：
本题难度：困难
2、计算题 （16分）如图所示，有一对平行金属板，两板相距为0.05m．电压为10V；两板之间有匀强磁场，磁感应强度大小为B0=0.1T，方向与金属板面平行并垂直于纸面向里．图中右边有一半径R为0.1m、圆心为O的圆形区域内也存在匀强磁场，磁感应强度大小为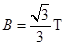
，方向垂直于纸面向里．一正离子沿平行于金属板面，从A点垂直于磁场的方向射入平行金属板之间，沿直线射出平行金属板之间的区域，并沿直径CD方向射入圆形磁场区域，最后从圆形区域边界上的F点射出．已知速度的偏向角
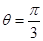，不计离子重力．求：
（1）离子速度v的大小；
（2）离子的比荷q/m；
（3）离子在圆形磁场区域中运动时间t．
参考答案：（1）
?（2）
?（3）
本题解析：（1）离子在平行金属板之间做匀速直线运动，洛仑兹力与电场力相等，即
?（2分）
?（2分）
解得?（1分）
（2）在圆形磁场区域，离子做匀速圆周运动，由洛仑兹力公式和牛顿第二定律有
?（2分）
由几何关系有
?（2分）
离子的比荷?（2分）
（3）弧CF对应圆心角为
，离子在圆形磁场区域中运动时间
，
?（2分）
又周期
?（1分）
?（2分）
本题难度：一般
3、选择题 如图所示，一对平行正对的金属板A、B，间距为d=0.1m，且极板足够长，极板间有垂直纸面向里的匀强磁场，磁感应强度B=0.1T，连接在如图所示的电路中，其中电阻R1=lΩ，R2=3Ω，电容器的电容C=20μF，电流表为理想电表．现在从图中O1点以v0=1.0×l03 m/s的速度平行于极板A、B射入一束等离子体（含有大量的正离子相负离子，且不计重力），A、B构成一个磁流体发电机，当电路稳定后，电流表示数I=2A，则（ ）
A．该磁流体发电机极板A带正电，B带负电
B．该磁流体发电机的电动势为10V
C．电容器C、电阻R2两端的电压均为10V
D．电容器带电量为1.2×10-4C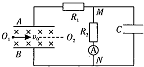
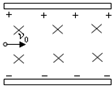
参考答案：A、等离子群射入磁场中，受到洛伦兹力，带正电荷的离子将打到电容器A极板上，负电荷达到B板，从而产生电场，故该磁流体发电机极板A带正电，B带负电，故A正确；
B、当后来的离子所受的洛伦兹力与电场力平衡时，电容器的电压和电量都稳定，由平衡条件得：qvB=qUd，得：U=Bvd=0.1×0.1×1×103V，故B正确；
C、稳定时电动势是一定的，R1、R2串联，电容器与R2并联，电压等于：U2=IR2=6V，故C错误；
D、电容器的电量为：Q=CU2=20×10-6×6=1.2×10-4C．故D正确．
故选：ABD．
本题解析：
本题难度：一般
4、选择题 如图所示，带电粒子以水平速度v0垂直进入正交的匀强电场和匀强磁场区域中，穿出电磁场区域时速度为v，电场强度为E，磁感应强度为B，则粒子的径迹、v与v0的大小关系为（ ）
A．要使粒子能沿直线运动，正电荷应从左边射入，负电荷应从右边射入
B．当v0=
| E B |
| E B |
| E B |
参考答案：A、若是正电荷，从左端进入复合场，则洛伦兹力向上，电场力向下．如电场力与洛伦兹力等大，则能沿直线通过；若是负电荷，从左端进入复合场洛伦兹力向下，电场力向上，若等大则也可以沿直线通过．故A错误．
B、如粒子沿直线通过，电场力与洛伦兹力等大反向，由有qE=Bqv0，即v0=EB．所以当v0=EB沿直线穿过，又因为在复合场中运动时洛伦兹力不做功，粒子沿电场方向无位移，故电场力也不做功，故v=v0，故B正确．
C、当v0＜EB，洛伦兹力小于电场力，正电荷粒子会向上偏，即沿电场方向上有位移．电场力对离子做正功，所以v＞v0，故C正确．
D、当v0＞EB时，洛伦兹力大于电场力，粒子将向下运动，故D错误．
故答案为：BC
本题解析：
本题难度：一般
5、计算题 （18分）如图所示，平行且足够长的两条光滑金属导轨，相距0．5 m，与水平面夹角为30°，不计电阻，广阔的匀强磁场垂直穿过导轨平面，磁感应强度B=0．4 T，垂直导轨放置两金属棒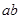
和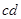
，长度均为0．5 m，电阻均为0．1Ω，质量分别为0．1 kg和0．2 kg，两金属棒与金属导轨接触良好且可沿导轨自由滑动。现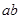棒在外力作用下，以恒定速度ν=1.5m/s沿着导轨向上滑动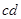，棒则由静止释放。试求：（取g="10" m／s2）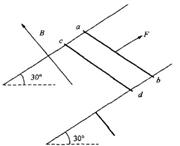
（1）金属棒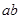产生的感应电动势；
（2）闭合回路中的最小电流和最大电流；
（3）金属棒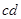的最终速度。
参考答案：（1）
（2）
?
（3）
本题解析：(18分)
（1）
---------------------------（3分）
（2）刚释放棒时，
? ---------------------------（2分）?棒受到安培力为：
-------------------（1分）棒受到的重力为：
? ---------------------------（1分）?
棒沿导轨向下加速运动，即
闭合回路的
增大；电流也将增大，所以最小电流为：? ---------------------------（4分）?
当棒的速度达到最大时，同路的电流最大，此时棒的加速度为零。
由
得：---------------------------（4分）?
（3）由
得：---------------------------（3分）
本题考查的是电磁感应定律和力学综合的问题，首先根据电磁感应定律计算出感应电动势；然后根据安培力的计算和力学规律计算出最大最小电流；最后根据欧姆定律计算出电压；
本题难度：一般