时间:2018-10-01 00:59:01
1、选择题 如图所示，通电硬直导线ab平行条形磁铁放置，导线可以在空中自由运动，其中的电流方向由a到b，则导线的运动情况为（ ）
A．a端转向纸里，b端转向纸外，且远离磁铁
B．a端转向纸里，b端转向纸外，且靠近磁铁
C．a端转向纸外，b端转向纸里，且远离磁铁
D．a端转向纸外，b端转向纸里，且靠近磁铁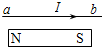
参考答案：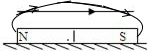
条形磁铁的磁感线如图所示，
则由图示可知左侧导体所处的磁场方向斜向上，右侧导体所处的磁场斜向下，则由左手定则可知，左侧导体受力方向向外，右侧导体受力方向向里，故从上向下看，小磁针应为逆时针转动；当导体转过90°时，由左手定则可得导体受力向下，故可得出导体运动为逆时针转动的同时还要向下运动．即为a端转向纸外，b端转向纸里，且靠近磁铁，
故选：D
本题解析：
本题难度：简单
2、计算题 有一等腰直角三角形区域，直角边长为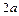
。在该区域，有一垂直纸面向内磁感应强度为
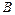的匀强磁场。一束质量为
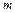、电荷量为
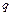，速度范围在
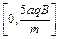之间的带负电粒子从中点
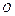垂直直角边射入该磁场区域，在另一直角边放置一块足够大的荧光屏，如图所示。重力不计，求
（1）速度至少为多大的带电粒子，能够在荧光屏上留下光斑。
（2）粒子在磁场中运动的时间和速度的关系。
（3）磁场区域内，荧光屏上亮点的位置和速度的关系。
（4）荧光屏上光斑的分布区域。
参考答案：（1）根据带电粒子在磁场中运动规律，可得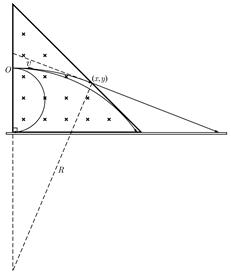
?
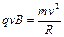求出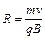
?1
在荧光屏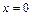
处，对应的半径为
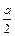，粒子速度为
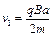?2
故小于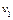
的带电粒子不能在荧光屏上留下痕迹。
（2）当半径满足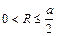
时，粒子运动时间为
?
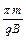当半径满足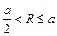
时，由图可得
，
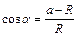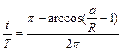
求出：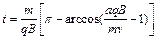
?3
当半径大于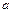
时，由图可知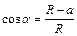
求出：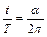
，
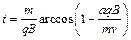?4
（3）如图，根据几何关系可知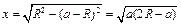
?5
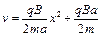?6
这是一条抛物线
（4）在磁场区域内，为了求出荧光屏最远处亮点坐标。如图可得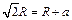
求出相切位置对应的半径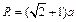
对应的最远坐标为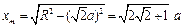
?7
对应的速度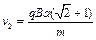
在磁场区域外，最远处的坐标可以参考图示求出。
先求出最大速度对应的半径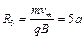
圆心坐标为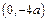
圆方程为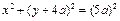
直线方程为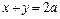
解出圆与直线的交点：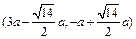
?8
过交点的切线方程为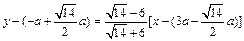
当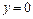
时。求出，最远处的光斑坐标为
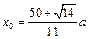?9
所以，光斑分布区域为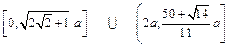
。?10
本题解析：略
本题难度：一般
3、选择题 如图所示，一块长度为a、宽度为b、厚度为d的金属导体，当加有与侧面垂直的匀强磁场B，且通以图示方向的电流I时，用电压表测得导体上、下表面MN间电压为U。已知自由电子的电量为e。下列说法中正确的是
[? ]
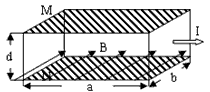
参考答案：CD
本题解析：
本题难度：一般
4、计算题 如图所示，套在很长的绝缘直棒上的小球，其质量为m，带电荷量是+q，小球可在棒上滑动，将此棒竖直放在相互垂直且沿水平方向的匀强电场和匀强磁场中，电场强度为E，磁感应强度是B，小球与棒的动摩擦因数为μ，求小球由静止沿棒下落的最大加速度和最大速度．（设小球带电荷量不变）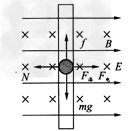
参考答案：解：小球的受力情况如题图所示
由于N=qE+qvB，所以F合=mg-μN= mg-μ(qE+qvB)
可见随着v的增大，F合减小，由牛顿第二定律可知，小球先做加速度越来越小的变加速运动，最后做匀速直线运动
故当v=0时，a最大，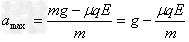
当F合=0，即a=0时v有最大值vmax，即mg-μ(qvmaxB+qE) =0，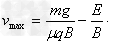
本题解析：
本题难度：一般
5、选择题 有三束粒子,分别是质子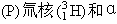
粒子束.当它们以相同的速度沿垂直磁场方向射入同一匀强磁场中，在下列四图中，能正确表示出这三束粒子运动轨迹的是[ ]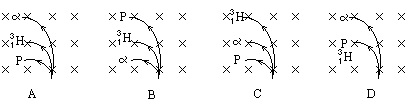
?
参考答案：C
本题解析：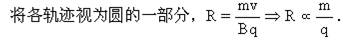
本题难度：简单