时间:2017-11-10 07:51:12
1、简答题 如图所示是说明示波器工作原理的示意图，已知两平行板间的距离为d、板长为l．电子经电压为U1的电场加速后从两平行板间的中央处垂直进入偏转电场，设电子质量为m、电量为e．求：
（1）经电场加速后电子速度v的大小；
（2）要使电子离开偏转电场时的偏转角度最大，两平行板间的电压U2应是多大？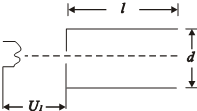
参考答案：解（1）经电场加速后电子的动能定理得
eU1=12mv2
则经电场加速后电子的速度为：v=
本题解析：
本题难度：一般
2、简答题 在半径为R的半圆形区域中有一匀强磁场，磁场的方向垂直于纸面，磁感应强度为B．一质量为m，带有电量q的粒子以一定的速度沿垂直于半圆直径AD方向经P点（AP=d）射入磁场（不计重力影响）．
（1）如果粒子恰好从A点射出磁场，求入射粒子的速度．
（2）如果粒子经纸面内Q点从磁场中射出，出射方向与半圆在Q点切线方向的夹角为φ（如图）．求入射粒子的速度．
参考答案：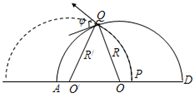
（1）由于粒子在P点垂直射入磁场，故圆弧轨道的圆心在AP上，AP是直径．
设入射粒子的速度为v1，由洛伦兹力的表达式和牛顿第二定律得：mv21d2=qBv1
解得：v1=qBd2m
（2）设O′是粒子在磁场中圆弧轨道的圆心，连接O′Q，设O′Q=R′．
由几何关系得：∠OQO′=φ? OO′=R′+R-d
由余弦定理得：(OO/)2=R2+R/2-2RR/cosφ
解得：R/=d(2R-d)2[R(1+cosφ)-d]
设入射粒子的速度为v，由mv2R/=qvB
解出：v=qBd(2R-d)2m[R(1+cosφ)-d]
答：（1）如果粒子恰好从A点射出磁场，入射粒子的速度为qBd2m．
（2）如果粒子经纸面内Q点从磁场中射出，出射方向与半圆在Q点切线方向的夹角为φ（如图）．入射粒子的速度为qBd(2R-d)2m[R(1+cosφ)-d]．
本题解析：
本题难度：一般
3、简答题 一个质量为m带电量为+q的小球每次均以水平初速度v0自h高度做平抛运动．不计空气阻力，重力加速度为g，试回答下列问题：
（1）若在空间竖直方向加一个匀强电场，发现小球水平抛出后做匀速直线运动，则电场强度E是多大？
（2）撤消匀强电场，小球水平抛出至第一落地点P，则位移S的大小是多少？
（3）恢复原有匀强电场，再在空间加一个垂直纸面向外的匀强磁场，发现小球第一落地点仍然是P点，试问磁感应强度B是多大？
参考答案：（1）小球做匀速直线运动，根据平衡条件：mg=qE，
得：E=mgq；
（2）小球做平抛运动，水平方向：x=v0t，
竖直方向：h=12gt2
得到：S=
本题解析：
本题难度：一般
4、计算题 在直径为d的圆形区域内存在均匀磁场、磁场方向垂直于圆面指向纸外。一电量为q、质量的m的粒子，从磁场区域的一条直径AC上的A点射入磁场，其速度大小为v0，方向与AC成α角。若此粒子恰好能打在磁场区域圆周上的D点，AD与AC的夹角为β，如图所示，求该匀强磁场的磁感应强度B的大小。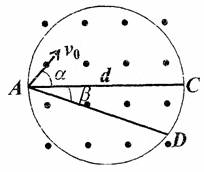
参考答案：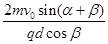
本题解析：设粒子在磁场中圆周运动半径为R，其运动轨迹如图所示，O为圆心，则有：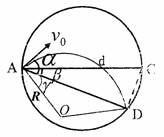
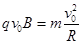?又设AO与AD的夹角为
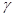，由几何关系知：
?，
?，
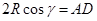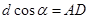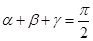可得：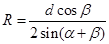
则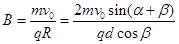
点评：对带电粒子在有界磁场中匀速圆周运动的求解，关键是画出匀速圆周运动的轨迹，利用几何知识找出圆心及相应的半径，由圆心和轨迹用几何知识确定半径是研究带电粒子在匀强磁场中做匀速圆周运动的重要方法，题目的难度在于对几何知识的应用上。
本题难度：一般
5、选择题 如图，圆形区域内有一垂直纸面的匀强磁场，P为磁场边界上的一点。有无数带有同样电荷、具有同样质量的粒子在纸面内沿各个方向以同样的速率通过P点进入磁场。这些粒子射出边界的位置均处于边界的某一段弧上，这段圆弧的弧长是圆周长的1/3。将磁感应强度的大小从原来的B1变为B2，结果相应的弧长变为原来的一半，则B2/B1等于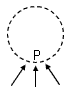 
[? ]
A．2
B．3
C．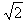
D．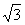
参考答案：D
本题解析：
本题难度：一般