时间:2017-11-10 07:51:12
1、选择题 如图所示，用铝板制成“?”形框，将一质量为m的带电小球用绝缘细线悬挂在框的上方，让整体在垂直于水平方向的匀强磁场中向左以速度v匀速运动，悬线拉力为T，则（ ）
A．悬线竖直，T=mg
B．悬线竖直，T＜mg
C．v选择合适的大小，可使T=0
D．因条件不足，T与mg的大小关系无法确定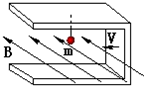
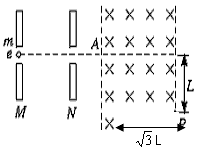
2、计算题 电子（不计重力）自静止开始经M、N板间（两板间电压为u）的电场加速后从A点垂直于磁场边界射入宽度为
L的匀强磁场中，电子离开磁场时的位置P偏离入射方向的距离为L，如图所示（已知电子的质量为m，电量为e）求：
（1）电子在加速电场中加速后获得的速度；
（2）匀强磁场的磁感应强度；
（3）电子在磁场中的运动时间。
3、计算题 如图（a）所示，为某同学设想的粒子速度选择装置，由水平转轴及两个薄盘N1、N2构成，两盘面平行且与转轴垂直，相距为L，盘上各开一狭缝，两狭缝夹角θ可调（如图（b））；右为水平放置的长为d的感光板，板的正上方有一匀强磁场，方向垂直纸面向外，磁感应强度为B一小束速度不同、带正电的粒子沿水平方向射人N1，能通过N2的粒子经O点垂直进入磁场O到感光板的距离为d/2，粒子电荷量为q，质量为m，不计重力
（1）若两狭缝平行且盘静止（如图（c）），某一粒子进入磁场后，竖直向下打在感光板中心点M上，求该粒子在磁场中运动的时间t；
（2）若两狭缝夹角为θ0，盘匀速转动，转动方向如图（b）要使穿过N1、N2的粒子均打到感光板P1P2连线上，试分析盘转动角速度ω的取值范围（设通过N1的所有粒子在盘旋转一圈的时间内都能到达N2）。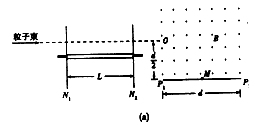 
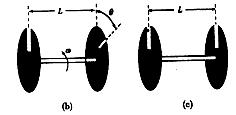
4、选择题 如图所示，以直角三角形AOC为边界的有界匀强磁场区域，磁感应强度为B，∠A=60°，AO=a。在O点放置一个粒子源，可以向各个方向发射某种带负电粒子，粒子的电量大小为q，质量为m，发射速度大小都为v0，发射方向由图中的角度θ表示．不计粒子间的相互作用及重力，下列说法正确的是（?）
A．若v0=
，则以θ=0°方向射入磁场的粒子在磁场中运动的时间为
B．若v0=
，则以θ＝60°飞入的粒子在磁场中运动时间最短
C．若v0=，则以θ<30°飞入的粒子在磁场中运动的时间都相等
D若v0=，则在AC边界上只有一半区域有粒子射出
5、计算题 如图所示的正方形平面oabc内，存在着垂直于该平面向外的匀强磁场，磁感应强度大小为B，已知正方形边长为L，一质量为m，带电量为+q的粒子（不计重力）在t=0时刻平行于oc边从o点射入磁场中。
（1）若带电粒子从a点射出磁场，求带电粒子在磁场中运动的时间以及初速度的大小；
（2）若磁场的磁感应强度按如图所示的规律变化，规定磁场向外的方向为正方向，磁感应强度的大小为B0，则要使带电粒子能从oa边界射出磁场，磁感应强度B的变化周期T的最小值应为多少？
（3）若所加磁场与第（2）问中相同，则要使粒子从b点沿ab方向射出磁场，满足这一条件的磁感应强度的变化周期T及粒子射入磁场时的速度V0应为多少？（不考虑磁场变化产生的电场）