时间:2017-11-05 16:51:04
1、选择题 关于一定质量的气体的压强、体积、温度的关系,下述现象可能发生的是
A.体积不变时,温度升高,压强增大
B.温度不变时,压强不变,体积增大
C.压强不变时,温度降低,体积增大
D.密度不变时,温度降低,压强增大
参考答案:A
本题解析:根据一定质量的理想气体状态方程: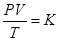 进行判断。
进行判断。
A.体积不变,温度升高,压强增大,正确;
B.温度不变,压强不变,则体积不变,该选项错误;
C.压强不变,温度降低,体积减小,故该选项错误;
D.密度不变,相当于体积不变,温度降低,压强减小,故该选项错误,
故答案选A.
本题难度:简单
2、简答题 如图所示,汽缸A和B的活塞用硬杆相连,活塞的面积s1=2s2,两活塞离底部距离均为h,汽缸壁用导热材料做成,此时环境温度为300K,外界大气压为p0,汽缸B内的压强p2=0.5p0。问:(1)此时汽缸A内气体的压强为多少?(2)若保持汽缸B中的气体温度不变,把汽缸A缓慢加热,问加热至温度多高活塞才移动 ?
?
参考答案:(1)0.75p0(2) 600K
本题解析:(1)要求汽缸内封闭气体的压强,应分析活塞总体,通过受力分析,根据共点力平衡条件求解。活塞整体受力分析如图,根据共点力平衡有:
 ,解得:p1=0.75p0
,解得:p1=0.75p0
(2)将汽缸A加热过程中,A、B两部分气体状态变化满足气体方程,终态时活塞整体仍满足共点力平衡条件。对气体A:
对气体B:
根据活塞平衡:
解得T’=600K。
本题难度:简单
3、填空题 如图所示,竖直放置的弯曲管A端开口,C端封闭,密度为ρ的液体将B、C两段空气封闭在管内,管内液面高度差分别为h1、h2和h3,已知大气压强为p0,则B段气体的压强为 ,C段气体的压强为 。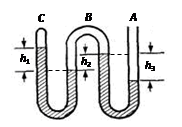
参考答案:p0-ρgh3 ,p0- ρgh3-ρgh1
本题解析:分析:根据液面的高度关系分析,大气压强P0等于B段气体产生的压强加上h3液体产生的压强,中间这段气体产生的压强等于C端气体产生的压强加上h1液体产生的压强,据此分析整理.
解答:解:由图中液面的高度关系可知,P0=PB+ρgh3 ,P0=P2+ρgh3 和 PB=PC+ρgh1,由此解得PB=P0-ρgh3 ,PC=P0-ρg(h1+h3)
故答案为:P0-ρgh3 ,P0-ρg(h1+h3)
点评:很多学生会错误认为 P0<PB 和 PB<PC,此外图中 h2 是一个干扰条件,而实际上中间气体的压强与中间两液面的高度差无关.
在计算气体压强时,有两个结论可以直接应用①同一气体的压强处处相等 ②同一液体内部不同点间的压强差由高度差决定,并且位置越高,压强越小.
本题难度:一般
4、简答题 一密封的气象探测气球,在地面时充有压强为1.0×105Pa、温度为27.0℃的氦气时,体积为4.0m3,气球内氦气的密度为1.0Kg/m3,摩尔质量为4g/mol.在上升至海拔10.0k.m高空的过程中,气球内氦气逐渐减小到此高度上的大气压4×104Pa,气球内部因启动一持续加热过程而维持其温度不变.此后停止加热,保持高度不变.已知在这一海拔高度气温为-33.0℃.已知阿伏伽德罗常数为N=6.0×1023mol-1.求:
(1)气球内氦气的分子数
(2)氦气在停止加热前的体积;
(3)氦气在停止加热较长一段时间后的体积.
参考答案:(1)氦气分子个数:n=mMN=ρV0MN=1×40.004×6.0×1023=6.0×1026个;
(2)由题意知,气体状态参量为:p1=1.0×105Pa,V1=4m3,p2=4×104Pa,
气体温度不变,由玻意耳定律得:p1V1=p2V2,代入数据解得:V2=10m3.
(3)经过较长时间后,气体温度与环境温度相等,
气体状态参量为:V2=10m3,T2=T1=273+27=300K,T3=273-33=240K,
气体压强不变,由盖吕萨克定律得:V2T1=V3T2,代入数据解得:V3=8m3.
答:(1)气球内氦气的分子数为6.0×1026个.
(2)氦气在停止加热前的体积为10m3;
(3)氦气在停止加热较长一段时间后的体积为8m3.
本题解析:
本题难度:一般
5、选择题 一定质量的理想气体,处在某一初始状态.现要使它的温度经过一系列的状态变化后,回到初始温度,下列哪些过程可以实现?( ? )
A.先等压压缩,后等容增压
B.先等压压缩,后等容降压
C.先等容增压,后等压膨胀
D.先等容降压,后等压膨胀
参考答案:AD
本题解析:
本题难度:一般