时间:2017-11-05 16:34:51
1、计算题 质量为3
参考答案:
本题解析:
本题难度:一般
2、计算题 如图所示,斜面倾角为θ,在斜面底端垂直斜面固定一挡板,轻质弹簧一端固定在挡板上,质量为M=1.0 kg的木板与轻弹簧接触但不拴接,弹簧与斜面平行且为原长,在木板右上端放一质量为m=2. 0 kg的小金属块,金属块与木板间的动摩擦因数为μ1=0.75,木板与斜面粗糙部分间的动摩擦因数为μ2=0.25,系统处于静止状态.小金属块突然获得一个大小为v1=5.3 m/s、方向平行斜面向下的速度,沿木板向下运动.当弹簧被压缩x=0.5 m到P点时,金属块与木板刚好达到相对静止,且此后运动过程中,两者一直没有发生相对运动.设金属块从开始运动到与木块达到相同速度共用时间t=0.75 s,之后木板压缩弹簧至最短,然后木板向上运动,弹簧弹开木板,弹簧始终处于弹性限度内,已知sin θ=0.28、cos θ=0.96,g取10 m/s2,结果保留二位有效数字.
(1)求木板开始运动瞬间的加速度;
(2)求弹簧被压缩到P点时的弹性势能是多少?
(3)假设木板在由P点压缩弹簧到弹回到P点过程中不受斜面摩擦力作用,木板离开弹簧后沿斜面向上滑行的距离?
参考答案:(1)10 m/s2,沿斜面向下(2)3.0 J(3)s=0.077 m
本题解析:(1)对金属块,由牛顿第二定律可知加速度大小为
a=μ1gcos θ-gsin θ=4.4 m/s2,沿斜面向上(1分)
木板受到金属块的滑动摩擦力F1=μ1mgcos θ=14.4 N,沿斜面向下(1分)
木板受到斜面的滑动摩擦力
F2=μ2(M+m)gcos θ=7.2 N,沿斜面向上(1分)
木板开始运动瞬间的加速度a0= =10 m/s2,沿斜面向下(1分)
=10 m/s2,沿斜面向下(1分)
(2)设金属块和木板达到共同速度为v2,对金属块,应用速度公式有v2=v1-at=2.0 m/s(1分)
在此过程中分析木板,设弹簧对木板做功为W,其余力做功为Ma0x,
对木板运用动能定理得:Ma0x+W= (1分)
(1分)
解得W=-3.0 J,说明此时弹簧的弹性势能Ep=3.0 J(1分)
(3)金属块和木板达到共速后压缩弹簧,速度减小为0后反向弹回,设弹簧恢复原长时木板和金属块的速度为v3,在此过程中对木板和金属块,由能量的转化和守恒得:
Ep-(F2+Mgsin θ+mgsin θ)x= (M+m)
(M+m) -
- (M+m)
(M+m) (2分)
(2分)
木板离开弹簧后,设滑行距离为s,由动能定理得:
-(M+m)g(μ2cos θ+sin θ)s=- (M+m)
(M+m) (2分)
(2分)
解得s=0.077 m(1分)
考点:考查了动能定理,能量守恒定律,牛顿第二定律,运动学公式
本题难度:困难
3、计算题 如图所示,一个放置在水平地面上的木块,其质量为m=2kg,受到一个斜向下的、与水平方向成30o角的推力F=10N的作用,使木块从静止开始运动,5s后撤去推力。若木块与地面间的动摩擦因数μ=0.1,求木块在地面上运动的总位移。(g=10m/s2, )
)
参考答案:
本题解析:
根据正交分解牛顿第二定律可得: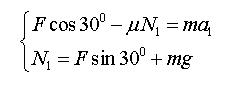
解得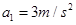
根据匀变速直线运动规律可得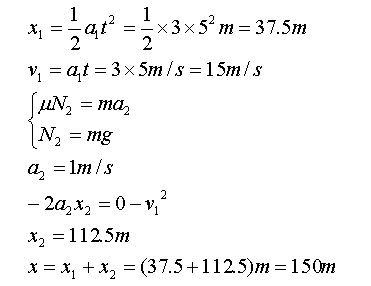
考点:考查了牛顿第二定律与运动学公式的应用
本题难度:一般
4、计算题 如图所示,物块Α、Β用一劲度系数为k=200N/m的轻弹簧相连静止于水平地面上,Α物体质量mA=2kg, Β物体质量mB="4Kg." 现用一恒力F=30N竖直向上拉物体A, 使Α从静止开始运动,当Α运动到最高点时Β刚好要离开地面但不能继续上升。若弹簧始终处于弹性限度内,取g = 10m/s2。求:
(1)Β刚要离开地面时,拉力F做的功;
(2)Β刚要离开地面时Α的加速度大小;
(3)从Α开始运动到Α到达最高点的过程中弹簧弹力对Α做的功。
参考答案:(1)9J(2)-15m/s2(3)-3J
本题解析:(1)未加拉力时弹簧缩短量为x1
Kx1=mAg ①
B刚要离地时弹簧伸长量为x2。kx2=mBg ②
设拉力F做功W1 W1=F(x1+x2) ③ 解得:W1=9J ④
(2)B刚要离地时,对A,根据牛顿第二定律可得:F-mAg-kx2=mAaA ⑤
解得:aA=-15m/s2 ⑥
(3)设弹簧对A做的功W弹,对A根据动能定理可得:W1+W弹-mAg(x1+x2)=0 ⑦
解得:W弹=-3J ⑧
考点:本题考查了牛顿第二定律和动能定理的应用。
本题难度:一般
5、计算题 (10分)如图所示,一半径为R=0.5m的半圆型光滑轨道与水平传送带在B点连接,水平传送带AB长L="8" m,向右匀速运动的速度为v0。一质量为1 kg的小物块(可视为质点)以v1="6" m/s的初速度从传送带右端B点向左冲上传送带,物块再次回到B点后恰好能通过圆形轨道最高点,物块与传送带间的动摩擦因数μ=0.45,g取10 m/s2。求物块相对地面向左运动的最大距离x及传送带的速度大小v0。
参考答案:4m;5m/s
本题解析:(1)物块向左匀减速至速度为零时,相对地面向左的位移最大。
根据运动学公式: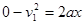
根据牛顿第二定律:物块加速度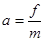
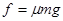
联立各式,代入数据解得: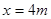
(2)物块恰过最高点(设为C点),临界条件:
从B到C的过程,物块机械能守恒: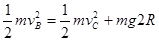
代入数据解得: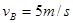
由题意可知,物块在传送带上匀减速至速度为零后反向向右匀加速运动直到与传送带速度相等,再匀速运动。故传送带速度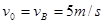
考点:牛顿定律;机械能守恒定律;圆周运动的规律。
本题难度:困难