时间:2017-09-25 08:09:13
1、计算题 如图所示，在平面直角坐标系xOy内，第Ⅰ象限存在沿y轴负方向的匀强电场，第Ⅳ象限以ON为直径的半圆形区域内，存在垂直于坐标平面向外的匀强磁场，磁感应强度为B。一质量为m、电荷量为q的带正电的粒子，从y轴上y＝h处的M点，以速度v0垂直于y轴射入电场，经x轴上x＝2h处的P点进入磁场，最后以垂直于y轴的方向射出磁场。不计粒子重力。求：
（1）在原图上画出粒子在电场和磁场中运动轨迹示意图；
（2）电场强度大小E ；
（3）粒子在磁场中运动的轨道半径r；
（4）粒子从进入电场到离开磁场经历的总时间t。 
参考答案：解：（1）粒子的运动轨迹如图所示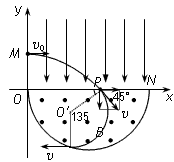 
（2）设粒子在电场中运动的时间为t1
x、y方向：2h＝v0t1，h＝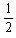
at
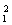
根据牛顿第二定律：Eq＝ma
求出E＝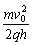
（3）根据动能定理：Eqh＝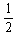
mv2－
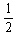mv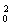
将E的表达式代入上式，可求出v＝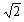
v0
再根据Bqv＝m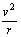
，求出 r＝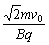
（4）粒子在电场中运动的时间：t1＝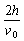
粒子在磁场中运动的周期：T＝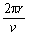
＝
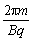
根据粒子入射磁场时与x轴成45°，射出磁场时垂直于y轴，可求出粒子在磁场中运动的圆弧所对的圆心角为135°
设粒子在磁场中运动的时间为t2＝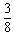
T
求出t＝t1＋t2＝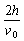
＋
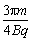
本题解析：
本题难度：困难
2、计算题 某探究小组设计了一个质谱仪，其原理如图所示.一束电量均为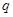
，质量不同的带负电的粒子，经过电场加速后进入一速度选择器，从
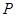点进入一等腰直角三角形的有界磁场中，又从斜边射出.速度选择器中垂直纸面向里的匀强磁场的磁感应强度为
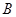，竖直向下的匀强电场强度为
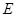，有界磁场的磁感应强度为
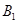，直角边长为
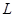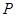，为斜边的中点，
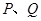两点相距为
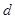.求：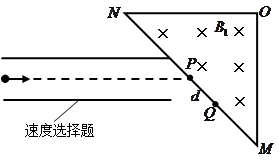
（1）带电粒子进入有界磁场的速度大小.
（2）带电粒子质量应满足的条件.
（3）打在斜边上Q点的带电粒子在磁场中运动的时间.
参考答案：（1）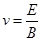
?（2）
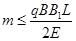?（3）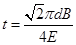
本题解析：（1）设速度为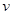
，在速度选择器中，有：
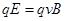?① （3分）
带电粒子进入有界磁场的速度为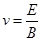 ②（2分）
（2）设带电粒子质量为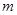
，在有界磁场中做圆周运动半径为
，
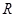根据牛顿第二定律有；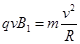
③ （3分）
要使带电粒子从斜边射出，必有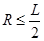
④ （2分）
由②③④得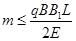：? ⑤ ?（2分）
（3）根据几何关系可得，带电粒子在磁场中运动的半径为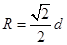
?⑥ （2分）
带电粒子在磁场中运动的周期：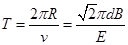
?⑦ （2分）
带电粒子在磁场中运动的时间为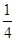
周期：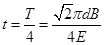
⑧ （2分）
本题难度：一般
3、计算题 如图所示的装置，左半部为速度选择器，右半部为匀强的偏转电场。一束同位素离子流从狭缝S1射入速度选择器，能够沿直线通过速度选择器并从狭缝S2射出的离子，又沿着与电场垂直的方向，立即进入场强大小为E的偏转电场，最后打在照相底片D上。已知同位素离子的电荷量为q(q>0)，速度选择器内部存在着相互垂直的场强大小为E0的匀强电场和磁感应强度大小为B0的匀强磁场，照相底片D与狭缝S1、S2的连线平行且距离为L，忽略重力的影响。
(1)求从狭缝S2射出的离子速度v0的大小；
(2)若打在照相底片上的离子在偏转电场中沿速度v0方向飞行的距离为x，求出x与离子质量m之间的关系式（用E0、B0、E、q、m、L表示）。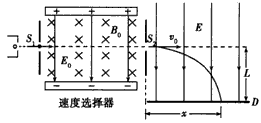
参考答案：解：(1)能从速度选择器射出的离子满足qE0=qv0B0 ①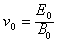
?②
(2)离子进入匀强偏转电场E后做类平抛运动，则
x=v0t ③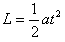
?④
由牛顿第二定律得qE=ma ⑤
由②③④⑤解得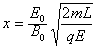
本题解析：
本题难度：一般
4、计算题 如图所示，光滑水平面上有一质量为m、带正电荷量为q的物块，在水平方向互相垂直的匀强电磁复合场中由静止释放，已知电场强度为E，磁感应强度为B。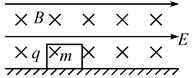
求：物块在水平面上滑行的时间。
参考答案：m2g/q2EB
本题解析：物块受力如图。
故物块先做匀加速运动，速度v增大则f洛＝qvB亦随之增大
由竖直方向受力做FN＝mg－qvB，即FN逐渐减小，
当FN＝0时，物块将离开水平面，此时：
mg＝qvB? ①
v＝at＝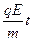
? ②
由①?②?得 t＝m2g/q2EB
本题难度：简单
5、选择题 右图中MN、GH为足够长光滑平行金属导轨，金属棒AB、CD垂直放在两导轨上，整个装置在同一水平面内。匀强磁场垂直于导轨所在的平面，方向如图。若给CD杆一个水平向右的速度，则
A．AB、CD最终都处于静止状态
B．AB、CD最终以相同的速度保持匀速直线运动状态
C．AB、CD最终保持匀速直线运动状态，但vCD> vAB
D．AB、CD不断做往复运动
参考答案：B
本题解析：根据电磁感应定律和牛顿第二定律:对AB棒有：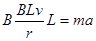
对CD棒有：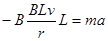
一个加速一个减速，当二者共速时，磁通量不变，没有感应电动势产生，不再受安培力，二者将匀速运动。所以选B.
本题难度：简单