时间:2017-09-25 08:09:13
1、计算题 某探究小组设计了一个质谱仪，其原理如图所示.一束电量均为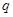
，质量不同的带负电的粒子，经过电场加速后进入一速度选择器，从
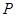点进入一等腰直角三角形的有界磁场中，又从斜边射出.速度选择器中垂直纸面向里的匀强磁场的磁感应强度为
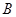，竖直向下的匀强电场强度为
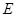，有界磁场的磁感应强度为
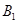，直角边长为
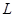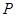，为斜边的中点，
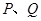两点相距为
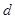.求：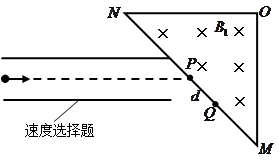
（1）带电粒子进入有界磁场的速度大小.
（2）带电粒子质量应满足的条件.
（3）打在斜边上Q点的带电粒子在磁场中运动的时间.
参考答案：（1）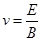
?（2）
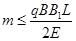?（3）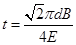
本题解析：（1）设速度为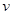
，在速度选择器中，有：
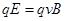?① （3分）
带电粒子进入有界磁场的速度为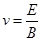 ②（2分）
（2）设带电粒子质量为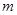
，在有界磁场中做圆周运动半径为
，
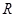根据牛顿第二定律有；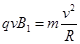
③ （3分）
要使带电粒子从斜边射出，必有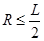
④ （2分）
由②③④得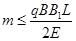：? ⑤ ?（2分）
（3）根据几何关系可得，带电粒子在磁场中运动的半径为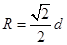
?⑥ （2分）
带电粒子在磁场中运动的周期：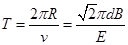
?⑦ （2分）
带电粒子在磁场中运动的时间为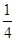
周期：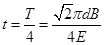
⑧ （2分）
本题难度：一般
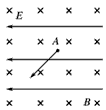
2、选择题 如图所示，质量为m，带电荷量为－q的微粒以速度v与水平方向成45°角进入匀强电场和匀强磁场，磁场方向垂直纸面向里。如果微粒做匀速直线运动，则下列说法正确的是
[? ]
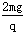
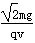
参考答案：AD
本题解析：
本题难度：一般
3、计算题 如图所示，在MN左侧有相距为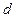
的两块正对的平行金属板P、Q，板长
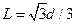两板带等量异种电荷，上极板带负电。在MN右侧存在垂直于纸面的矩形匀强磁场(图中未画出)，其左边界和下边界分别与MN、AA’重合(边界上有磁场)。现有一带电粒子以初速度v0沿两板中央OO′射入，并恰好从下极板边缘射出，又经过在矩形有界磁场中的偏转，最终垂直于MN从A点向左水平射出。 已知A点与下极板右端的距离为d。不计带电粒子重力。求：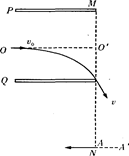
小题1:粒子从下极板边缘射出时的速度；
小题2:粒子从O运动到A经历的时间；
小题3:矩形有界磁场的最小面积。
参考答案：
小题1:
小题2: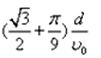
小题3: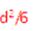
本题解析：(1)带电粒子在电场中平行极板方向匀速运动：
? (1分)
竖直方向从静止开始做匀加速运动：
本题难度：一般
4、选择题 如图所示，带电粒子以水平速度v0垂直进入正交的匀强电场和匀强磁场区域中，穿出电磁场区域时速度为v，电场强度为E，磁感应强度为B，则粒子的径迹、v与v0的大小关系为（ ）
A．要使粒子能沿直线运动，正电荷应从左边射入，负电荷应从右边射入
B．当v0=
| E B |
| E B |
| E B |
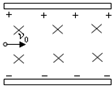
参考答案：A、若是正电荷，从左端进入复合场，则洛伦兹力向上，电场力向下．如电场力与洛伦兹力等大，则能沿直线通过；若是负电荷，从左端进入复合场洛伦兹力向下，电场力向上，若等大则也可以沿直线通过．故A错误．
B、如粒子沿直线通过，电场力与洛伦兹力等大反向，由有qE=Bqv0，即v0=EB．所以当v0=EB沿直线穿过，又因为在复合场中运动时洛伦兹力不做功，粒子沿电场方向无位移，故电场力也不做功，故v=v0，故B正确．
C、当v0＜EB，洛伦兹力小于电场力，正电荷粒子会向上偏，即沿电场方向上有位移．电场力对离子做正功，所以v＞v0，故C正确．
D、当v0＞EB时，洛伦兹力大于电场力，粒子将向下运动，故D错误．
故答案为：BC
本题解析：
本题难度：一般
5、选择题 带电粒子以速度v沿CB方向射入一横截面为正方形的区域．C、B均为该正方形两边的中点，如图13所示，不计粒子的重力．当区域内有竖直方向的匀强电场E时，粒子从A点飞出，所用时间为t1；当区域内有垂直于纸面向里的磁感应强度为B的匀强磁场时，粒子也从A点飞出，所用时间为t2，下列说法正确的是( )
A．t1<t2?B．t1>t2?
C.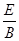
＝
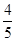v?D.＝
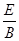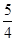v
参考答案：AD
本题解析：带电粒子在匀强电场中做类平抛运动，水平方向上做匀速运动，而在匀强磁场中做匀速圆周运动，水平方向上做减速运动，所以t2>t1，A项正确，B项错；设正方形区域的边长为l，则当加电场时，有l＝vt1和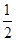
＝
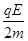t12，得E＝
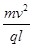.当加磁场时，根据几何关系，有(R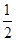－)2＋l2＝R2，得R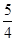＝l，再由R＝
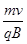得B＝
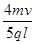.所以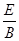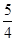＝v，D项对，C项错．
本题难度：简单