时间:2017-09-23 23:45:34
1、简答题 汽车以10m/s的速度通过一座拱桥的最高点，拱桥半径20m，求此车里的一名质量为20kg的小孩对座椅的压力．（g=10m/s2）
参考答案：人受重力和支持力，合力提供向心力，根据牛顿第二定律，有：
mg-N=mv2r；
代入数据，解得：N=100N；
根据牛顿第三定律，人对座椅的压力与座椅对人的支持力等值、反向、共线，故压力100N；
答：里的一名质量为20kg的小孩对座椅的压力为10N．
本题解析：
本题难度：一般
2、简答题 长L=0.5m、质量可忽略的杆，其一端固定于O点，另一端连有质量m=2kg的小球，它绕O点在竖直平面内做圆周运动．当通过最高点时，如图所示，求下列情况下，杆受到的力（计算出大小，并说明是拉力还是压力，g取10m/s2）：
（1）当v=1m/s时，杆受到的力多大，是什么力？
（2）当v=4m/s时，杆受到的力多大，是什么力？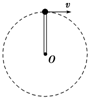
参考答案：对小球受力分析，假设杆子对小球的作用力方向竖直向上大小为F：
根据牛顿第二定律：mg-F=mv2L
（1）当v=1m/s时，解得：F=mg-mv2L=16N
故杆子对小球的作用力大小为16N，方向向上．
根据牛顿第三定律小球对杆子的作用力为向下的压力，大小为16N．
（2）当v=4m/s时，解得：F=mg-mv2L=-44N，负号表示力F的方向与题目假设的方向相反，
故杆子对小球的作用力大小为44N，方向向下．
根据牛顿第三定律小球对杆子的作用力为向上的拉力，大小为44N．
答：（1）当v=1m/s时，杆受到的力大小为16N，方向向上，是拉力．
（2）当v=4m/s时，杆受到的力大小为44N，方向向下，是压力．
本题解析：
本题难度：一般
3、简答题 宇航员到达某行星表面后，用长为L的细线拴一小球，让球在竖直面内做圆周运动．他测得当球通过最高点的速度为v0时，绳中张力刚好为零．设行星的半径为R、引力常量为G，求：
（1）该行星表面的重力加速度大小
（2）该行星的质量
（3）在该行星表面发射卫星所需要的最小速度．
参考答案：（1）由题意知：球在最高点只受重力作用，设小球的质量为m，
由牛顿第二定律得：mg=mv20L，解得：g=v20L? ①．
（2）对行星表面的任一物体m′所受到的重力等于物体与行星间的万有引力，
设行星质量为M，则m′g=Gm′MR2? ②，
由①②解得行星的质量M=v20R2GL
（3）对卫星，绕行星表面做圆周运动的向心力由万有引力即重力提供，
由牛顿第二定律得：mg=mv2R? ③，由①③解得：v=v0
本题解析：
本题难度：一般
4、计算题 如图所示，轻杆长2L，中点装在水平轴O点，两端分别固定着小球A和B，A、B球质量分别为m、2m，整个装置在竖直平面内做圆周运动，当杆绕O转动到某一时刻，A球到达最高点，此时球A与杆之间恰好无相互作用力，求此时O轴所受力的大小和方向。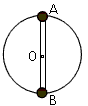 
参考答案：解：设图示位置A、B两球速率为V，且杆对B球的作用力为F，即O轴所受作用力为F，则：
? 对A球有：mg=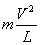
…… （1）
? 对B球有：F－2mg =2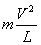
…… （2）
? 由（1）（2）可求得：F=4mg
本题解析：
本题难度：一般
5、选择题 如图所示光滑管形圆轨道半径为R（管径远小于R），小球a、b大小相同，质量均为m，其直径略小于管径，能在管中无摩擦运动．两球先后以相同速度v通过轨道最低点，且当小球a在最低点时，小球b在最高点，以下说法正确的是（ ）
A．当小球b在最高点对轨道无压力时，小球a比小球b所需向心力大5mg
B．当v=
| gR |
| 5GR |
| 5gR |
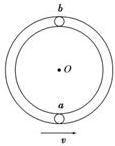
参考答案：由于管中没有摩擦力的作用，所以球的机械能守恒，
当小球b在最高点对轨道无压力，即只有重力做为向心力，
所以mg=mvb2R，所以在最高点时b球的速度的大小为
本题解析：
本题难度：简单