时间:2017-09-23 23:45:34
1、选择题 如图,在电机距轴O为r的处固定一质量为m的铁块,电机启动后,铁块以角速度ω绕O轴匀速转动,则电机对地面最大压力和最小压力之差为( )
A.mω2?r
B.2mω2?r
C.mg+2mω2?r
D.2mg+2mω2r
参考答案:在最低点时,根据牛顿第二定律得,F-mg=mrω2,解得F=mg+mrω2,此时电机对地面的压力最大,N=Mg+F=Mg+mg+mrω2.
在最高点,根据牛顿第二定律得,mg+F′═mrω2,解得F′=mrω2-mg.此时电机对地面的压力最小,N′=Mg-F′=Mg+mg-mrω2.
则压力之差△F=N-N′=2mω2 r.故B正确,A、C、D错误.
故选B.
本题解析:
本题难度:简单
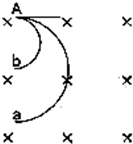
2、选择题 如图所示,a和b是从A点以相同的动能射入匀强磁场的两个带等量电荷的粒子运动的半圆形径迹,已知ra=2rb,则由此可知( )
A.两粒子均带正电,质量比
| ma mb |
| ma mb |
| ma mb |
| 1 4 |
| ma mb |
| 1 4 |
参考答案:
两粒子进入磁场后均向下偏转,可知在A点,均受到向下的洛伦兹力,由左手定则可知,四指所指的方向与运动方向相反,得知两个粒子均带负电;
由动能和动量之间的关系有:P=
本题解析:
本题难度:简单
3、选择题 两个带异种电荷的点电荷M、N质量分别为m1、m2(m1>m2),电荷量的绝对值分别是q1、q2(q1<q2).在库仑力作用下,M、N将以两者连线上的某一点O为圆心做匀速圆周运动.以下说法中正确的是( )
A.M所受到的向心力比N所受到的向心力小
B.它们做圆周运动的周期相等
C.它们做圆周运动的线速度与它们的质量成反比
D.它们做圆周运动的半径与它们的电荷量成反比
参考答案:A、对于质量m1,它们的库仑力提供其向心力.即kq1q2?r2=m1ω2r1=m2ω2r2.应该是相等的,故A错误
B、两异种点电荷能绕圆心各自做匀速圆周运动,它们的角速度相同,故B正确
C、根据v=rω得它们的线速度与质量成反比,故C正确
D、由上式得r1r2=m2m1 所以它们的半径与质量成反比,与它们的电荷量无关,故D错误
故选BC.
本题解析:
本题难度:一般
4、简答题 如图所示,在E=103V/m的水平向左匀强电场中,有一光滑半圆形绝缘轨道竖直放置,轨道与一水平绝缘轨道MN连接,半圆轨道所在竖直平面与电场线平行,其半径R=40cm,一带正电荷q=10-4C的小滑块质量为m=40g,与水平轨道间的动摩擦因数μ=0.2,取g=10m/s2,问:
(1)要小滑块能运动到圆轨道的最高点C,滑块应在水平轨道上离N点多远处释放?
(2)这样释放的滑块通过P点时对轨道压力是多大?(P为半圆轨道中点)
(3)小滑块经过C点后最后落地,落地点离N点的距离多大?落地时的速度是多大?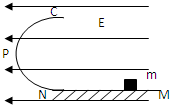
参考答案:(1)设滑块与N点的距离为L,
分析滑块的运动过程,由动能定理可得,
qEL-μmgL-mg?2R=12mv2-0
小滑块在C点时,重力提供向心力,
所以 mg=mv2R
代入数据解得 v=2m/s,L=20m.
(2)滑块到达P点时,对全过程应用动能定理可得,
qE(L+R)-μmgL-mg?R=12mvP2-0
在P点时由牛顿第二定律可得,
N-qE=mv2PR
解得N=1.5N?
由牛顿第三定律可得,滑块通过P点时对轨道压力是1.5N.
(3)小滑块经过C点,在竖直方向上做的是自由落体运动,
由2R=12gt2可得滑块运动的时间t为,
t=
本题解析:
本题难度:一般
5、选择题 如图所示,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做圆周运动,通过最高点时,由于球对杆有作用,使杆发生了微小形变,关于杆的形变量与球在最高点时的速度大小关系,正确的是

[? ]
参考答案:C
本题解析:
本题难度:一般