时间:2017-09-23 23:12:19
1、选择题 用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环，AB为圆环的一条直径。如图所示，在AB的左侧存在一个均匀变化的匀强磁场，磁场垂直圆环所在平面，方向如图所示，磁感应强度大小随时间的变化率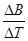
?＝k（k<0）。则（ ）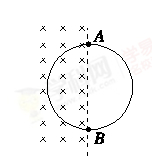
A．圆环中产生逆时针方向的感应电流
B．圆环具有扩张的趋势
C．圆环中感应电流的大小为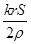
D．圆环具有收缩的趋势
参考答案：B
本题解析：
试题分析: 磁场方向垂直纸面向里，磁感应强度大小随时间的变化率ΔB/Δt＝k（k<0），说明B减少，穿过圆环的磁通量减少，由楞次定律判断可知：圆环中产生的感应电流方向沿顺时针方向，故A错误．穿过圆环的磁通量减少，由楞次定律可知，圆环为了阻碍磁通量的减少，圆环应有扩展的趋势，故B正确，D错误；
C、由法拉第电磁感应定律得E=Δφ/Δt=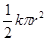
，圆环的电阻R=ρ
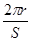，则感应电流大小为 I=
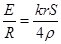，故C错误．
本题难度：简单
2、选择题 两根光滑的金属导轨，平行放置在倾角为θ的斜面上，导轨的左端接有电阻R，导轨的电阻可忽略不计．斜面处在匀强磁场中，磁场方向垂直于斜面向上．质量为m，电阻可不计的金属棒ab在沿着斜面与金属棒垂直的拉力F作用下沿导轨匀速上滑，并上升h高度，如图所示，在这个过程中（ ? ）
A．作用在金属棒上各个力的合力所做的功等于电阻R上产生的焦耳热?
B．作用在金属棒上各个力的合力所做的功等于mgh与电阻R上产生的焦耳热之和?
C．恒力F与重力的合力所做的功等于电阻R上产生的焦耳热?
D．恒力F与安培力的合力所做的功等于零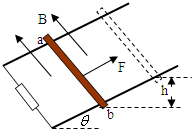
参考答案：C
本题解析：
本题难度：一般
3、简答题 在拆装某种大型电磁设备的过程中，需将设备内部的处于强磁场中的线圈先闭合，然后再提升直至离开磁场．操作时通过手摇轮轴A和定滑轮O来提升线圈．假设该线圈可简化为水平长为L，上下宽度为d的矩形线圈，其匝数为n，总质量为M，总电阻为R．磁场的磁感应强度为B，如图所示．开始时线圈的上边缘与有界磁场的上边缘平齐．若转动手摇轮轴A．在时间t内把线圈从图示位置匀速向上拉出磁场．求此过程中．
（1）流过线圈中每匝导线横截面的电量是多少？
（2）在转动轮轴时，人至少需做多少功？（不考虑摩擦影响）．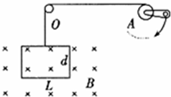
参考答案：（1）在匀速提升过程中线圈运动速度?υ=dt①
线圈中感应电动势?E=nBLυ②
产生的感应电流I=ER③流过导线横截面的电量q=I?t④
联立①②③④得q=nRLdR．
（2）匀速提拉过程中，要克服重力和安培力做功
即?W=WG+WB⑤
又WG=Mgd⑥
WB=nBILd⑦
联立①②③⑤⑥⑦可得?W=Mgd+nB2L2d2R?t．
答：（1）流过线圈中每匝导线横截面的电量是nRLdR．
（2）在转动轮轴时，人至少需做功为Mgd+nB2L2d2R?t．
本题解析：
本题难度：一般
4、简答题 在竖直面内有两平行金属导轨AB、CD，间距为L，金属棒ab可在导轨上无摩擦地滑动．棒与导轨垂直，并接触良好．它们的电阻均可不计．导轨之间有垂直纸面向外的匀强磁场，磁感强度为B．导轨右边与电路连接．电路中的三个定值电阻R1、R2、R3阻值分别为2R、R和0.5R．在BD间接有一水平放置的平行板电容器C，极板间距离为d．
（1）当ab以速度v0匀速向左运动时，电容器中质量为m的带电微粒恰好静止．试判断微粒的带电性质，及带电量的大小．
（2）当ab棒以某一速度沿导轨匀速运动时，发现带电微粒从两极板中间由静止开始向下运动，历时t=2×10-2?s到达下极板，已知电容器两极板间距离d=6×10-3m，求ab棒的速度大小和方向．（g=10m/s2）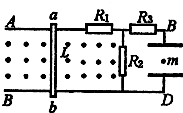
参考答案：（1）棒匀速向左运动，感应电流为顺时针方向，电容器上板带正电，板间场强向下．
∵微粒受力平衡，电场力向上，场强方向向下．
∴微粒带负电．
设微粒带电量大小为q，由平衡条件知：mg=qUCd…①
对R1、R2和金属棒构成的回路，由欧姆定律可得
? I=E3R…②
? UC=IR2=IR…③
由法拉第电磁感应定律可得 E=BLv0…④
由以上各式求得?q=3mgdBLv0…⑤
（2）因带电微粒从极板中间开始向下作初速度为零的匀加速运动，
由运动学公式得：12d=12at2…⑥
得?a=15m/s2=32g＞g…⑦
可见带电微粒受到的电场力向下，所以ab棒应向右运动，设此时极板间电压为UC′，由牛顿第二定律，得
?mg+qUC′d=m?32g…⑧
出⑤和⑧得?UC′=16BLv0
设棒ab运动速度为vx，则电动势E′=Blvx，由欧姆定律得：
?UC′=I′R2=BLvx3R?R=13BLvx=16nlv0
∴vx=12v0．即棒运动速度大小应为原来速度的一半，即为12v0．
答：
（1）微粒的带负电，带电量的大小为3mgdBLv1．
（2）ab棒的速度大小为12v0，方向向右．
本题解析：
本题难度：一般
5、简答题 如图所示，两根足够长的光滑平行金属导轨MN、PQ间距离L=0.5m，其电阻不计，两导轨及其构成的平面与水平面成30°角．完全相同的两金属棒ab、cd分别垂直导轨放置，且都与导轨始终有良好接触．已知两金属棒质量均为m=0.02kg，电阻相等且不可忽略．整个装置处在垂直于导轨平面向上的匀强磁场中，磁感应强度B=0.2T，金属棒ab在平行于导轨向上的力F作用下，沿导轨向上匀速运动，而金属棒cd恰好能够保持静止．取g=10m/s2，求：
（1）通过金属棒cd的电流大小、方向；
（2）金属棒ab受到的力F大小；
（3）若金属棒cd的发热功率为0.1W，金属棒ab的速度．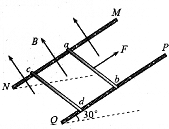
参考答案：（1）金属棒cd受到的安培力：Fcd=BIL，
金属棒cd静止处于平衡状态，由平衡条件得：Fcd=mgsin30°，
即：BIL=mgsin30°，电流为I=mgsin37°BL=0.02×10×0.50.2×0.5=1A；
由右手定则可知，通过ab棒的电流由a流向b，则金属棒cd中的电流方向由d至c；
（2）金属棒ab与cd受到的安培力大小相等：Fab=Fcd=BIL=0.2×1×0.5=0.1N
金属棒ab做匀速直线运动，处于平衡状态，由平衡条件得：
F=mgsin30°+Fab=0.02×10×0.5+0.1=0.2N；
（3）金属棒发热功率：P=I2R，
金属棒电阻：R=PI2=0.1W(1A)2=0.1Ω，
金属棒ab切割磁感线产生的 感应电动势：E=BLv，
由闭合电路欧姆定律得：I=E2R=BLv2R，
金属棒的速度：v=2IRBL=2×1A×0.1Ω0.2T×0.5m=2m/s；
答：（1）通过金属棒cd的电流大小为1A，方向：由d流向c；
（2）金属棒ab受到的力F大小为0.2N；
（3）金属棒ab的速度为2m/s．
本题解析：
本题难度：一般