时间:2017-08-22 02:37:29
1、简答题 如图,在竖直平面内有一固定光滑轨道,BD是水平直轨道,BC是圆心为O、半径为R的
| 1 2 |
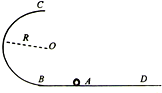
参考答案:(1)小滑块恰好通过最高点,则有:mg=vC2R
解得:vC=
本题解析:
本题难度:一般
2、选择题 飞机驾驶员最多可承受9倍的重力加速度带来的影响,当飞机在竖直平面上沿圆弧轨道俯冲时速度为v,则圆弧的最小半径为( )
A.
| v2 9g |
| v2 8g |
| v2 7g |
| v2 g |
参考答案:当飞机飞到最低点时,由牛顿第二定律得:
F-mg=mv2R;
由题意,得到:F≤9mg;
解得:R≥v28g;
故选B.
本题解析:
本题难度:一般
3、选择题 如图所示,小球m在竖直放置的光滑圆形管道内做圆周运动,下列说法中正确的是( )
A.小球通过最高点的最小速度为
| gR |
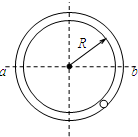
参考答案:A、在最高点,由于外管或内管都可以对小球产生弹力作用,当小球的速度等于0时,内管对小球产生弹力,大小为mg,故最小速度为0,故A错误;
B、小球在圆形轨道的最高点,重力G和弹力N(假设向下)的合力提供向心力,根据牛顿第二定律,有mg+F=mv2R,F=mv2R-mg,
①当v<
本题解析:
本题难度:简单
4、简答题 如图所示,OA、OB两根绳子系着一个质量为m=0.5Kg的小球,两绳的A、B端分别固定在竖直转动轴上,OA绳长L=2m,两绳都拉直时与轴的夹角分别为370和530,(sin37°=0.6?cos37°=0.8?g=10m/s2)?求:
(1)小球随轴转动的角速度ω=2.4rad/s时,绳OA、OB的张力分别是多少?
(2)小球随轴转动的角速度ω=3.0rad/s时,绳OA、OB的张力分别是多少?
参考答案:(1)若OB绳子刚好伸直,则:
mgtan37°=m(Lsin37°)ω02
解得:ω0=2.5rad/s
当ω=2.4rad/s<ω0时,OB绳子是弯曲的;
故OB绳子张力为零;
根据牛顿第二定律,有:
TOAx=m(Lsin37°)ω2=3.456N;
TOAy=mg=5N;
TOA=
本题解析:
本题难度:一般
5、选择题 质量为m的物体沿着半径为r的半球形金属球壳滑到最低点时的速度大小为υ,如图所示,若物体与球壳之间的摩擦因数为μ,则物体在最低点时的 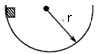
[? ]
A.向心加速度为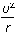
B.向心力为m(g+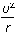 )?
)?
C.对球壳的压力为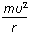 ?
?
D.受到的摩擦力为μm(g+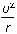 )?
)?
参考答案:ABD
本题解析:
本题难度:一般