时间:2017-08-22 02:05:31
1、简答题 如图甲所示，足够长平行金属导轨倾斜放置，倾角为37°，宽度为0.5m，电阻忽略不计，其上端接一小灯泡，电阻为1Ω．质量为0.2kg的导体棒MN垂直于导轨放置，距离顶端1m，接入电路的电阻为1Ω，两端与导轨接触良好，与导轨间的动摩擦因数为0.5．在导轨间存在着垂直于导轨平面向下的匀强磁场，磁感应强度随时间变化的规律如图乙所示．先固定导体棒MN，2s后让MN由静止释放，运动一段时间后，小灯泡稳定发光．重力加速度g取10m/s2，sin37°=0.6．求
（1）1s时流过小灯泡的电流大小和方向；
（2）小灯泡稳定发光时消耗的电功率；
（3）小灯泡稳定发光时导体棒MN运动的速度．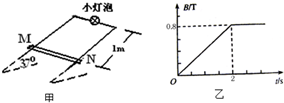
参考答案：（1）由图知，△B△t=0.4T/s
根据法拉第电磁感应定律得在0-2s内回路中产生的感应电动势 E=△B△tS=0.82×0.5×1V=0.2V
感应电流的大小 I=ER灯+RMN=0.21+1A=0.1A
根据楞次定律判断可知，回路中电流的方向沿逆时针．
（2）、（3）2s后，当MN棒匀速直线运动时达到稳定状态，设稳定时速度为v．
则产生的感应电动势为 E′=BLv
感应电流 I′=E′R灯+RMN
MN棒所受的安培力大小 F=BI′L，方向沿轨道向上．
联立得：F=B2L2vR灯+RMN
MN棒匀速运动时，受力平衡，则有：F+μmgcos37°=mgsin37°
由上两式得：B2L2vR灯+RMN+μmgcos37°=mgsin37°
将B=0.8T，L=0.5m，R灯=1Ω，RMN=1Ω，μ=0.5，m=0.2kg
代入解得：v=5m/s
则得：I′=E′R灯+RMN=BLvR灯+RMN=0.8×0.5×51+1A=1A
小灯泡稳定发光时消耗的电功率 P=I2R灯=12×1W=1W
答：（1）1s时流过小灯泡的电流大小是0.1A，方向逆时针．（2）小灯泡稳定发光时消耗的电功率是1W．（3）小灯泡稳定发光时导体棒MN运动的速度是5m/s．
本题解析：
本题难度：一般
2、选择题 如图甲所示，n=50匝的圆形线圈M，它的两端点a、b与内阻很大的电压表相连，线圈中磁通量的变化规律如图乙所示，则a、b两点的电势高低与电压表的读数为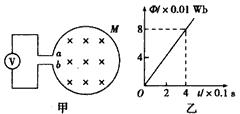 
[? ]
A．φa>φb，20 V
B．φa>φb，10 V?
C．φa<φb，20 V
D．φa<φb，10 V
参考答案：B
本题解析：
本题难度：一般
3、选择题 用相同导线绕制的边长为L或2L的四个闭合导体线框，以相同的速度匀速进入右侧匀强磁场，如图所示．在每个线框进入磁场的过程中，M、N两点间的电压分别为Ua、Ub、Uc和Ud．下列判断正确的是（ ）（所有长边是2L ,短边是L）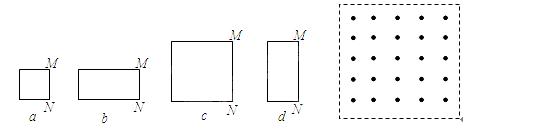
A．
B．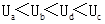
C．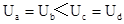
D．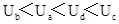
参考答案：B
本题解析：线框进入磁场后切割磁感线，a、b产生的感应电动势是c、d电动势的一半，而不同的线框的电阻不同，设a线框电阻为4r，b、c、d线框的电阻分别为6r、8r、6r，所以：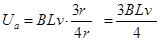
，
，
，
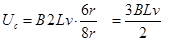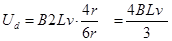；所以满足
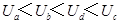
故选B
考点：导体切割磁感线时的感应电动势
点评：对于这类电磁感应与电路的结合的问题，弄清哪部分是电源以及与外电路的串并联情况，然后根据闭合电路欧姆定律进行求解
本题难度：一般
4、计算题 一个用绝缘材料制成的扁平薄圆环，其内、外半径分别为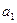
、
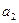，厚度可以忽略。两个上下表面都带有电荷，每个面的电荷面密度
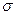为已知常量。薄圆环绕通过环心垂直环面的轴以
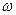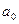
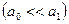转动。将一半径为
、电阻为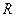
并与薄圆环共面的导线圆环与薄圆环同心放置。试求：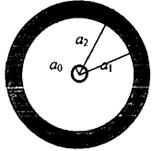
（1）薄圆环转动时在圆心处产生的磁感应强度为多少？
（2）若薄圆环以大小不变的角加速度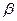
减速转动，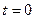
时刻的角速度为
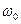，在薄圆环减速运动过程中导线圆环中的感应电动势为多少？
提示：（1）角加速度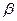表示单位时间里角速度的变化量。
（2）半径为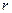
、通有电流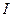
的圆线圈（环形电流），在圆心处产生的磁感应强度为
（
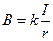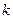为已知常量）
参考答案：（1）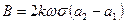
（2）
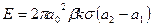
本题解析：略
本题难度：简单
5、简答题 如图所示，电阻忽略不计的两根两平行光滑金属导轨竖直放置，其上端接一阻值为3Ω的电阻R．在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B，磁场区域的高度为d=0.5m．导体棒a的质量ma=0.2kg、电阻Ra=3Ω；导体棒b的质量mb=0.1kg、电阻Rb=6Ω，它们分别从图中M、N处同时由静止开始沿导轨向下滑动，且都能匀速穿过磁场区域，当b?刚穿出磁场时a正好进入磁场．（不计a、b之间的作用）求：
（1）在整个过程中，a棒和b棒分别克服安培力做了多少功？
（2）在b穿过磁场区域过程中，电阻R产生的电热；
（3）M点和N点距L1的高度分别为多少？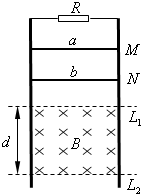
参考答案：（1）因为两金属棒都是匀速穿过磁场的，所以安培力与重力等大，克服安培力做功分别为：Wa=magd=0.2×10×0.5J=1J
? Wb=mbgd=0.1×10×0.5J=0.5J
（2）设b切割磁感线时，其上电流为I，则电阻R和a棒上电流均为12I，根据焦耳定律：Q=I2Rt得：
? Qb：Qa：QR=I2Rbt：(I/2)2Rat：(I/2)2Rt=8：1：1
由（1）知b棒穿过磁场过程产生的总电热为Q=0.5J
所以：QR=18+1+1Q=0.05J
（3）b在磁场中匀速运动时：速度为υb，总电阻R1=7.5Ω．
b中的电流Ib=BLυbR1①
由以上各式得：B2L2υbR1=mbg②
a在磁场中匀速运动时：速度为va，总电阻R2=5Ω．
对a棒同理有：B2L2υaR2=mag③
由②③式得，υbυa=34④
又：υa=υb+gt⑤d=υbt⑥
由④⑤⑥得：v2a=16gd3，v2b=3gd
所以：ha=v2a2g=83d=83×0.5m≈1.33m
hb=v2b2g=1.5d=1.5×0.5m=0.75m
答：（1）在整个过程中，a棒和b棒分别克服安培力做功1J和0.5J．
（2）在b穿过磁场区域过程中，电阻R产生的电热是0.05J；
（3）M点和N点距L1的高度分别为1.33J和0.75J．
本题解析：
本题难度：一般