时间:2016-06-23 08:44:37
1、甲、乙沿同一公路相向而行,甲的速度是乙的1.5倍,已知甲上午8点经过邮局,乙上午10点经过邮局。问:甲乙在中途何时相遇?_____
A: 8点48分 B: 8点30分 C: 9点 D: 9点10分
参考答案: A 本题解释:A。【解析】设乙的速度为x,甲就是1.5x,当甲8点到邮局时,乙离邮局还有2个小时的路程(2x),甲乙走完2x路程需要2x/(1.5x+x)=4/5小时=48分钟,加上8点,就是8点48分相遇。
2、3×999+8×99+4×9+8+7的值是:_____
A: 3840B: 3855C: 3866D: 3877
参考答案: A 本题解释:A。四个选项尾数各不相同,可考虑结果的尾数。7+2+6+8+7=30,所以尾数为0,故选A。
3、一车行共有65辆小汽车,其中45辆有空调,30辆有高级音响,12辆兼而有之。既没有空调也没有高级音响的汽车有几辆?_____
A: 2B: 8C: 10D: 15
参考答案: A 本题解释: A 【解析】做这样的题最好用画图法。
4、甲、乙、丙三人的平均年龄是26岁,除去丙后,甲、乙两人平均年龄是24岁,丙的年龄是多少岁?_____
A: 26B: 28C: 30D: 32
参考答案: C 本题解释:C解析:设甲、乙、丙年龄分别为x、y、z,根据题意得:(x+y+z)/3=26(x+y)/2=24,解得:z=30,选C。
5、某班有50位同学参加期末考试,结果英文不及格的有15人,数学不及格的有19人,英文和数学都及格的有21人。那么英文和数学都不及格的有_____人。
A: 4B: 5C: 13D: 17
参考答案: B 本题解释:本题正确答案为B。解析:设英文和数学都不及格的有x人,由容斥原理可得15+19-x=50-21,得x=5,故选B。
6、甲、乙两地相距100千米,张先骑摩托车从甲出发,1小时后李驾驶汽车从甲出发,两人同时到达乙地。摩托车开始速度是50千米/小时,中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟,那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 1(1/2)C: 1/3D: 2
参考答案: C 本题解释:C解析:汽车行驶100千米需100÷80=1(1/4)(小时),所以摩托车行驶了1(1/4)+1+,1/6=2(5/12)(小时)。如果摩托车一直以40千米/小时的速度行驶,2(5/12)小时可行驶96(2/3)千米,与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷(50-40)=1/3(小时)。故本题选C。
7、某公司面试员工,其中五分之二的应聘者获得了职位。最终录取者的平均分比录取线高7分,落选者的平均分比录取线低13分,所有应聘者的平均分为58分,则该公司的招聘录取分数线是多少?_____
A: 60B: 63C: 65D: 69
参考答案: B 本题解释:【答案】B。解析:设招聘的录取线是X,录取者的平均分为X+7,落选者的平均分为X-13,设共有5个应聘者,则录取者2个,所以,录取者总的得分2(X+7);落选者3个,落选者总的得分3(X-13)分;所有应聘者的得分为5分,所以,58×5=2(X+7)+3(X-13),可得X=63,可知答案为B。
8、三位采购员定期去某市场采购,小王每隔9天去一次,大刘每隔6天去一次,老杨每隔7天去一次,三人星期二第一次在这里碰面,下次相会将在星期几?_____
A: 星期一B: 星期五C: 星期二D: 星期四
参考答案: C 本题解释:C解析:此题乍看上去是求9,6,7的最小公倍数的问题,但这里有一个关键词,即“每隔”,“每隔9天”也即“每10天”,所以此题实际上是求10,7,8的最小公倍数。既然该公倍数是7的倍数,那么肯定下次相遇也是星期二。(10,7,8的最小公倍数是5×2×7×4=280。280÷7=40,所以下次相遇肯定还是星期二。)
9、小鲸鱼说:“妈妈,我到您现在这么大时,您就31岁啦!”大鲸鱼说:“我像你这么大年龄时,你只有1岁。”请问小鲸鱼现在几岁?_____
A: 13B: 12C: 11D: 10
参考答案: C 本题解释: C【解析】由题意可得:设小鲸鱼有x岁,大鲸鱼为y岁,则可得出y+(y-x)=31,x-(y-x)=1,解得x=11。故选C。
10、小明今年a岁,芳芳明年(a-4)岁,再过c年,他们相差_____。
A: 4岁B: c+4岁C: 5岁D: c-3岁
参考答案: C 本题解释:【解析】不管过多少年,两人年龄差永远不会改变;今年芳芳是a-5岁,所以相差5岁,选C。
11、将1~9九个自然数分成三组,每组三个数,第一组三个数之积是48,第二组三个数之积是45,三组数字中数字之和最大是多少?_____
A: 15B: 17C: 18D: 20
参考答案: C 本题解释:【答案】C。解析:显然要对48和45进行乘法拆分,显然45的可拆分情况较少,故先拆分45=1×5×9,由此可知48=2×3×8=2×4×6两种拆分情况,由此可知第三组三个数对应48的拆分也有两种情况:4、6、7;3、7、8。于是可知三组数字中加和最大的一组为3、7、8,加和为18。故正确答案为C。
12、1.31×12.5×0.15×16的值是_____。
A: 39.3B: 40.3C: 26.2D: 26.31
参考答案: A 本题解释:答案:A【解析】本式可写为1.31×12.5×4×0.15×4。
13、一个质数的3倍与另一个质数的2倍之和等于20,那么这两个质数的和是_____。
A: 8 B: 9 C: 7 D: 6
参考答案: B 本题解释:【解析】B。 设这两个质数分别为x、y,则3x+2y=20。2y和20都是偶数,则3x也是偶数,即x为偶数。又因为x同时是质数,则x=2,y=7。两质数之和x+y=9。故选B。
14、一根钢管,如果把它锯成4段,需要24分钟。照此速度,如果将它锯成8段,需要多长时间?_____
A: 42分钟B: 48分钟C: 56分钟D: 64分钟
参考答案: C 本题解释:【答案】C。解析:把一根钢管锯成4段有3个切口,并且需要24分钟,一个切口需要8分钟。若将它锯成8段,将有7个切口,则一共需要7×8=56分钟。故正确答案为C。
15、南方某城市的一家企业有90%的员工是股民,80%的员工是“万元户”,60%的员工是打工仔,那么,这家企业的“万元户”中至少有多大比例是股民?_____
A: 67.5%B: 75%C: 87.5%D: 91.5%
参考答案: C 本题解释:C【解析】先假设这个企业共有员工100人,其中:90人是股民,即可知10人不是股民;80人是“万元户”,即可20人不是“万元户”;60人是打工仔。因此,“万元户”的80人至少有80-10=70人是股民,他们占全体“万元户”的70÷80×100%=87.5%。可见,本题正确答案为C。
16、一个正三角形和一个正六边形周长相等,则正六边形面积为正三角形的:_____
A: AB: BC: CD: D
参考答案: B 本题解释:答案:B.[解析]本题为几何类题目。因为正三角形和一个正六边形周长相等,又正三角形与正六边形的边的个数比为1︰2,所以其边长比为2︰1,正六边形可以分成6个小正三角形,边长为1的小正三角形面积:边长为2的小正三角形面积=1︰4。所以正六边形面积:正三角形的面积=1×6/4=1.5。所以选B。
17、
18、甲、乙两辆清洁车执行东、西城间的公路清扫任务。甲车单独清扫需要6小时,乙车单独清扫需要9小时,两车同时从东、西城相向开出,相遇时甲车比乙车多清扫15千米。问东、西两城城相距多少千米?_____
A: 60B: 75C: 90D: 135
参考答案: B 本题解释: 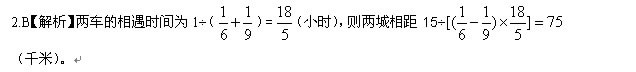
19、某旅游景点商场销售可乐,每买3瓶可凭空瓶获赠1瓶可口可乐,某旅游团购买19瓶,结果每人都喝到了一瓶可乐,该旅游团有多少人?_____
A: 19B: 24C: 27D: 28
参考答案: D 本题解释: D 解析:由题意知:买2瓶可乐就可以喝3瓶,所以19:N=2:3,N=28.5,商家不可能亏本,所以取28,选D。
20、小张每连续工作5天后休息3天,小周每连续工作7天后休息5天。假如3月1日两人都休息,3月2日两人都上班,问三月份有多少天两人都得上班?_____
A: 12B: 14C: 16D: 18
参考答案: B 本题解释:【答案】B。解析:解析1:前者8天一个循环周期,后者12天一个循环周期,两者最小公倍数为24。在三月份中从3月2日到3月25日,两人重合的工作天数为9天。在3月26日至3月31日的6天中,前5天两人同时工作。因此共计14天。故正确答案为B。解析2:用图表示如下,其中×表示工作,○表示休息,下图从3月2日起:小张:×××××○○○×××××○○○×××××○○○×××××○小周:×××××××○○○○○×××××××○○○○○××××××由图可知有14天两人都得上班。故正确答案为B。
21、将三盆同样的红花和四盆同样的黄花摆放成一排,要求三盆红花互不相邻,共有多少种不同的方法?_____
A: 8B: 10C: 15D: 20
参考答案: B 本题解释:B。【解析】四盆黄花两侧可形成5个空隙,要使三盆红花互不相邻只需从中选取3个空隙放入红花即可,=10。
22、某次考试100道选择题,每做对一题得1.5分,不做或做错一题扣1分,小李共得100分,那么他答错多少题_____
A: 20B: 25C: 30D: 80
参考答案: A 本题解释:答案:A 解析:不做或做错的题目为(100×1.5-100)÷(1.5+1)=20。
23、某工厂有学徒工、熟练工、技师共80名,每天完成480件产品的任务。已知每天学徒工完成2件,熟练工完成6件,技师完成7件,且学徒工和熟练工完成的量相等,则该厂技师人数是熟练工人数的_____倍。
A: 6 B: 8 C: 10 D: 12
参考答案: D 本题解释:D。列方程组。设学徒工、熟练工、技师分别有X,Y,Z名。则有:X+Y+Z=802X+6Y+7Z=4802X=6Y得到:X=15,Y=5,Z=60,所以Z∶Y=60∶5=12。选D。
24、0, 1, 1, 1, 2, 2, 3, 4八个数字做成的八位数,共可做成______个。_____
A: 2940B: 3040C: 3142D: 3144
参考答案: A 本题解释:A【解析】不妨先把这8个数字看作互不相同的数字,0暂时也不考虑是否能够放在最高位,那么这组数字的排列就是P(8,8),但是,事实上里面有3个1,和2个2,3个1在P(8,8)中是把它作为不同的数字排列的,那就必须从P(8,8)中扣除3个1的全排列P(3,3),因为全排列是分步完成的,在排列组合中,分步相乘,分类相加。可见必须通过除掉P(3,3)才能去掉这部分重复的数字形成的重复排列。2个2当然也是如此,所以不考虑0作为首位的情况是 P88/(P33×P22)。现在再来单独考虑0作为最高位的情况有多少种:P77/(P33×P22),最后结果就是:P88/(P33×P22)-P77/(P33×P22)=2940。
25、某年级有四个班级,不算一班有210人,不算二班有199人,不算三班有196人,不算四班有205人,问:这个年级共有_____人?
A: 240B: 270C: 320D: 3 60
参考答案: B 本题解释:B【解析】设一、二、三、四班的人数分别为a,b,c,d人。不算一班的人数是210人,即b+c+d=210;不算二班的人数是199人,即a+c+d=199;不算三班的人数是196人,即a+b+d=196;不算四班的人数为205人,即a+b+c=205;四个式子相加:3(a+k+c+d)=810。a+b+c+d=270,即这个年级共有270人,故应选B。
26、甲、乙二人2小时共加工54个零件,甲加工3小时的零件比乙加工4小时的零件还多4个。甲每小时加工多少个零件?_____
A: 11B: 16C: 22D: 32
参考答案: B 本题解释: 【解析】B。解法一、设俩人速度分别为x、y,则2x+2y=54,3x-4y=4,解得x=16;解法二、从第一句话知D不对。从第二句话中知甲每小时加工的零件是4的倍数。
27、在一个口袋中有l0个黑球、6个白球、4个红球.至少从中取出多少个球才能保证其中有白球? _____
A: 14B: 15C: 17D: 18
参考答案: B 本题解释:【答案】B.解析:抽屉原理,最坏的情况是10个黑球和4个白球都拿出来了,最后第15次拿到的肯定是白球。
28、有5位田径运动员争夺3项比赛的冠军,若每项只设1名冠军,则获得冠军的情况可能有_____。
A: 124种B: 125种C: 130种D: 243种
参考答案: B 本题解释: B [解析] 每项比赛的冠军都有5种可能性,所以获得冠军的情况有C15×C15×C15=125(种)。故本题选B。
29、一项任务甲做要半小时完成,乙做要45 分钟完成,两人合作需要多少分钟完成?_____
A: 12B: 15C: 18D: 20
参考答案: C 本题解释:【解析】直接设90的总量,两人每分钟分别是3和2。所以90/(3+2)=18。
30、一根木杆,第一次截去了全长的1/2,第二次截去所剩木杆的1/3,第三次截去所剩木杆的1/4,第四次截去所剩木杆的1/5,这时量得所剩木杆长为6厘米。问:木杆原来的长是多少厘米?_____
A: 15B: 26C: 30D: 60
参考答案: C 本题解释: C解析: 6÷(1-1/5)÷(1-1/4)÷(1-1/3)÷(1-1/2)6÷(4/5×3/4×2/3×1/2)6÷1/5=30(厘米)故本题选C。
31、在下图中,大圆的半径是8。求阴影部分的面积是多少_____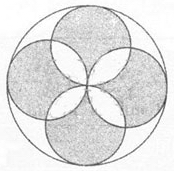
A: 120B: 128C: 136D: 144
参考答案: B 本题解释:【答案】B。解析:割补法。阴影部分可拼成一条对角线长为16的正方形。如图,故面积是16×16÷2=128。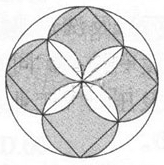
32、2 年前甲年龄是乙年龄的2 倍,5 年前乙年龄是丙年龄的1/3,丙今年11 岁,问甲今年几岁?_____
A: 12B: 10C: 9D: 8
参考答案: A 本题解释: 【解析】五年前乙是(11-5)/3=2岁,所以今年是7岁,两年前是5岁。所以2年前甲是10岁,今年是12岁,选A。
33、有一只怪钟,每昼夜设计成10小时,每小时100分钟,当这只怪钟显示5点时,实际上是中午12点。当这只怪钟显示8点50分时,实际上是什么时间? _____
A: 17点50分B: 18点10分C: 20点O4分D: 20点24分
参考答案: D 本题解释:D。怪钟时间从5点走到8点50分的3个小时50分来源:91考试 网钟,相当于标准时间一天的35%,即24×0.35=8.4小时。因此实际时间为12+8.4=20.4时,即20点24分。
34、小张、小王二人同时从甲地出发,驾车匀速在甲乙两地之间往返行驶。小张的车速比小王快,两人出发后第一次和第二次相遇都在同一地点,那么小张的车速是小王的_____倍。
A: 1.5B: 2C: 2.5D: 3
参考答案: B 本题解释:【解析】B。行程问题。采用比例法。由题意,两人从同地出发,则第一次相遇时两人的路程和为2个全程,设其中小张走了x,小王走了y;第二次相遇 时两人走了4个全长,小张走了2y,小王走了x-y;由比例法x÷y=2y÷(x-y),解得x=2y,故两人速度比为2:1。
35、甲、乙、丙、丁四个人比赛打羽毛球,每两个都要赛一场,已知甲胜了丁,并且甲、乙、丙三人胜的场数相同,那么丁胜了几场?_____
A: 6 B: 0 C: 12 D: 3
参考答案: B 本题解释:【解析】B。每人至多赛3场,排除A、C。甲胜丁,则丁至少输1场,排除D。
36、100张多米诺骨牌整齐地排成一列,依顺序编号为1、2、3……99,100.第一次拿走所有奇数位置上的骨牌,第二次再从剩余骨牌中拿走所有奇数位置上的骨牌,依此类推。请问最后剩下的一张骨牌的编号是多少?_____
A: 32B: 64C: 88D: 96
参考答案: B 本题解释:B。【解析】本题关键是理解题意,第一次拿走的是所有奇数,第二次拿走的各项是2分别乘以1、3、5、7、9……,依次类推,每拿走一次后,剩下的第一个数是20、21,22、23、24……,在100之内要使2n取值最大,所以最后剩下的是64,选B。
37、某单位今年新进了3 个工作人员,可以分配到3 个部门,但每个部门至多只能接收2 个人,问:共有几种不同的分配方案?_____
A: 12 B: 16 C: 24 D: 以上都不对
参考答案: C 本题解释:【答案】C[解析]每部门都有三种选择,再减去3人同一部门的情况,所以3的3次方-3=24,选C。
38、小张和小王同时骑摩托车从A地向B地出发,小张的车速是每小时40公里,小王的车速是每小时48公里。小王到达B地后立即向回返,又骑了15分钟后与小张相遇。那么A地与B地之间的距离是多少公里?_____
A: 144B: 136C: 132D: 128
参考答案: C 本题解释:C。
39、某数的百分之一等于0.003,那么该数的10倍是多少?_____。
A: 0.003B: 0.03C: 0.3D: 3
参考答案: D 本题解释:D【解析】某数的百分之一为0.003,则该数为0.3,那么它的10倍为3。故正确答案为D。
40、甲、乙沿同一公路相向而行,甲的速度是乙的1.5倍,已知甲上午8点经过邮局,乙上午10点经过邮局。问:甲乙在中途何时相遇?_____
A: 8点48分 B: 8点30分 C: 9点 D: 9点10分
参考答案: A 本题解释:A。【解析】设乙的速度为x,甲就是1.5x,当甲8点到邮局时,乙离邮局还有2个小时的路程(2x),甲乙走完2x路程需要2x/(1.5x+x)=4/5小时=48分钟,加上8点,就是8点48分相遇。
41、小明和小强从400米环形跑道的同一点出发,背向而行。当他们第一次相遇时,小明转身往回跑;再次相遇时,小强转身往回跑;以后的每次相遇分别是小明和小强两人交替调转方向。小明每秒跑3米,小强每秒跑5米,则在两人第30次相遇时。小明共跑了多少米? _____
A: 11250B: 13550C: 10050D: 12220
参考答案: A 本题解释:A。两人相向运动,经过400÷(3+5)=50秒相遇,之后小明转身,两人做追及运动,经过400÷(5-2)=200秒第二次相遇;接着两人又做相向运动,经过50秒相遇,再做追及运动,经过200秒相遇,以此类推,第30次相遇共用30÷2×(50+200)=3750秒,则小明共跑了3×3750=11250米。
42、前馈控制是指通过观察情况、收集整理信息、掌握规律、预测趋势,正确预计未来可能出现的问题,提前采取措施,将可能发生的偏差消除在萌芽状态中,避免在未来不同发展阶段可能出现的问题而事先采取的措施。根据上述定义,下列不属于前馈控制的是_____。
A: 人力资源部的马经理了解各部门的人员缺口、岗位要求等信息后,决定本轮招聘的职位和数量B: 某厂进了一批原料,经理要求质检人员对其进行抽样检查,避免不合格原料流人车间C: 某宾馆经理接到客人投诉客房空调不能使用后,立刻为客人调换了房间,并且组织人员对所有客房的空调进行了检查D: 某公司将制造环节外包给外地一家工厂,并在建设生产线的同时,培训对方的技术人员和质检人员
参考答案: C 本题解释:定义的关键在于“预计未来可能出现的问题”,“提前采取措施”。A项,马经理了解各部门的人员缺口、岗位要求等信息,属于收集整理信息,而他决定本轮招聘的职位和数量,属于对未来的预测,是为了避免未来出现人员紧缺或不符合岗位要求的问题,故属于前馈控制。B项,质检人员进行抽样检查,属于收集信息,目的是避免不合格原料流入车间,属于提前采取措施,是前馈控制。D项,某公司在工厂开工之前就培训技术人员和质检人员,也属于“提前采取措施”,符合定义。C项,客人投诉空调不能使用,这是已经发生的问题,而不是“未来可能出现的问题”,故不符合定义。本题选C。
43、有人将1/10表示为1月10日,也有人将1/10表示为10月1日,这样一年中就有不少混淆不清的日期了,当然,8/15只能表示8月15日,那么,一年中像这样不会搞错的日期最多会有多少天?_____
A: 221B: 234C: 216D: 144
参考答案: B 本题解释:【答案】B。解析:当日期在1-12中取值时才会混淆,其中在1月1日,2月2日,......12月12日不会混淆。共有12×12-12=132天会混淆,若是平年,则一年中不会混淆的日期会有365-132=233天,若是闰年则多一天,所以最多会有234天。
44、7,77,777,7777……,如果把前77个数相加,那么它们的和的末三位数是多少?_____。
A: 359B: 349C: 329D: 379
参考答案: A 本题解释:【答案】A。解析:把每一个数的末三位相加即可,也即7+77+777×75=58359。
45、将10克盐和200克浓度为5%的盐水一起加入一杯水中,可得浓度为2.5%的盐水,则原来杯中水的克数是_____。
A: 570B: 580C: 590D: 600
参考答案: C 本题解释:C。
46、杂货店分三次进了一些货物,已知每一次的进货单价都是上一次的80%,且第一次的进货单价为5元。已知这些货物恰好能够排成一个三层的空心方阵,且最内层、中间层和最外层恰好分别是第一、二、三次所进的货物,且最外层每边有7个货物。现要保证20%利润率的情况下,杂货店应该将货物至少定为多少元?_____
A: 3.90B: 4.12C: 4.36D: 4.52
参考答案: D 本题解释:【解析】D。三次的单价分别为5元、5×80%=4元、4×80%=3.2元。最外层有货物(7-1)x4=24个,中间层有24-8=16个,最内层有I6-8=8个。所以总进价为3.2x24+4xl6+5x8=l80.8元,要保证20%的利润率,货物定价为180.8x(1+20%)÷(24+16+8)=4.52元。
47、有甲、乙两项工程,张师傅单独完成甲工程需6天,单独完成乙工程需30天,李师傅单独完成甲工程需18天,单独完成乙工程需24天,若合作两项工程,最少需要的天数为:_____
A: 16天B: 15天C: 12天D: 10天
参考答案: A 本题解释:【答案】A。中解析:分析题意可知,张师傅作甲工程的效率较高,李师傅做乙工程的效率较高,因此李师傅做乙工程,张师傅先用6天完成甲工程,之后与李师傅异同完成乙工程,这样所需的天数最少。
48、四人进行篮球传接球练习,要求每人接到球后再传给别人,开始由甲发球,并作为第一次传球。若第五次传球后,球又回到甲手中,则共有传球方式多少种:_____
A: 60;B: 65;C: 70;D: 75;
参考答案: A 本题解释:【答案解析】:选A,球第一次与第五次传到甲手中的传法有:C(1,3)×C(1,2)×C(1,2)×C(1,2)×C(1,1)=3×2×2×2×1=24,球第二次与第五次传到甲手中的传法有:C(1,3)×C(1,1)×C(1,3)×C(1,2)×C(1,1)=3×1×3×2×1=18,球第三次与第五次传到甲手中的传法有:C(1,3)×C(1,2)×C(1,1)×C(1,3)×C(1,1)=3×2×1×3×1=18,24+18+18=60种,具体而言:分三步:(1)在传球的过程中,甲没接到球,到第五次才回到甲手中,那有3×2×2×2=24种,第一次传球,甲可以传给其他3个人,第二次传球,不能传给自己,甲也没接到球,那就是只能传给其他2个人,同理,第三次传球和第四次也一样,有乘法原理得一共是3×2×2×2=24种。(2)因为有甲发球的,所以所以接下来考虑只能是第二次或第三次才有可能回到甲手中,并且第五次球才又回到甲手中。当第二次回到甲手中,而第五次又回到甲手中,故第四次是不能到甲的,只能分给其他2个人,同理可得3×1×3×2=18种。(3)同理,当第三次球回到甲手中,同理可得3×3×1×2=18种。最后可得24+18+18=60种
49、现有一个无限容积的空杯子,先加入1克酒精,再加入2克水,再加入3克酒精,再加入4克水,……,如此下去,问最终杯子中酒精溶液浓度为多少?_____ B: 25%C: 33.3%D: 50%
参考答案: D 本题解释:【解析】D。如果把加一次酒精和水看成一个流程,则经过n个流程后,杯子里面有1+3+5+…+(2n-1)=1/2n(1+2n-1)=n2克酒精,而酒精溶液有1+2+…+2n=1/2×2n(1+2n)=n(1+2n)克。故此时酒精溶液浓度为n2/n(1+2n)=n/(2n+1),当n趋于无穷大时,溶液浓度趋于1/2=50%。思路点拨:极端法,当加入酒精或水的量极大时连续两次操作水与酒精的差距对整体的影响可以忽略不计,因此必然各占50%。
50、两排蜂房,一只蜜蜂从左下角的1号蜂房到8号蜂房,假设只向右方(正右或右上或右下)爬行,则不同的走法有_____。
A: 16种B: 18种C: 21种D: 24种
参考答案: C 本题解释: 
51、某校人数是一个三位数,平均每个班级36人,若将全校人数的百位数与十位数对调,则全校人数比实际少180人,那么原校人数最多可以达到多少人:_____
A: 900B: 936 C: 972D: 990
参考答案: C 本题解释:C。【解析】根据能被36整除和百位十位对调后相差180两个条件,用代入法可很快求得。
52、某项工程计划300天完成,开工100天后,由于施工人员减少,工作效率下降20%,问完成该工程比原计划推迟多少天? _____
A: 40B: 50C: 60D: 70
参考答案: B 本题解释: B。根据效率与时间成反比,可得正常200天的工作,效率下降后需要200÷ (1-20%) =250天,故需推迟50天。
53、一客轮从沙市顺流而下开往武汉需要2天,从武汉逆水而上开往沙市需要3天。一木筏从沙市顺流需要_____天到达武汉。
A: 8B: 12C: 15D: 22
参考答案: B 本题解释:B[解析]设水流速度为每天x个长度单位,客轮在静水中的速度为每天y个长度单位,列方程得(y+x)×2=(y-x)×3y=5x沙市到武汉的水路长:(5x+x)×2=12x(个单位);木筏从沙市顺流而下到武汉所需天数为:12x÷x=12(天)。故本题正确答案为B。
54、船在流速为每小时1000米左右的河上逆流而上,行至中午12点时,有一乘客的帽子落到了河里。乘客请求船家返回追赶帽子,这时船已经开到离帽子100米远的上游。已知在静水中这只船的船速为每分钟20米。假设不计调头的时间,马上开始追赶帽子,问追回帽子应该是几点几分?_____
A: 12点10分B: 12点15分C: l2点20分D: 12点30分
参考答案: A 本题解释:【解析】A。本题不需要考虑水速。船和帽子的相对速度为每分钟20米,距离相差100米,可得追上帽子需要5分钟;发现帽子到返回追帽子船走了100米,此段路程所花的时间为5分钟,则追回帽子应该是12点10分。
55、1-2+3-4+5-6+7-8+…+1989-1990+1991=_____
A: 895 B: 896 C: 995 D: 996
参考答案: D 本题解释: D。原式可等于1+1990/2=996。故正确答案为D。
56、有一种红砖,长24厘米、宽12厘米、高5厘米,问至少用多少块这种砖才能拼成一个实心的正方体?_____
A: 600块B: 1200块C: 1800块D: 2400块
参考答案: B 本题解释:B。
57、有100人参加运动会的三个比赛项目,每人至少参加一项,其中未参加跳远的有50人,未参加跳高的有60人,未参加赛跑的有70人。问至少有多少人参加了不止一个项目?_____
A: 7B: 10C: 15D: 20
参考答案: B 本题解释:B【解析】最值问题。由题意,参加跳远的人数为50人,参加跳高的为40人,参加赛跑的为30人;即参加项目的人次为120人次;故欲使参加不止一项的人数最少,则需要使只参加一项的人数最多为x,参加3项的人数为y;故x+3y=120,x+y=100,解得y=10。
58、有6张卡片,分别写着数字1,2,5,6,8,9。现在从中取出3张卡片,并排放在一起,组成一个三位数。问可以组成多少个不同的偶数?_____
A: 144个B: 120个C: 60个D: 12个
参考答案: C 本题解释: 
59、篮球规则中得分有3分,2分,1分,若在一次比赛中,队员A一人得了13分,那么他的得分组合共_____种。
A: 18 B: 19 C: 20 D: 21
参考答案: D 本题解释:D[解析]当A的3分分别拿到4,3,2,1,0次的时候,对应的组合数分别是1,3,4,6,7,所以A的得分组合共有1+3+4+6+7=21种,选D。
60、100人参加7项活动,已知每个人只参加一项活动,而且每项活动参加的人数都不一样,那么,参加人数第四多的活动最多有几个人参加?_____
A: 22B: 21C: 24D: 23
参考答案: A 本题解释:总的人数是固定的100人,要使参加人数第四多的活动最多,且每项的人数不一样,则其他的项的人数要尽量的少,那么,最后三名人数最少分别为1,2,3。设第四名的人数为x人,则前三名最少分别为(x+1),(x+2),(x+3),那么:1+2+3+x+(x+1)+(x+2)+(x+3)=100,解得x=22,故参加人数第四多的活动最多有22人参加。故选A。
61、一本100多页的书,被人撕掉了4张.剩下的页码总和为8037。则该书最多有多少页_____
A: 134B: 136C: 138D: 140
参考答案: A 本题解释:【答案】A。解析:撕掉四张纸的页码数之和是偶数,由剩下页码数是奇数可知总的页码数是奇数,排除B、D。若为C,则撕掉的页码数之和是138×(138+1)÷2—8037=1554>138×8,矛盾。A项符合题意。
62、一间长250米、宽10米、高4米的仓库放置了1000个棱长为1米的正方体箱子,剩余的空间为多少立方米_____
A: 0B: 1500C: 5000D: 9000
参考答案: D 本题解释: 【解析】D。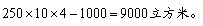
63、甲乙丙丁四个数的和为43,甲数的2倍加8,乙数的3倍,丙数的4倍,丁数的5倍减去4,都相等,问这四个各是多少?_____
A: 14 12 8 9B: 16 12 9 6C: 11 10 8 14 D: 14 12 9 8
参考答案: D 本题解释:D。【解析】根据4个数的和为43、前三个数的关系,用带入法很容易得到答案。解:设得到的四个数为x,得(x-8)÷2+x÷3+x÷4+(x+4)÷5=43,解得:x=36,甲:(36-8)÷2=14,乙:36÷3=12,丙:36÷4=9,丁:(36+4)÷5=8.答:甲为14,乙为12,丙为9,丁为8.
64、南阳中学有语文教师8名、数学教师7名、英语教师5名和体育教师2名。现要从以上四科教师中各选出1名教师去参加培训,问共有几种不同的选法_____
A: 96种 B: 124种 C: 382种 D: 560种
参考答案: D 本题解释:【解析】D。根据乘法原理,各选1名的选法共有8×7×5×2=560(种)。
65、某商店将定价为6.25元的笔记本降价20%卖出,结果还获成本25%的利润。笔记本的成本为_____。
A: 5元B: 4元C: 3元D: 2元
参考答案: B 本题解释:B【解析】设成本为x元,计算得x=4。
66、比-5大-7的数是_____。
A: -3B: 2C: -12D: -7
参考答案: C 本题解释: C [解析] -5+(-7)=-12。故本题选C。
67、某公司要到外地去推销产品,产品成本为每件3000元。从公司到外地距离是400千米,运费为每件产品每运1千米收1.5元。如果在运输及销售过程中产品的损耗是10%,那么公司要想实现25%的利润率,零售价应是每件多少元? _____
A: 4800B: 5000C: 5600D: 6000
参考答案: B 本题解释:【答案】B。解析:以1件商品为例,成本为3000元,运费为1.5×400=600元,则成本为3000+600=3600元,要想实现25%的利润率,应收入3600×(1+25%)=4500元;由于损耗,实际的销售产品数量为1×(1-10%)=90%,所以实际零售价为每件4500÷90%=5000元。
68、某次投资活动在三个箱子中均放有红、黄、绿、蓝、紫、橙、白、黑8种颜色的球各一个,奖励规则如下:从三个箱子中分别摸出一个球,摸出的3个球均 为红球的得一等奖,摸出的3个球中至少有一个绿球的得二等奖,摸出的3个球均为彩色球(黑.白除外)的得三等奖。那么不中奖的概念是_____。
A: 在0-25%之间B: 在25-50%之间C: 在50-75%之间 D: 在75-100%之间
参考答案: C 本题解释:【解析】C。概率问题。中奖概率为(3/4)3+C13×(1/8)×(1/4)2+C23×(1/8)2×(1/4)=117÷256<50%,故不中奖的概率略大于50%。
69、一个长方体的长、宽、高恰好是三个连续的自然数,并且它的体积数值等于它的所有棱长之和的2倍,那么这个长方体的表面积是_____
A: 74B: 148C: 150D: 154
参考答案: B 本题解释:【解析】B。设该长方体的长、宽、高分别是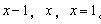 。那么有
。那么有 所以这个长方体的表面积为
所以这个长方体的表面积为
70、(101+103+…+199)-(90+92+…+188)=_____。
A: 100 B: 199 C: 550 D: 990
参考答案: C 本题解释:C[解析]提取公因式法。101-90=11,103-92=11,……,199-188=11,总计有50个这样的算式,所以50×11=550,选择C。
71、李先生去10层楼的8层去办事,恰赶上电梯停电,他只能步行爬楼。他从第1层爬到第4层用了48秒,请问,以同样的速度爬到第8层需要多少秒? _____
A: 112B: 96C: 64D: 48
参考答案: A 本题解释:A【解析】假设每上一层楼的路程为一段楼梯,李先生从第1 层爬到第4 层,路程为3 段楼梯,用时48 秒,则每一段楼梯用时16 秒,第1 层到第8 层路程为7 段,则需用时16×7=112 秒。故选A。
72、有一笔奖金,按1:2:3的比例来分,已知第三人分450元,那么这笔奖金总共是_____元。
A: 1150 B: 1000 C: 900 D: 750
参考答案: C 本题解释:C。根据题意可知,这笔奖金共分为6份,而分到3份的第三人拿到了450元,则6份当是450×2=900元。所以正确答案为C项。
73、18名游泳运动员,有8名参加仰泳,有10名参加蛙泳,有12名参加自由泳,有4名既参加仰泳又参加蛙泳,有6名既参加蛙泳又参加自由泳,有5名既参加仰泳又参加自由泳,有2名这3个项目都参加。这18名游泳运动员中,只参加1个项目的有多少名?_____
A: 5B: 6C: 7D: 4
参考答案: B 本题解释: 【解析】B。利用文氏图可以迅速准确地求得答案。注意本题目的陷阱,18名运动员并不是都参加了项目。 由图可知;只参加一个项目的有l+2=3=6名。
由图可知;只参加一个项目的有l+2=3=6名。
74、一根木杆,第一次截去了全长的1/2,第二次截去所剩木杆的1/3,第三次截去所剩木杆的1/4,第四次截去所剩木杆的1/5,这时量得所剩木杆长为6厘米。问:木杆原来的长是多少厘米?_____
A: 15B: 26C: 30D: 60
参考答案: C 本题解释:【解析】:6÷(1-1/5)÷(1-1/4)÷(1-1/3)÷(1-1/2)=6÷(4/5×3/4×2/3×1/2)=6÷1/5=30(厘米)故本题选C。
75、一个工人加工一批产品,他每加工出一件正品,得报酬0.75元,每加工出一件次品,罚款1.50元。这天他加工的正品是次品的7倍,得款11.25元。那么他这天加工出多少件次品?_____
A: 1B: 3C: 7D: 13
参考答案: B 本题解释:B【解析】 工人加工7件正品得款0.75×7=5.25(元),加工出一件次品罚款1.50元,所以每加工8件产品得款5.25-1.50=3.75(元)。所以他这天加工出的次品是11.25÷3.75=3(件)。
76、混合并购是指一个企业对那些与自己生产的产品不同性质和种类的企业进行并购的行为,其中目标公司与并购企业既不是同一行业,又没有纵向关系。根据上述定义,下列属于混合并购的是_____。
A: 某碳酸饮料公司收购了一家灌装公司和一家饼干公司B: 某网站收购了一家户外传媒公司和一家网络游戏公司C: 某出版集团收购了一家印刷厂和一家文学网站D: 某电脑集团收购了一家酒厂和一家葡萄庄园
参考答案: D 本题解释:定义的关键信息是“目标公司与并购企业既不是同一行业,又没有纵向关系”。A项,灌装公司可以为饮料提供包装,因此和并购企业存在纵向关系,而饼干公司则和碳酸饮料公司都属于食品行业。B项,网站属于互联网传媒,因此网站和户外传媒属于同一行业;同时,网站也可能提供网络游戏,因此网站与网络游戏公司也可能存在纵向关系。C项,印刷是出版的一道流程,因此印刷厂和出版集团存在纵向关系。D项,酒厂和葡萄庄园虽然有可能存在纵向关系,但是二者与并购企业——电脑集团的产品性质完全不同,且不存在任何关系,因此选D。
77、423×187-423×24-423×63的值是_____。
A: 41877B: 42300C: 42323D: 42703
参考答案: B 本题解释: B 【解析】原式可化为423×(187-24-63)。
78、有甲、乙两只钟表,甲表8时15分时,乙表8时31分。甲表比标准时间每9小时快3分,乙表比标准时间每7小时慢5分。至少要经过几小时,两钟表的指针指在同一时刻?_____
A: 12(7/11)B: 15C: 15(3/11)D: 17(8/11)
参考答案: C 本题解释: C 解析: 甲表比标准时间每小时快3/9=1/3分,乙表比标准时间每小时慢5/7分。甲、乙两表每小时相差是1/3+5/7=22/21分8时31分-8时15分=16分按追及问题,追及路程为16分,速度差是每小时22/21分,求追及时间。16÷22/21=16×21/22=15(3/11)(小时)至少再经过15311小时,两钟表的指针指在同一时刻。
79、分数4/9、17/35、101/203、3/7、151/301中最大的一个是_____。
A: 4/9B: 17/35C: 101/203D: 151/301
参考答案: D 本题解释:D【解析】首先目测可以知道3/7、17/35和101/203都小于1/2,而4/9和151/301都大于1/2,所以只要比较二者的大小就可以,通过计算,151/301大,所以选择D。
80、小雪买了7瓶酸奶,共付款17.5元,喝完全部酸奶退瓶时,知道每个空瓶的价钱比瓶中酸奶的价钱少1.5元,那么小雪应收到退款多少元?_____
A: 5元B: 4.5元C: 3元D: 3.5元
参考答案: D 本题解释:D【解析】设每瓶瓶中酸奶x元,则每个瓶子的押金为(x-1.5)元。则得:7×[x+(x-1.5)]=17.5,解得x=2(元)。所以每个瓶子的押金为2-1.5=0.5元,应退款:7×0.5=3.5元。
81、为了把2008年北京奥运办成绿色奥运,全国各地都在加强环保,植树造林。某单位计划在通往两个比赛场馆的两条路的(不相交)两旁栽上树,现运回一批树苗,已知一条路的长度是另一条路长度的两倍还多6000米,若每隔4米栽一棵,则少2754棵;若每隔5米栽一棵,则多396棵,则共有树苗_____。
A: 8500棵B: 12500棵C: 12596棵D: 13000棵
参考答案: D 本题解释:答案:D。设两条路共长z米,共有树苗y棵,在两条路的两旁栽树则有4条线要栽树。则x÷4+4=y+2754,x÷5+4=y-396,解出y=13000棵,所以选D。
82、某市出租车收费标准是:5千米内起步费10.8元,以后每增加1千米增收1.2元,不足1千米按1千米计费。现老方乘出租车从A地到B地共支出24元,如果从A地到B地先步行460米,然后再乘出租车也是24元,那么从AB的中点C到B地需车费_____元。(不计等候时间所需费用)
A: 12B: 13.2C: 14.4D: 15.6
参考答案: C 本题解释:经济M题。共花钱24元,超过5千米的部分为24-10.8=13.2(元),超过5千米后走了13.2÷1.2=11(千米),总路程最多为16千米,因为步行460米后花费相同,说明460米后的路程一定超过15千米,则总路程15+0.46<S≤16,则C到B的距离7.73<< p>S/2≤8,因不足1千米按1千米计费,故应看成8千米,共花费10.8-9(8-5)×1.2=14.40(元)。
83、在一条公路上每隔100公里有一个仓库,共有5个仓库,一号仓库存有10吨货物,二号仓库存有20吨货物,五号仓库存有40吨货物,其余两个仓库是空的。现在要把所有的货物集中存放在一个仓库里,如果每吨货物运输1公里需要0?5元运输费,则最少需要运费_____。
A: 4500元B: 5000元C: 5500元D: 6000元
参考答案: B 本题解释:[解析]正确答案为B。根据题意,一至五号仓库为依次排列,最有效的货物集中方式为把一和二号仓库中的货物集中到五号仓库中,则总费用为0.5×(300×20+400×10)=5000元,所以选择B项。
84、牧场上一片青草,每天牧草都匀速生长。这片牧草可供10头牛吃20天,或者可供15头牛吃10天。问:可供25头牛吃几天?_____
A: 5B: 10C: 15D: 20
参考答案: A 本题解释:A【解析】 这类题难就难在牧场上草的数量每天都在发生变化,我们要想办法从变化当中找到不变的量。总草量可以分为牧场上原有的草和新生长出来的草两部分。牧场上原有的草是不变的,新长出的草虽然在变化,因为是匀速生长,所以这片草地每天新长出的草的数量相同,即每天新长出的草是不变的。下面,就要设法计算出原有的草量和每天新长出的草量这两个不变量。设1头牛一天吃的草为1份。那么,10头牛20天吃200份,草被吃完;15头牛10天吃150份,草也被吃完。前者的总草量是200份,后者的总草量是150份,前者是原有的草加 20天新长出的草,后者是原有的草加10天新长出的草。200-150=50(份),20-10=10(天),说明牧场10天长草50份,1天长草5份。也就是说,5头牛专吃新长出来的草刚好吃完,5头牛以外的牛吃的草就是牧场上原有的草。由此得出,牧场上原有草(l0-5)× 20=100(份)或(15-5)×10=100(份)。现在已经知道原有草100份,每天新长出草5份。当有25头牛时,其中的5头专吃新长出来的草,剩下的20头吃原有的草,吃完需100÷20=5(天)。所以,这片草地可供25头牛吃5天。因此,正确答案为A。
85、商店为某鞋厂代销200双鞋,代销费用为销售总额的8%。全部销售完后,商店向鞋厂交付6808元。这批鞋每双售价为多少元?_____
A: 30.02B: 34.04C: 35.6D: 37
参考答案: D 本题解释: 【解析】D。解法一、设每双售价x元,则200x×(1-8%)=6808;解法二、交付钱数6808元必然能除尽每双售价,依此排除A、C。如果是B,很容易发现200双正好6808元,没有代销费用了。
86、A大学的小李和B大学的小孙分别从自己学校同时出发,不断往返于A、B两校之间。现已知小李的速度为85米/分,小孙的速度为105米/分,且经过12分钟后两人第二次相遇。问A,B两校相距多少米?_____
A: 1140米B: 980米C: 840米D: 760米
参考答案: D 本题解释:易知到第二次相遇时,两人合起来走过的距离恰为A、B两校距离的3倍,因此A、B两校相距(85+105)×12÷3=760(米)。故选D。
87、已知两个四位数的差为7930,问这两个四位数的和最大值为多少?_____
A: 12068B: 12560C: 13268D: 13650
参考答案: A 本题解释:A。要使两数的和尽量的大,则应使这两个数尽量大,取较大的数为9999,则较小的为9999-7930=2069,它们的和等于9999+2069=12068,选A。
88、某单位有185人。在某次乒乓球比赛中。有12%的男员工和12.5%的女员工参加这次比赛。则该单位男员工有多少人?_____
A: 25B: 65C: 105D: 125
参考答案: A 本题解释:A。
89、某商品按定价的80%(八折)出售,仍能获得20%的利润,问定价时期望的利润率是多少?_____
A: 50%B: 40%C: 30%D: 20%
参考答案: A 本题解释:【答案解析】设成本为1,根据定价的80%=1.2,所以定价为1.5,1.5-1=0.5,选A。考查对于利润的理解:单个商品利润=售价-成本,获得百分之几的利润是相对于成本来说的,如我们生产一支笔成本1元,我们将它以1.5元出售,则获得利润为0.5元,因为(0.5/1)*100%=50%,所以获得了50%的利润解法如下:设定价为y,成本为x,则按定价80%出售,仍获得20%利润用数学公式表示就是0.8y-x=0.2x,即售价-成本=利润因此,得y=3x/2,或按原价出售,则利润为,y-x=3x/2-x=x/2即利润率为50%。
90、某医院有一氧气罐匀速漏气,该氧气罐充满后同时供40人吸氧,60分钟后氧气耗尽,再次充满该氧气罐同时供60个人吸氧,则45分钟后氧气耗尽。问如果该氧气罐充满后无人吸氧,氧气耗尽需要多长时间?_____
A: 1.5小时B: 2小时C: 2.5小时D: 3小时
参考答案: D 本题解释:【答案】D。解析:这是一个变形的牛吃草问题。设原有氧气为M,漏气速度为V,则可得(40+V)×60=(60+V)×45=M,解得V=20,M=3600,如果没人吸氧,则可得耗尽的时间为3600÷20=180分钟,即3小时。故正确答案为D。
91、光的速度是每秒30万千米,太阳离地球1亿5千万千米。问:光从太阳到地球要用几分钟?_____
A: 83B: 12C: 7.2D: 20
参考答案: A 本题解释:【答案】A。解析:150000000÷300000÷60=150÷3÷6=50÷6=8.3(分)。故应选择A。
92、四人进行篮球传接球练习,要求每人接球后再传给别人。开始由甲发球,并作为第一次传球,若第五次传球后,球又回到甲手中,则共有传球方式_____。
A: 60种B: 65种C: 70种D: 75种
参考答案: A 本题解释:[解析]正确答案为A。细分一下传球路径,第一次接球的人只能是非甲,第二第三次接球的人可能是甲或非甲,第四次接球的人只能是非甲,第五次接球的人一定是甲,每次传球后接到球的人可分析如下:第一次第二次第三次第四次第五次第一种情况:非甲甲非甲非甲甲第二种情况:非甲非甲甲非甲甲第三种情况:非甲非甲非甲非甲甲按排列组合,第一种情况的传球方式有3×1×3×2×1=18,第二种有3×2×1×3×1=18,第三种情况有3×2×2×2×l=24,相加共有60种,故选A。
93、每条长200米的三个圆形跑道共同相交于A点,张三、李四、王五三个队员从三个跑道的交点A处同时出发,各取一条跑道练习长跑。张三每小时跑5公里,李四每小时跑7公里,王五每小时跑9公里。问三人第四次在A处相遇时,他们跑了多长时间?_____
A: 40分钟B: 48分钟C: 56分钟D: 64分钟
参考答案: B 本题解释:【答案解析】分别求出跑1米所用的时间。60/5000=张三,60/7000=李四,60/9000=王五。张三跑完200米要12/5分钟(2.4),李四需要12/7(1.7)分钟,王五需要4/3(1.3)分钟。张与李圈相差0.7分钟,与王相差1.1分钟,李与王差0.6分钟。得出这样的关系后可以算出张跑到第N圈时(N>4)李和王刚好也在A点,他们2.4分钟时的位移分别为:200m、282m、365m,然后求出圈差的位移82M.165M然后用200分别除以82.165,求出李需要2.44次的2.4分钟就可以再跑200米,王需要1.2次的2.4分钟,然后通分求出共需要多少个2.4分钟就行了。
94、有一工作,甲做2天后乙接着做,做了10天后完成了工作。已知乙单独完成需要30天,那么甲单独完成此工作需要_____天。
A: 3天B: 1天C: 10天D: 2天
参考答案: A 本题解释:【答案解析】由题可知,甲做2天,相当于乙做20天,则乙做30天的工作,甲3天即可完成。
95、某公交线路有15站,假设一辆公交车从起点站出发,从起点站后,每一站都会有到前方每一站下车的乘客各一名上车,那么在第九站和第十站之间,车上有_____人?
A: 48B: 54C: 56D: 60
参考答案: B 本题解释:【答案】B。解析:解析1:总站点数为M,求第N站和第N+1之间车上的人数,有下述公式,车上的人数=N×(M-N),可知所求人数为9×(15-9)=9×6=54,故选B。解析2:第一站点有14个人上车,没有人下车,第二个站点有13个人上,1个人下车,所以到第九站时候,前面上车人数为14,13,12,11,10,9,8,7,6,根据等差数列求和公式,一共有(14+6)×9÷2=90人,下车的人数为1,2,3,4,5,6,7,8,一共有(1+8)×8÷2=36,则到第九站点后,车上人数等于一到第九站上车的人减去一到第九站下车的人数,即90-36=54,故选B选项。此题不用考虑过于复杂,起始站为第一站。
96、一个空的容积为64 升的鼓形圆桶上有A、B 两孔,一种蒸馏水从A 孔流入同 时从B 孔流出,如果通过A 孔的流速为3 升/小时,那么在B 孔的流速为多少升时才能保证用96 小时恰好装满容器?_____
A: 4/3 B: 8/3 C: 7/3 D: 3/7
参考答案: C 本题解释:【答案】C[解析]从A孔流入同时从B孔流出,设流速X,则容器实际蓄水速度为3-X,所以64/(3-X)=96,求出X=7/3。
97、建华中学共有1600名学生,其中喜欢乒乓球的有1180人,喜欢羽毛球的有1360人,喜欢篮球的有1250人,喜欢足球的有1040人,问以上四项球类运动都喜欢的至少有几人?_____
A: 20人B: 30人C: 40人D: 50人
参考答案: B 本题解释:【答案】B。解析:采取逆向思维法。不喜欢乒乓的1600-1180=420,不喜欢羽毛球的1600-1360=240,不喜欢篮球的1600-1250=350,不喜欢足球的1600-1040=560,要使四项运动都喜欢的人数最少,那么不喜欢的人数就要最多那么都尽量不相交,从而达到最多:420+240+350+560=1570人,所以喜欢的最少的为1600-1570=30人,故正确答案为B。
98、两个相同的瓶子装满酒精溶液,一个瓶子中酒精与水的体积比是3:1,另一个瓶子中酒精与水的体积比是4:1,若把两瓶酒精溶液混合,则混合后的酒精和水的体积之比是多少?_____
A: 31:9B: 7:2C: 31:40D: 20:11
参考答案: A 本题解释:【答案解析】(3/4+4/5)/(1/4+1/5)=31:9
99、甲容器有浓度为3%的盐水190克,乙容器中有浓度为9%的盐水若干克,从乙取出210克盐水倒入甲,甲容器中的盐水的浓度是多少? _____
A: 5.45%B: 6.15%C: 7.35%D: 5.95%
参考答案: B 本题解释: B。根据两溶液混合公式可得,3%×190+9%×210=(190+210)×C,解得C=6.15%。故正确答案为B。
100、7个同学排成两排照相,前排3人,后排4人,共有_____种站法。
A: 1680B: 2400C: 2520D: 5040
参考答案: D 本题解释:【解析】相当于把7个元素放在预先指定好的7个不同位置上,因此,是7个同学的全排列,共有P77=5040种站法。