时间:2016-06-23 07:52:23
1、导演从学校选出200名预备群众演员,其中有两人是教师,其余是学生。现在要选出5人上场演出。两名教师都被选的概率有多少?_____
A: 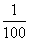 B:
B: 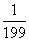 C:
C: 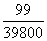 D:
D: 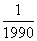
参考答案: D 本题解释:参考答案 题目详解:从200人中选出5人上场:有
题目详解:从200人中选出5人上场:有 种选法;如果2名教师都选出:有
种选法;如果2名教师都选出:有 种选法;所以,两名教师都被选上的概率有
种选法;所以,两名教师都被选上的概率有 ;所以,选D。考查点:数量关系>数学运算>概率问题>单独概率
;所以,选D。考查点:数量关系>数学运算>概率问题>单独概率
2、一个蓄水池有甲、乙、丙三个水管。如果同时打开甲、乙两管,5个小时就能灌满水;如果同时打开乙、丙两管,4个小时就能灌满水。如果先打开乙管6小时,再同时打开甲、丙两管,2小时就能灌满。则单独打开乙管需要几个小时才能灌满水?_____
A: 12B: 15C: 20D: 22
参考答案: C 本题解释:C。
3、有四个数,其中每三个数的和分别是45,46,49,52,那么这四个数中最小的一个数是多少?_____
A: 12B: 18C: 36D: 45
参考答案: A 本题解释:正确答案是A考点平均数问题解析将45、46、49、52直接相加,可知其值等于原来四个数之和的3倍,于是可知原四个数字之和为:(45+46+49+52)÷3=64,因此最小的数为:64-52=12,故选择A选项。秒杀技45为最小的三个数之和,平均数为15,则最小的数必然小于15,仅A符合。
4、(2009江苏)如下图,将一个表面积为36平方米的正方体等分成两个长方体,再将这两个长方体拼成一个大长方体,则大长方体的表面积是_____。 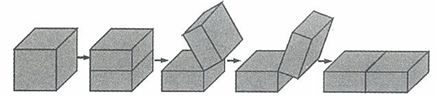
A: 24平方米B: 30平方米C: 36平方米D: 42平方米
参考答案: D 本题解释:参考答案 题目详解:解法一:已知原来正方体每个面的面积都是6平方米,这个过程中,先产生了一个截面,新增了两个平面的面积,即增加了12平方米;原来在右边的那个面在接触过程中被遮住了,不再是表面,即减少了一个平面的面积,即减少了6平方米。综上,大长方体的表面积为
题目详解:解法一:已知原来正方体每个面的面积都是6平方米,这个过程中,先产生了一个截面,新增了两个平面的面积,即增加了12平方米;原来在右边的那个面在接触过程中被遮住了,不再是表面,即减少了一个平面的面积,即减少了6平方米。综上,大长方体的表面积为 平方米。所以,选D。解法二:同样体积的图形当中,越接近于球,表面积越小,所以正方体变成长方体之后,表面积肯定会增加,由此可以直接判断D为正确答案。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
平方米。所以,选D。解法二:同样体积的图形当中,越接近于球,表面积越小,所以正方体变成长方体之后,表面积肯定会增加,由此可以直接判断D为正确答案。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
5、商店卖气枪子弹,每粒1分钱,每5粒4分钱,每10粒7分钱,每20粒1角2分钱。小明的钱至多能买73粒,小刚的钱至多能买87粒,小明和小刚的钱合起来能买多少粒?_____
A: 160B: 165C: 170D: 175
参考答案: B 本题解释:参考答案:B题目详解:小明的钱至多能买73粒:此时小明只能是购买了3个20粒、1个10粒、3个1粒;即小明共有12×3+4+3=46分钱;同理,小刚的钱至多能买87粒:小刚只能是购买了4个20粒,1个5粒,2个1粒;小刚共有12×4+4+2=54分钱,则两人共有100分钱。把100进行数字的拆分:100=12×8+4故此时最多可以买8个20粒,1个5粒,即共买165粒。所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
6、(2009黑龙江)某项工作,甲单独做要18小时完成,乙要24小时完成,丙要30小时才能完成。现按甲、乙、丙的顺序轮班做,每人工作一小时后换班。问当该项工作完成时,乙共做了多长时间?_____
A: 7小时44分B: 7小时58分C: 8小时D: 9小时10分
参考答案: A 本题解释:参考答案:A题目详解:解法一:根据题意,设工作总量为1,则:甲每小时完成: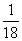 ,乙每小时完成:
,乙每小时完成: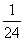 ,丙每小时完成:
,丙每小时完成: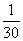 ,所以三个人各工作一小时可完成:
,所以三个人各工作一小时可完成: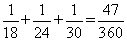 。
。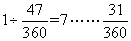 ,所以三人各工作7小时后,还剩下
,所以三人各工作7小时后,还剩下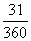 没有完成,由于
没有完成,由于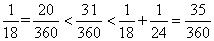 ,所以乙工作的时间为:
,所以乙工作的时间为: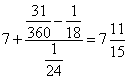 小时,即为7小时44分钟。因此,选A。解法二:18、24、30的最小公倍数是360,根据题意,有:甲、乙、丙三人各工作一小时可完成:
小时,即为7小时44分钟。因此,选A。解法二:18、24、30的最小公倍数是360,根据题意,有:甲、乙、丙三人各工作一小时可完成: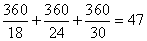
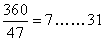 甲再工作一小时还剩:
甲再工作一小时还剩: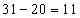
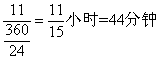 所以乙的工作时间为:7小时44分钟考查点:数量关系>数学运算>工程问题>合作完工问题
所以乙的工作时间为:7小时44分钟考查点:数量关系>数学运算>工程问题>合作完工问题
7、3种动物赛跑,已知狐狸的速度是兔子的 ,兔子的速度是松鼠的2倍,一分钟松鼠比狐狸少跑14米,那么半分钟兔子比狐狸多跑_____米。
A: 28B: 19C: 14D: 7
参考答案: C 本题解释:C【解析】由题意可得:兔子速度∶松鼠速度∶狐狸速度=6∶3∶4,又因为“一分钟松鼠比狐狸少跑14米”即半分钟松鼠比狐狸少跑7米,所以令半分钟兔子、松鼠、狐狸分别跑6a、3a、4a,4a-3a=7,故a=7,所以半分钟兔子比狐狸多跑6×7-4×7=14(米)。
8、有甲、乙两只钟表,甲表8时15分时,乙表8时31分。甲表比标准时间每9小时快3分,乙表比标准时间每7小时慢5分。至少要经过几小时,两钟表的指针指在同一时刻?_____
A: 12(7/11)B: 15C: 15(3/11)D: 17(8/11)
参考答案: C 本题解释: C 解析: 甲表比标准时间每小时快3/9=1/3分,乙表比标准时间每小时慢5/7分。甲、乙两表每小时相差是1/3+5/7=22/21分8时31分-8时15分=16分按追及问题,追及路程为16分,速度差是每小时22/21分,求追及时间。16÷22/21=16×21/22=15(3/11)(小时)至少再经过15311小时,两钟表的指针指在同一时刻。
9、新上任的库房管理员拿着20把钥匙去开20个库房的门,他只知道每把钥匙只能打开其中的一扇门,但不知道哪一把钥匙开哪一扇门,现在要打开所有关闭的20个库房门,他最多要开多少次?_____
A: 80B: 160C: 200D: 210
参考答案: D 本题解释:D【解析】本题应从最不利情况去考虑:打开第一个房间要20次,打开第二个房间要19次……共计要开20+19+18+…+1=210(次)。
10、某单位有员工540人,如果男员工增加30人就是女员工人数的2倍,那么原来男员工比女员工多几人?_____
A: 13B: 31C: 160D: 27
参考答案: C 本题解释:【答案】C。解析:男员工增加30人后,总员工为570人,男员工是女员工的2倍,得女员工为570÷3=190,则原有男员工540-190=350,男员工比女员工多350-190=160人。故正确答案为C。老师点睛:男员工增加30人后,总员工为570人,男员工是女员工的2倍,由于540、30均为偶数,则原有男、女员工的数目也为偶数,男员工比女员工多的人数也是偶数。只有选项C符合条件,故正确答案为C。
11、小张、小王二人同时从甲地出发,驾车匀速在甲乙两地之间往返行驶。小张的车速比小王快,两人出发后第一次和第二次相遇都在同一地点,那么小张的车速是小王的_____倍。
A: 1.5B: 2C: 2.5D: 3
参考答案: B 本题解释:正确答案是B考点行程问题解析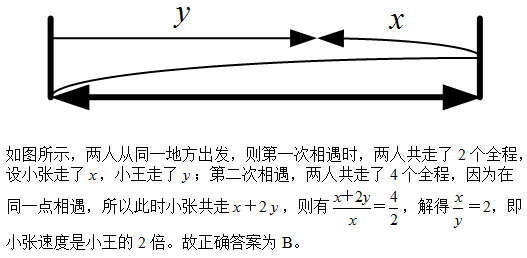
12、一批布料,全部用来做上衣可做60件,全部用来做裤子可做40条,现在做上衣、裤子、裙子各5件,恰好用去全部布料的1/4,剩下布料全部做裙子,则还可以做多少条?_____
A: 80B: 90C: 100D: 110
参考答案: B 本题解释:B【解析】设布料总量为120单位,则每件上衣需2单位布料,每条裤子需3单位布料,又上衣、裤子、裙子各做5件,用去︰120×1/4=30单位,所以每条裙子需1单位布料,则可再生产裙子︰(l20-30)÷1=90(条),故答案为B选项。
13、甲、乙沿同一公路相向而行,甲的速度是乙的1.5倍,已知甲上午8点经过邮局,乙上午10点经过邮局。问:甲乙在中途何时相遇? _____
A: 8点48分B: 8点30分C: 9点D: 9点10分
参考答案: A 本题解释:A。【解析】设乙的速度为x,甲就是1.5x,当甲8点到邮局时,乙离邮局还有2个小时的路程(2x),甲乙走完2x路程需要2x/(1.5x+x)=4/5小时=48分钟,加上8点,就是8点48分相遇。
14、旅客携带了30公斤行李从A地乘飞机去B地,按民航规定,旅客最多可免费携带20公斤行李,超重部分每公斤按飞机票价格的1.5%购买行李票,现该旅客购买了120元的行李票,则他的飞机票价格应是多少?_____
A: 10000 B: 800 C: 600 D: 400
参考答案: B 本题解释:【解析】B。行李超重部分每千克收取120÷(30-20)=12元,则飞机票价为12÷1.5%=800元。
15、去某地旅游,旅行社推荐了以下两个报价方案:甲方案成人每人1000元,小孩每人600元;乙方案无论大人小孩,每人均为700元。现有N人组团,已知1个大人至少带3个小孩出门旅游,那么对于这些人来说_____。
A: 只要选择甲方案都不会吃亏B: 甲方案总是比乙方案更优惠C: 乙方案总是比甲方案更优惠D: 甲方案和乙方案一样优惠
参考答案: A 本题解释:正确答案是A考点统筹规划问题解析因为甲方案中小孩的价格要便宜,因此对甲方案来说1个大人带的小孩越多越划算。考虑题目给出的临界状态,1个大人带3个小孩时平均每个人的价钱恰为700元。因此可知选择甲方案总不会吃亏。故正确答案为A。标签构造调整
16、如果当“张三被录取的概率是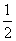 ,李四被录取的概率是
,李四被录取的概率是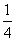 时,命题:要么张三被录取,要么李四被录取”的概率就是_____
时,命题:要么张三被录取,要么李四被录取”的概率就是_____
A: 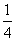 B:
B: 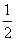 C:
C: 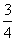 D:
D: 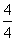
参考答案: B 本题解释:参考答案:B题目详解:“要么张三录取要么李四录取”就是:2人不能同时录取且至少有一人录取;张三被录取的概率是 ,李四被录取的概率是
,李四被录取的概率是 ;那么有两种情况:张三被录取但李四没被录取的概率:
;那么有两种情况:张三被录取但李四没被录取的概率: ;张三没被录取但李四被录取的概率:
;张三没被录取但李四被录取的概率: ;所以,概率为:
;所以,概率为: ;所以,选B。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选B。考查点:数量关系>数学运算>概率问题>条件概率
17、大学的小李和b大学的小孙分别从自己学校同时出发,不断往返于a、b两校之间。现已知小李的速度为85米/分钟,小孙的速度为105米/分钟,且经过12分钟后两人第二次相遇。问a、b两校相距多少米?_____
A: 1140米B: 980米C: 840米D: 760米
参考答案: D 本题解释:正确答案是D考点行程问题解析两人第二次相遇时,两人共走的路程为a、b间距离的3倍,因此a、b两校相距(85+105)×12÷3=190×4=760米。标签尾数法
18、某学校的全体学生刚好排成一个方阵,最外层的人数是108人,则这个学校共有多少学生?_____
A: 724人B: 744人C: 764人D: 784人
参考答案: D 本题解释:正确答案是D考点计数模型问题解析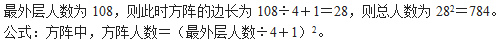 故正确答案为D。秒杀技要拼成方阵,则人数必然为完全平方数,仅D符合。故正确答案为D。
故正确答案为D。秒杀技要拼成方阵,则人数必然为完全平方数,仅D符合。故正确答案为D。
19、1.31×12.5×0.15×16的值是_____。
A: 39.3B: 40.3C: 26.2D: 26.31
参考答案: A 本题解释:答案:A【解析】本式可写为1.31×12.5×4×0.15×4。
20、股票买入和卖出都需要通过证券公司进行交易,每次交易费占交易额的2‰。某人以10元的价格买入1000股股票,几天后又以12元的价格全都卖出,若每次交易还需付占交易额3‰的印花税,则此人将获利_____。
A: 1880元B: 1890元C: 1900元D: 1944元
参考答案: B 本题解释:正确答案是B考点经济利润问题解析交易两次,所以交两次交易费,交两次印花税,故可得如下:(12-10)×1000-(12+10)×1000×(2‰+3‰)=2000-22000×5‰=2000-110=1890,故正确答案为B。
21、现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都做错的有4人,则两种实验都做对的有_____。
A: 27人B: 25人C: 19人D: 10
参考答案: B 本题解释:【答案解析】容斥问题,40+31-X=50-4,所以X=25,选B。
22、某公司的6名员工一起去用餐,他们各自购买了三种不同食品中的一种,且每人只购买了一份。已知盖饭15元一份,水饺7元一份,面条9元一份,他们一共花费了60元。问他们中最多有几人买了水饺?_____
A: 1B: 2C: 3D: 4
参考答案: C 本题解释:正确答案是C考点不定方程问题解析假定购买三种食物人数分别为X、Y、Z,根据题意X+Y+Z=6,15X+7Y+9Z=60。要使得水饺最多,则其他尽可能少。根据奇偶性质,可知X、Y、Z三个数中必然两个为奇数一个为偶数,或者三个均为偶数。将选项代入验证,若Y=4,此时X、Z无正整数解;若Y=3,可知X=2,Z=1,符合题意。因此正确答案为C。秒杀技得到15X+7Y+9Z=60后,注意到15、9、60均能被3整除,因此7Y必然能被3整除,仅C符合。
23、一个四位数与7的和是没有重复数字的最小四位数,问原四位数的个位是多少?_____
A: 3B: 4C: 5D: 6
参考答案: D 本题解释:参考答案 题目详解:首先考虑没有重复数字的最小四位数:没有重复数字组成的最小四位数是1023;原四位数是:
题目详解:首先考虑没有重复数字的最小四位数:没有重复数字组成的最小四位数是1023;原四位数是: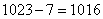 ;所以原四位数的个位是6。所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
;所以原四位数的个位是6。所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
24、甲班有42名学生,乙班有48名学生,在某次数学考试中按百分制评卷,评卷结果两个班的数学总成绩相同,平均成绩都是整数,且都高于80分。请问甲班的平均分与乙班相差多少分?_____
A: 12分B: 14分C: 16分D: 18分
参考答案: A 本题解释:参考答案:A题目详解:根据题意,假设甲乙两班的平均分分别为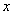 ,
,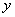 ,(
,(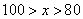 ,
,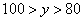
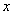 ,
,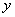 且为整数)。则有:
且为整数)。则有: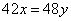 ,即:
,即: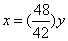 ;由于
;由于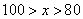 ,且为整数,
,且为整数,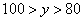 ,且为整数,故:
,且为整数,故: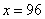 ,
,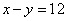 即有:
即有: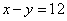 所以,选A(该解析由用户“壁立千仞”于2010-10-2022:02:18贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之算式计算>不定方程问题>二元一次不定方程
所以,选A(该解析由用户“壁立千仞”于2010-10-2022:02:18贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之算式计算>不定方程问题>二元一次不定方程
25、一只船沿河顺水而行的航速为30千米/小时,已知按同样的航速在该河上顺水航行3小时和逆水航行5小时的航程相等,则此船在该河上顺水漂流半小时的航程为_____。
A: 1千米B: 2千米C: 3千米D: 6千米
参考答案: C 本题解释:正确答案是C考点行程问题解析由题意得逆流航行的速度为30×3÷5=18千米/小时,则水速为(30-18)÷2=6千米/小时,顺水漂流半小时的航程为6×0.5=3千米,故正确答案为C。公式:水速=(顺水速度-逆水速度)÷2。标签公式应用
26、除以5余1,b除以5余4,如果3a >b,那么3a-b除以5余几? _____
A: 1B: 2C: 3D: 4
参考答案: D 本题解释:D【解析】3a 除以5 应余1×3=3,已知b 除以5 余4,则3a-b 除以5 余3-4+5=4。故选D。
27、100名村民选一名代表,候选人是甲、乙、丙三人,选举时每人只能投票选举一人,得票最多的人当选。开票中途累计,前61张选票中,甲得35票,乙得10票,丙得16票。在尚未统计的选票中,甲至少再得多少票就一定当选?_____
A: 11B: 12C: 13D: 14
参考答案: A 本题解释:正确答案是A考点趣味数学问题解析注意到在前61张票中,甲领先第二名丙35-16=19张。因此在剩下的100-61=39张票中,首先分配19张给乙,还剩20张。甲要保证一定当选,则应该获得剩余票量的过半数,也即11张。故正确答案为A。标签直接代入构造调整
28、卫育路小学图书馆一个书架分上、下两层,一共有245本书。上层每天借出15本,下层每天借出10本,3天后,上、下两层剩下图书的本数一样多。那么,上、下两层原来各有图书多少本?_____
A: 108,137B: 130,115C: 134,111D: 122,123
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析上层比下层多(15-10)×3=15本书,而两层共有245本书,故上层130本,下层115本。因此正确答案为B。
29、小王和小李6小时共打印了900页文件,小王比小李快50%。请问小王每小时打印多少页文件?_____
A: 60B: 70C: 80D: 90
参考答案: D 本题解释: 【解析】D。设小王每小时打印X页,因为小王比小李快50%,则小李每小时打印为X (1-50%)页,则根据题意可列:6X (1-50%)+6X=900,则X=90。
30、现有边长1米的一个木质正方体,已知将其放入水里,将有0.6米浸入水中。如果将其分割成边长0.25米的小正方体,并将所有的小正方体都放入水中,直接和水接触的表面积总量为_____。
A: 3.4平方米B: 9.6平方米C: 13.6平方米D: 16平方米
参考答案: C 本题解释:正确答案是C考点几何问题解析 秒杀技对大正方体,易得其浸在水中的面积为3.4平方米,恰为选项A。而分解过小正方体后总浸水面积比为比值的倍数。故正确答案为C。
秒杀技对大正方体,易得其浸在水中的面积为3.4平方米,恰为选项A。而分解过小正方体后总浸水面积比为比值的倍数。故正确答案为C。
31、已知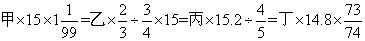 ,则甲、乙、丙、丁四个数中最大的是哪个?_____
,则甲、乙、丙、丁四个数中最大的是哪个?_____
A: 甲B: 乙C: 丙D: 丁
参考答案: B 本题解释:参考答案:B题目详解:原式化简为= ,乘以的数字越小,说明放大的倍数越小,则原数字越大。所以,选B考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
,乘以的数字越小,说明放大的倍数越小,则原数字越大。所以,选B考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
32、商店里有六箱货物,分别重15、16、18、19、20、31千克,两个顾客买走了其中五箱。已知一个顾客买的货物重量是另一个顾客的2倍。商店剩下的一箱货物重多少千克?_____。
A: 16 B: 18C: 19 D: 20
参考答案: D 本题解释:D 【解析】根据题意知道,货物的总重量是3个倍数,则它们的数字之和必定能被3整除,经过计算转换得知,剩下的那一箱重20千克。故选D。
33、甲、乙两地相距100千米,张先骑摩托车从甲出发,1小时后李驾驶汽车从甲出发,两人同时到达乙地。摩托车开始速度是50千米/小时,中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟,那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 1(1/2)C: 1/3D: 2
参考答案: C 本题解释: C 解析: 汽车行驶100千米需100÷80=1(1/4)(小时),所以摩托车行驶了1(1/4)+1+1/6=2(5/12)(小时)。如果摩托车一直以40千米/小时的速度行驶,2(5/12)小时可行驶9623千米,与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷(50-40)=1/3(小时)。故本题选C。
34、一个三位数,各位上的数的和是15,百位上的数与个位上的数的差是5,如颠倒各位上的数的顺序,则所成的新数比原数的3倍少39。求这个三位数。_____
A: 196B: 348C: 267D: 429
参考答案: C 本题解释:【解析】C。代入法。首先排除A和D;根据所成的新数比原数的3倍少39,用每个选项的最后一个数乘以3再减去,所得的数只有C中有。
35、某班学生不到50人,在一次考试中,有1/7人得优,1/3人得良,1/2人及格,其余的均不及格,那么不及格的人数是_____。
A: 1B: 2C: 3D: 4
参考答案: A 本题解释:正确答案是A考点倍数约数问题解析通过题干可知,该班级人数应为7、3、2的公倍数,又因为不能超过50人,所以该班人数为7×3×2=42人。那么不及格的人数为42-6-14-21=1。故正确答案为A。标签数字特性
36、一个空的容积为64 升的鼓形圆桶上有A、B 两孔,一种蒸馏水从A 孔流入同 时从B 孔流出,如果通过A 孔的流速为3 升/小时,那么在B 孔的流速为多少升时才能保证用96 小时恰好装满容器?_____
A: 4/3 B: 8/3 C: 7/3 D: 3/7
参考答案: C 本题解释:【答案】C[解析]从A孔流入同时从B孔流出,设流速X,则容器实际蓄水速度为3-X,所以64/(3-X)=96,求出X=7/3。
37、幼儿园里,老师将一堆桃子分给同学,如果每个同学分3个则余2个,如果每个同学分4个,则有两个同学分不到,该班有多少个同学?_____
A: 10B: 12C: 15D: 18
参考答案: A 本题解释:A【解析】设共有x个同学,由题意得3x+2=4(x-2),解得x=10。
38、五个人平均身高是169.4厘米,从矮到高排成一列,前三个人平均身高是166厘米,后三个人平均身高是172厘米,中间那个人身高是多少厘米?_____
A: 167B: 168C: 169D: 170
参考答案: A 本题解释:参考答案:A题目详解:中间那个人身高为:中间那个人的身高=前三个人的总身高+后三个人的总身高-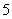 个人的身高;即
个人的身高;即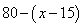 厘米;所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
厘米;所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
39、某个月有五个星期六,已知这五个日期的和为85,则这个月中最后一个星期六是多少号?_____
A: 10B: 17C: 24D: 31
参考答案: D 本题解释:【答案】D。解析:一个月有五个星期六,日期和为85,则平均数为17,因为五个星期六的日期构成公差为7的等差数列,平均数即是第三个星期六的日期,则第五个星期六的日期为17+7+7=31,故正确答案为D。
40、爷爷的老式时钟的时针与分针每隔66分重合一次。如果早晨8点将时钟对准,到第二天早晨时钟再次指示8点时,实际是几点几分?_____
A: 8点8分B: 8点10分C: 8点12分D: 8点16分
参考答案: C 本题解释:参考答案:C题目详解:对于标准钟表:时针与分针每重合一次需要 分;则老式时钟每重合一次比标准时间慢
分;则老式时钟每重合一次比标准时间慢 分;从12点开始的24时。分针转24圈,时针转2圈,分针比时针多转22圈,即22次追上时针;也就是说24时正好重合22次:所以老式时钟的时针与分针共重合了22次;所以比标准时间慢:
分;从12点开始的24时。分针转24圈,时针转2圈,分针比时针多转22圈,即22次追上时针;也就是说24时正好重合22次:所以老式时钟的时针与分针共重合了22次;所以比标准时间慢: 分;故实际时间为8点12分。所以,选C。考查点:数量关系>数学运算>特殊情境问题>钟表问题>时钟的校准问题
分;故实际时间为8点12分。所以,选C。考查点:数量关系>数学运算>特殊情境问题>钟表问题>时钟的校准问题
41、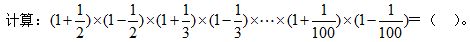 _____
_____
A: 101/100B: 101/200C: 101/300D: 201/400
参考答案: B 本题解释:正确答案是B考点计算问题解析 故正确答案为B。
故正确答案为B。
42、有一幢高楼,每上一层需2分钟,每下一层需1分30秒,某人于12点20分开始不停地从底层往上走,到了最高层后立即往下去(中途没有停留),13点零2分返回底层,则这幢楼一共有_____层。
A: 12B: 13C: 14D: 15
参考答案: B 本题解释:【解析】此人一共用了42分钟,上一层下一层共用2+1.5=3.5分钟,则这幢楼一共有42÷3.5+1=13层。
43、某公司举办年终晚宴,每桌安排7名普通员工与3名管理人员,到最后2桌时,由于管理人员已经安排完毕,便全部安排了普通员工,结果还是差2人才刚坐满,已经该公司普通员工数是管理人员的3倍,则该公司有管理人员_____名。
A: 24B: 27C: 33D: 36
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析设有管理人员的共有x桌,则管理人员共有3x人,从而普通员工共有9x人,则有9x=7x+18,解得x=9,所以管理人员共有27人。故正确答案为B。
44、用直线切割一个有限平面,后一条直线与此前每条直线都要产生新的交点,第1条直线将平面分成2块,第2条直线将平面分成4块。第3条直线将平面分成7块,按此规律将平面分为22块需_____。
A: 7条直线B: 8条直线C: 9条直线D: 6条直线
参考答案: D 本题解释:正确答案是D考点几何问题解析根据题意可知,设n为直线,S为分成的平面数,n=1时,S=2;n=2时,S=4;n=3时,S=7;n=4时,S=11;n=5时,S=16;n=6时,S=22。所以6条线可将平面分成22部分。故答案为D。
45、有一船从A城到B城,顺水时需要  小时,逆水时需要
小时,逆水时需要 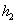 小时,如果两城之间距离是
小时,如果两城之间距离是 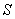 ,那么往返两城一次,平均速度为_____。
,那么往返两城一次,平均速度为_____。
A: 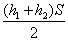 B:
B: 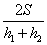 C:
C: 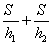 D:
D: 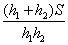
参考答案: B 本题解释:参考答案:.B题目详解:根据公式,可知:平均速度=总路程/总时间,总路程是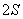 ,总时间是
,总时间是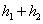 ,所以平均速度是
,所以平均速度是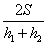 ;所以,选B。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
;所以,选B。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
46、如图,街道XYZ在Y处拐弯,XY=1125米,YZ=855米,在街道一侧等距装路灯,要求X,Y,Z处各装一盏路灯,这条街道最少要安装多少盏路灯?_____
A: 9月18日B: 10月14日C: 11月14日D: 12月18日
参考答案: C 本题解释:正确答案是C考点周期问题解析A、B、C、D四人的周期分别为6、12、18、30,因此周期的最小公倍数为180。从5月18日向后数180天,180天约为6个月,因此该时间必然落在11月,故正确答案为C。
47、南方某城市的一家企业有90%的员工是股民,80%的员工是“万元户”,60%的员工是打工仔,那么,这家企业的“万元户”中至少有多大比例是股民?_____
A: 67.5%B: 75%C: 87.5%D: 91.5%
参考答案: C 本题解释:C【解析】先假设这个企业共有员工100人,其中:90人是股民,即可知10人不是股民;80人是“万元户”,即可20人不是“万元户”;60人是打工仔。因此,“万元户”的80人至少有80-10=70人是股民,他们占全体“万元户”的70÷80×100%=87.5%。可见,本题正确答案为C。
48、一列快车和一列慢车相对而行,其中快车的车长200米,慢车的车长250米,坐在慢车上的旅客看到快车驶过其所在窗口的时间是6秒钟,坐在快车上的旅客看到慢车驶过其所在窗口的时间是多少秒钟?_____
A: 6秒钟B: 6.5秒钟C: 7秒钟D: 7.5秒钟
参考答案: D 本题解释:【答案解析】解析:追击问题的一种。坐在慢车看快车=>可以假定慢车不动,此时,快车相对速度为V(快)+V(慢),走的路程为快车车长200;同理坐在快车看慢车,走的距离为250,由于两者的相对速度相同=>250/x=200/6=>x=7.5(令x为需用时间)。
49、一个班的学生排队,如果排成3人一排的队列,则比2人一排的队列少8排;如果排成4人一排的队列,则比3人一排的队列少5排,这个班的学生如果按5人一排来排队的话,队列有多少排?_____
A: 9B: 10C: 11D: 12
参考答案: C 本题解释:正确答案是C考点不定方程问题解析注意到几人一排时,未必恰好整除,而在不整除的时候剩余人数仍构成一排,据此可知本题若列方程将不能得到一个确切方程,故解题方法为代入法。将A代入,则学生人数在41到45之间,择其最大者进行验证。45人满足排成3人一排的队列比排成2人一排的队列少8排,但排成4人一排的队列比3人一排的队列少3排,故45人不正确。并且此时排成4人一排的队列比3人一排的队列所少的排数低于题中给出的5,而要想排数差值增大,则需学生人数更多,因此41到45之间的数字肯定都不符合要求,故A不正确。(这也是为什么要择所得数字中最大者验证。)将B代入,则学生人数在46到50之间,择其最大者进行验证。学生人数为50人时,排成4人一排的队列比3人一排的队列少4排,故不符合,且类似上面分析可知B选项不正确。将C选项代入,则学生人数在51到55之间,择其最大者进行验证。学生人数为55人时,排成4人一排的队列比3人一排的队列少5排,符合要求,而其排成3人一排的队列比2人一排的队列少9排,因此学生人数应少于55人。依次验证其余可知学生人数为52人满足要求。故正确答案为C。
50、某工厂的一个生产小组,当每个工人都在岗位工作时,9小时可以完成一项生产任务。如果交换工人甲和乙的岗位,其他人不变,可提前1小时完成任务;如果交换工人丙和丁的岗位,其他人不变,也可提前1小时完成任务。如果同时交换甲和乙、丙和丁的岗位,其他人不变,可以提前多少小时完成这项任务?_____
A: 1.4B: 1.8C: 2.2D: 2.6
参考答案: B 本题解释:正确答案是B考点工程问题解析交换甲和乙或丙和丁的工作岗位,均可8小时完成任务,说明交换甲和乙或丙和丁,整体工作效率由1/9变为1/8,提高了1/72。则同时交换甲乙、丙丁,整体效率提高了1/36,则效率由1/9变成1/9+1/36=5/36,于是完成用时36/5=7.2(小时),提前了1.8小时完成。故正确答案为B。
51、从12时到13时,钟的时针与分针可成直角的机会有_____。
A: 1次B: 2次C: 3次D: 4次
参考答案: B 本题解释:【答案解析】一个小时内成直角只有两次,选B。
52、新年晚会上,老师让每位同学从一个装有许多玻璃球的口袋中摸两个球,这些球给人的手感相同,只有红、黄、白、蓝、绿五色之分,结果发现总有两个人取的球颜色相同。由此可知,参加取球的至少有_____人。
A: 13B: 14C: 15D: 16
参考答案: D 本题解释:【解析】摸出两个球,两球的颜色不同的情况有C25=10种,两个球的颜色相同的情况有5种,共有15种情况,所以至少有16人。
53、 _____
_____
A: 5B: 8C: 10D: 13
参考答案: C 本题解释:正确答案是C考点计算问题解析 标签尾数法
标签尾数法
54、有浓度为 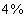 的盐水若干克,蒸发了一些水分后浓度变成
的盐水若干克,蒸发了一些水分后浓度变成 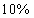 ,再加入300克
,再加入300克 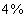 的盐水后.浓度变为
的盐水后.浓度变为 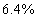 的盐水,问最初的盐水多少克?_____
的盐水,问最初的盐水多少克?_____
A: 200B: 300C: 400D: 500
参考答案: D 本题解释:参考答案 题目详解:解法一:应用十字交叉法:根据题意,设10%的盐水的质量为
题目详解:解法一:应用十字交叉法:根据题意,设10%的盐水的质量为 克,则有
克,则有 ,故有
,故有 ,解得
,解得 。则原有的盐水质量为
。则原有的盐水质量为 ,所以,选D。解法二:应用方程法:设最初的盐水为
,所以,选D。解法二:应用方程法:设最初的盐水为 克,300克4%的盐水含盐12克,则可以列方程为:
克,300克4%的盐水含盐12克,则可以列方程为: 其中:
其中: 为盐水混合后的盐含量;
为盐水混合后的盐含量; 为盐水混合后的盐水质量;解得,
为盐水混合后的盐水质量;解得, 克所以,选D。考查点:数量关系>数学运算>浓度问题>不同溶液混合
克所以,选D。考查点:数量关系>数学运算>浓度问题>不同溶液混合
55、某年级有84名学生,其中男生的年龄之和是女生的3倍。3年后,男生的年龄之和比女生年龄之和的3倍少36岁。问该年级男生有多少人?_____
A: 48B: 54C: 60D: 66
参考答案: C 本题解释:【答案解析】若男生人数为女生人数的3倍,则3年后,男生的年龄之和仍然为女生的3倍。3年后男生年龄之和比女生年龄之和的3倍少36岁,说明男生人数比女生人数的3倍少36÷3=12人,故女生人数为(84+12)÷(3+1)=24人,男生为84-24=60人。
56、市民广场中有两块草坪,其中一块草坪是正方形,面积为400平方米,另一块草坪是圆形,其直径比正方形边长长10%,圆形草坪的面积是多少平方米?_____
A: 410 B: 400 C: 390 D: 380
参考答案: D 本题解释: 【解析】正方形的边长是20米,那么圆的半径是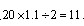 米,那么圆形草坪的面积是
米,那么圆形草坪的面积是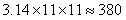 ,故选D。
,故选D。
57、某大型项目考察团队的所有员工年龄都在26~35岁之间,问:改考察团队至少有多少人才能保证在同一年出生的有5人?_____
A: 41B: 49C: 50D: 51
参考答案: A 本题解释:【答案】A。解析:最不利情况就是每年出生的人都有4个人,做题方法:最不利的情况数+1=4×10+1=41
58、一个自然数”x”,除以3的余数是2,除以4的余数是3,问”x”除以12的余数是_____。
A: 1B: 5C: 9D: 11
参考答案: D 本题解释:正确答案是D考点计算问题解析直接代入选项,很明显只有D符合,故正确答案为D。标签直接代入
59、一排长椅共有90个座位。其中一些座位已经有人就座了。这时,又来了一个人要坐在这排长椅上,有趣的是,他无论坐在哪个座位上都与已经就座的某个人相邻。原来至少有多少人已经就座?_____
A: 3lB: 30C: 29D: 32
参考答案: B 本题解释:参考答案:B题目详解:解法一:根据题意:可推知这排长椅上已经就座的任意相邻的两人之间都有两个空位;已经就座的人最左边一个(最右边一个)既可以坐在左边…边)起第一个座位上,也可以坐在左边(右边)起第二个座位上(如图所排…的两种情况,“●”表示已经就座的人,“○”表示空位)。(1)●○○●○○●…(2)○●○○●○○●○……题目中问“至少”有多少人就座:那就应选第二种情况,每三人(○●○)一组,所以共有 人。所以,选B。解法二:已经就坐的人占据的座位应该为第2,5,8.....:组成一个公差为3等差数列;即第
人。所以,选B。解法二:已经就坐的人占据的座位应该为第2,5,8.....:组成一个公差为3等差数列;即第 个人占据第
个人占据第 个座位时新来的人无论坐哪个座位上都与已经就坐的某个人相邻且
个座位时新来的人无论坐哪个座位上都与已经就坐的某个人相邻且 因为人数只能取整数所以
因为人数只能取整数所以 最大取30;所以,选B。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
最大取30;所以,选B。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
60、一篇文章,现有甲、乙、丙三人,如果由甲、乙两人合作翻译,需要10小时完成,如果由乙、丙两人合作翻译,需要12小时完成。现在先由甲、丙两人合作翻译4小时,剩下的再由乙单独去翻译,需要12小时才能完成,则,这篇文章如果全部由乙单独翻译,要多少个小时完成?_____
A: 15B: 18C: 20D: 25
参考答案: A 本题解释:正确答案是A考点工程问题解析设总量为1,由题意知甲乙合作的效率为1/10,乙丙合作的效率为1/12。题目给出完成该项工程的过程是甲丙先合作4个小时,乙单独翻译12个小时。在这个工作过程中,甲完成了4个小时的工作量,已完成了12个小时的工作量,丙完成了4个小时的工作量,保持此总量不变,将乙的工作拆分为三个独立的4个小时,重新为如下工作过程:甲乙先合作4个小时,乙丙再合作4个小时,最后乙单独做4个小时,仍然可以保证工程完成。于是假设乙的效率为y,可知4×1/10+4×1/12+4y=1,解得y=1/15,于是乙单独完成需要15个小时,故正确答案为A。
61、某工厂原来每天生产100个零件,现在工厂要在12天内生产一批零件,只有每天多生产10%才能按时完成工作,第一天和第二天由于部分工人缺勤,每天只生产了100个,那么以后10天平均每天要多生产百分之几才能按时完成工作?_____
A: 12%B: 13%C: 14%D: 15%
参考答案: A 本题解释:正确答案是A考点工程问题解析每天需要多生产10%,共生产12天;由于工人缺勤,前两天为原产量,故12天多生产的量需要10天完成,则每天多生产10%×12÷10=12%。故正确答案为A。
62、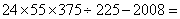 _____
_____
A: 168B: 172C: 184D: 192
参考答案: D 本题解释:参考答案 题目详解:<暂无>考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
题目详解:<暂无>考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
63、某公司要在长、宽、高分别为50米、40米、30米的长方体建筑的表面架设专用电路管道联接建筑物内最远两点,预设的最短管道长度介于_____。
A: 70—80米之间B: 60—70米之间C: 90—100米之间D: 80—90米之间
参考答案: D 本题解释:正确答案是D考点几何问题解析
64、商店里有六箱货物,分别重15、16、18、19、20、31千克,两个顾客买走了其中五箱,已知一个顾客买的货物重量是另一个顾客的2倍。商店剩下的一箱货物重多少千克_____
A: 16B: 18C: 19D: 20
参考答案: D 本题解释: 【解析】D。由题可知卖出的五箱货物一定能被3整除,六箱货物的总重为119千克,只有D项能使五箱货物被3整除,故选D。
65、(2008广东,第11题)某人工作-年的报酬是18000元和-台洗衣机,他干了7个月不干了,得到9500元和-台洗衣机,这台洗衣机价值多少钱?_____
A: 8500B: 2400C: 2000D: 1500
参考答案: B 本题解释:参考答案:B题目详解:根据题意,假设这个人一个月的报酬为 元,洗衣机价值为
元,洗衣机价值为 元,则:
元,则: 所以,选B。考查点:数量关系>数学运算>利润利率问题>其他利润相关问题
所以,选B。考查点:数量关系>数学运算>利润利率问题>其他利润相关问题
66、解放军某部有600人,他们排成四路纵队,每相邻两排之间前后相距1米。队伍每分钟行75米,现在要通过一座长676米的桥,从排头上桥到排尾离桥共需多少分钟?_____
A: 10B: 11C: 12D: 13
参考答案: B 本题解释:参考答案:B题目详解:四路纵队,就是600人排成4路(列):即每列150人;每相邻两排之间前后相距1米:150人有149个间隔,则队列长为149米;依题意:队伍长为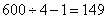 米,通过桥需
米,通过桥需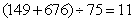 分钟。所以,选B。考查点:数量关系>数学运算>行程问题>初等行程问题
分钟。所以,选B。考查点:数量关系>数学运算>行程问题>初等行程问题
67、某办公室共有7个科员,2个副主任,现安排1个副主任带4个科员作出考察,不同的安排方案共有_____。
A: 70种B: 210种C: 212种D: 420种
参考答案: A 本题解释:正确答案是A考点排列组合问题解析
68、某商店花10000元进了一批商品,按期望获得相当于进价25%的利润来定价,结果只销售了商品总量的30%,为尽快完成资金周转,商店决定打折销售,这样卖完全部商品后,亏本1000元,问商店是按定价打几折销售的?_____
A: 九折B: 七五折C: 六折D: 四八折
参考答案: C 本题解释:正确答案是C考点经济利润问题解析解析1:某商品进该批产品成本为10000元,其中30%是按照相当于进价25%的利润定价,也即3000元的部分是按此利润售出的,此部分回收资金为3000×1.25=3750(元)。根据亏本1000元,可知总共收回资金为9000元,因此剩下的7000元商品实际只售出9000-3750=5250(元),故折扣为5250÷(7000×1.25)=0.6,也即6折。故正确答案为C。解析2:设一共有10件商品,折扣为Y,则每件商品进价为1000元,利润为250元,可列方程1250×3+1250Y×7=9000,解得Y=0.6,故正确答案为C。标签赋值思想
69、9e2006的个位数是_____。(9e2006表示9的2006次方)
A: 1B: 2C: 8D: 9
参考答案: A 本题解释:正确答案是A考点计算问题解析9的奇数次方尾数为9,偶数次方尾数为1,故9e2006的为数尾数为1,正确答案为A。
70、某市居民生活用电每月标准用电量的基本价格为每度0.60元,若每月用电量超过标准用电量,超出部分按基本价格的80%收费,某户九月份用电100度,共交电费57.6元,则该市每月标准用电量为_____。
A: 60度B: 70度C: 80度D: 90度
参考答案: C 本题解释:正确答案是C考点分段计算问题解析设该市每月标准用电量为a度,则可列方程a×0.6+(100-a)×0.6×0.8=57.6,则a=80(度),故正确答案为C。
71、2004×(2.3×47+2.4)÷(2.4×47-2.3)的值为_____。
A: 2003B: 2004C: 2005D: 2006
参考答案: B 本题解释:正确答案是B考点计算问题解析原式=2004×(2.3×47+2.4)÷[(2.3+0.1)×47-2.3]=2004×(2.3×47+2.4)÷(2.3×47+4.7-2.3)=2004×(2.3×47+2.4)÷(2.3×47+2.4)=2004。因此正确答案为B。
72、某企业组织80名员工一起去划船,每条船乘客定员12人,则该企业最少需要租船_____条。
A: 7B: 8C: 9D: 10
参考答案: A 本题解释:正确答案是A考点趣味数学问题解析80÷12=6……8,6条船不够,至少7条。故正确答案为A。
73、小陈家住在5楼,他每天上下楼各一次,共需走120级楼梯。后来小陈家搬到同一栋楼的8楼,如果每层楼的楼梯级数相同,则他搬家后每天上下楼一次共需走楼梯_____级。
A: 168B: 192C: 210D: 240
参考答案: C 本题解释:正确答案是C考点计数模型问题解析住在5楼,需要走5-1=4层楼梯,住在8楼,修要走8-1=7层楼梯,每层楼梯级数不变,则可得120÷4×7=210级。故正确答案为C。
74、有3个企业共订阅300份《经济周刊》杂志,每个企业最少订99份,最多订101份,问一共有多少种不同的订法?_____
A: 6B: 7C: 8D: 9
参考答案: B 本题解释:正确答案是B考点排列组合问题解析 故正确答案为B。
故正确答案为B。
75、甲从某地出发均速前进,一段时间后,乙从同一地点以同样的速度同向前进,在K时刻乙距起点30米;他们继续前进,当乙走到甲在K时刻的位置时,甲离起点108米。问:此时乙离起点多少米?_____
A: 39米B: 69米C: 78米D: 138米
参考答案: B 本题解释:正确答案是B考点行程问题解析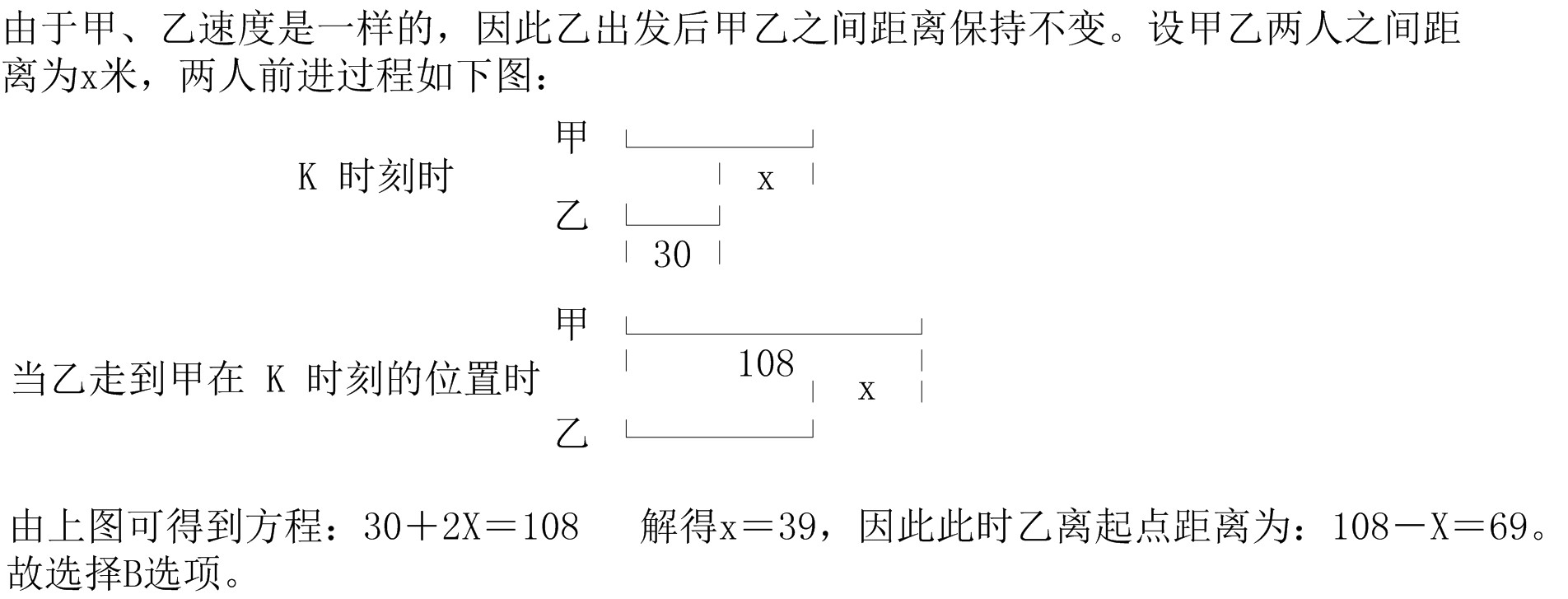
76、松鼠妈妈采松果,晴天每天可采20个,雨天每天只能采12个。它一连几天共采了112个松果,平均每天采14个。这几天中有几天下雨?_____
A: 3B: 4C: 5D: 6
参考答案: D 本题解释:【答案解析】松鼠妈妈一连采了松果的天数为:112÷14=8(天)。设雨天有x天,则晴天有(8-x)天,列方程得20×(8-x)+12x=1125×(8-x)+3x=28x=6故本题正确答案为D。
77、在20件产品中,有15件一级品,5件二级品,从中任取3件,其中至少有一件为二级品的概率是多少?_____
A: 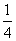 B:
B: 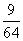 C:
C: 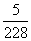 D:
D: 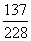
参考答案: D 本题解释:参考答案 题目详解:在20件产品中任取3件:可以有
题目详解:在20件产品中任取3件:可以有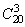 种情况;3件都是一级品的情况为:有
种情况;3件都是一级品的情况为:有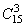 种情况;因此至少有一件为二级品的情况:有
种情况;因此至少有一件为二级品的情况:有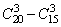 种情况;因此至少有一件为二级品的概率是:
种情况;因此至少有一件为二级品的概率是: ;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
78、某机关单位召开一次会议预期12天,后因会期缩短4天,因此原预算费用节约了一部分。其中生活费一项节约了4000 ,比原计划少用40%,生活费预算占总预算的4/9,则总预算为_____。
A: 45000元:B: 35000元C: 27500元D: 22500元
参考答案: D 本题解释:D【精析】生活费比计划少用40%,因此计划中的生活费为4000÷40%=10000元。该项费用占总预算的9/4因此总预算为10000×9/4=22500元。
79、一个学雷锋小组的大学生们每天到餐馆打工半小时,每人可挣3元钱。到11月11日,他们一共挣了1764元。这个小组计划到12月9日这天挣足3000元捐给“希望工程”。因此小组必须在几天后增加一个人。增加的这个人应该从11月_____日起每天到餐馆打工,才能到12月9日恰好挣足3000元钱。
A: 18B: 24C: 14D: 20
参考答案: D 本题解释:D[解析]还缺3000-1764=1236(元),从11月12日~12月9日还有30+9-12+1=28(天),这28天中,(原来小组中)每人可挣3×28=84(元)。因为1236÷84=14……60,所以原有14人,必须增加一个人挣60元。60÷3=20(天),30+9-20+1=20,所以增加的这个人应该从11月20日起去打工。
80、(2008安徽,第15题)某企业有甲、乙、丙三个仓库,且都在一条直线上,之间分别相距l千米、3千米,三个仓库里面分别存放货物5吨、4吨、2吨。如果把所有的货物集中到一个仓库,每吨货物每千米运费是90元,请问把货物放在哪个仓库最省钱?_____
A: 甲B: 乙C: 丙D: 甲或乙
参考答案: B 本题解释:参考答案:B题目详解:此题遵循“小往大处靠”原则,先把2吨的货物移动到4吨那,这样就相当于有了6吨货物,然后在把5吨的货物也移动到6吨,综上所述,运到乙仓库最省钱考查点:数量关系>数学运算>统筹问题>货物集中问题
81、在一次国际美食大赛中,中、法、日、俄四国的评委对一道菜品进行打分。中国评委和法国评委给出的平均分是94,法国评委和日本评委给出的平均分是90,日本评委和俄罗斯评委给出的平均分是92,那么中国评委和俄罗斯评委给出的平均分是_____。
A: 93分B: 94分C: 96分D: 98分
参考答案: C 本题解释:C【解析】设中、法、日、俄四国的评委给出的分数分别是A、B、C、D,根据题意可知:A+B=94×2,B+C=90×2,C+D=92×2,又因为A+D=(A+B)+(C+D)-(B+C)=94×2+92×2-90×2=(94+92-90)×2=96×2所以中国评委和俄国评委给出的平均分是96分,本题正确答案为C。
82、在400米环形跑道上,A、B两点相距100米。甲、乙两人分别从A、B两点同时出发,按逆时针方向跑步。甲每秒跑5米,乙每秒跑4米。每人每跑100米,都要停10秒。那么,甲追上乙需要的时间是_____秒。
A: 80B: 100C: 120D: 140
参考答案: D 本题解释:【答案解析】假设甲、乙都不停地跑,那么甲追上乙的时间是100÷(5-4)=100(秒)。甲、乙每跑100米停10秒,等于甲跑20秒(100÷5)休息10秒,乙跑25秒(100÷4)休息10秒。跑100秒甲要停4次(100÷20-1),共用140秒(100+10×4),此时甲已跑的路程为500米。在第130秒时乙已跑路程为400米(他此时已休息3次,花去30秒),并在该处休息到第140秒,甲刚好在乙准备动身时赶到,他们碰到一块了。所以,甲追上乙需要的时间是140秒。故选D。
83、有面值为8分、1角和2角的三种纪念邮票若干张,总价值为1元2角2分,则邮票至少有_____。
A: 7张B: 8张C: 9张D: 10张
参考答案: C 本题解释:C【解析】要使邮票最少,则要尽量多的使用大面额邮票,所以要达到总价值,2角的邮票要使用4张,1角的邮票要使用1张,8分的邮票要4张,这样使总价值正好为1元2角2分,所以要用9张。
84、
85、A大学的小李和B大学的小孙分别从自己学校同时出发,不断往返于A、B两校之间。现已知小李的速度为85米/分,小孙的速度为105米/分,且经过12分钟后两人第二次相遇。问A,B两校相距多少米?_____
A: 1140米B: 980米C: 840米D: 760米
参考答案: D 本题解释:易知到第二次相遇时,两人合起来走过的距离恰为A、B两校距离的3倍,因此A、B两校相距(85+105)×12÷3=760(米)。故选D。
86、王家村西瓜大丰收后,全村男女老少分四个组品尝西瓜,且每组人正好一样,小伙子一个人吃1个,姑娘两个人吃1个,老人三个人吃1个,小孩四个人吃1个,一共吃了200个西瓜,问王家村品尝西瓜的共有_____
A: 368人B: 384人C: 392人D: 412人
参考答案: B 本题解释: B。方法一:利用整除关系。答案必须是2,3,4的公倍挚,也就是说答案必须是12的整数倍数。只有B满足。方法二:假设每组有x人。x+x/2+x/3+x/4=200,解得x=96,96×4=384(人)。
87、电影票10元一张,降价后观众增加一倍,收入增加1/5,则一张票降价多少元?_____
A: 8B: 6C: 4D: 2
参考答案: C 本题解释:答案:C。代入法。10元一张票,一个人去看,总收入10元,降价了以后, 观众增加了1倍,2个人去看,收入增加了1/5,也就是说,两个人看收入为12元,每张票价就是6元钱,相比原来的10元钱一张,下降了4元,所以答案是C
88、有一种红砖,长24厘米、宽12厘米、高5厘米,问至少用多少块这种砖才能拼成一个实心的正方体?_____
A: 600块B: 1200块C: 1800块D: 2400块
参考答案: B 本题解释:B。
89、 _____
_____
A: 1B: 1/2007C: 2007D: 1/1035
参考答案: B 本题解释:正确答案是B考点数列问题解析
90、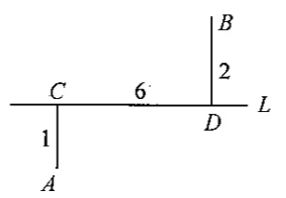
A: 2.75B: 3.25C: 2D: 3
参考答案: 本题解释:参考答案:C题目详解:由两点之间线段最短可知:连接AB,交公路L于点E,E点就是A、B两个村庄到此处处理垃圾都比较方便的地方。设CE距离为x:根据tanA=a/b可得:tanA=x/1=x,tanB=(6-x)/2=3-x/2;由于∠A=∠B:故x=3-x/2,解得,x=2。即应建在离C处2公里。所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>与线、角相关问题(平面)
91、某单位职工24人中,有女性11人,已婚的有16人。在已婚的16人中有女性6人。问这个单位的未婚男性有多少人?_____
A: 1B: 3C: 9D: 12
参考答案: B 本题解释:正确答案是B考点容斥原理问题解析由题意:未婚共有:24-16=8人,其中未婚女性有:11-6=5人,故未婚男性有:8-5=3人。
92、完成某项工程,甲单独工作需要18小时,乙需要24小时,丙需要30小时。现按甲、乙、丙的顺序轮班工作,每人工作一小时换班。当工程完工时,乙总共干了多少小时?_____
A: 8小时B: 7小时44分C: 7小时D: 6小时48分
参考答案: B 本题解释:正确答案是B考点工程问题解析解析1:设工程总量为360,则甲乙丙的工作效率分别为20、15、12,三人每小时工作总量为47。由题意可知三人轮班即为循环周期问题,用360除以47商7余数为31,甲乙丙轮班每人7小时后,乙继续工作的工作量为31-20=11。所以最终乙总共干了:7小时+11/15×60分=7小时44分,故正确答案为B。解析2:设工程总量为360,则甲乙丙的工作效率分别为20、15、12,甲每小时比乙多干5,乙每小时比丙多干3,因此乙工作时间必定小于24/3=8小时。观察选项有6小时、7小时和8小时,可选7为参考点,甲乙丙轮班每人工作7小时共完成:(20+15+12)×7=329<360,因此乙工作时间在7小时和8小时之间,故正确答案为B。标签赋值思想
93、有100人参加运动会的三个比赛项目,每人至少参加一项,其中未参加跳远的有50人,未参加跳高的有60人,未参加赛跑的有70人。问至少有多少人参加了不止一个项目?_____
A: 7B: 10C: 15D: 20
参考答案: B 本题解释:【解析】B。最值问题。由题意,参加跳远的人数为50人,参加跳高的为40人,参加赛跑的为30人;即参加项目的人次为120人次;故欲使参加不止一项的人数最少,则需要使只参加一项的人数最多为x,参加3项的人数为y;故x+3y=120,x+y=100,解得y=10。
94、A、B两地相距320千米,甲、乙二人驾车分别从A、B两地相向而行,甲每小时行36千米,乙每小时比甲多行8千米。甲、乙各有一部对讲机,对讲机的使用范围是40千米。那么,甲、乙二人出发后(B)小时可以开始用对讲机联络。A.35/8B.3.5C.17/4D.4.5
A: 35/8B: 3.5C: 17/4D: 4.5
参考答案: B 本题解释:B【解析】当对讲机可以使用时,甲、乙二人共行驶了320-40=280(千米)。设出发后t小时可以开始用对讲机联络,根据题意可得方程:36t+(36+8)t=280,解得t=3.5(小时),由此可知本题答案为B。
95、有8个队参加比赛,采用所示的淘汰制方式。问在比赛前抽签时,可以得到多少种实质不同的比赛安排表?_____ 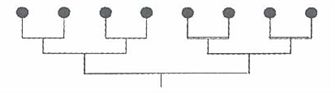
A: 4030B: 315C: 5040D: 164
参考答案: B 本题解释:参考答案:B题目详解:我们标上字母如图:全排列为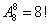 。因为A/B,B/A实质赛程一样;同理:C/D,E/F,G/H,I/J,K/L,M/N均是,所以除以7个2。于是,共有
。因为A/B,B/A实质赛程一样;同理:C/D,E/F,G/H,I/J,K/L,M/N均是,所以除以7个2。于是,共有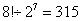 种实质不同的赛程安排。所以,选B。
种实质不同的赛程安排。所以,选B。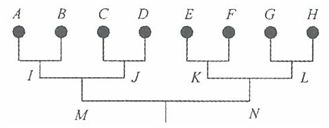 考查点:数量关系>数学运算>排列组合问题>比赛问题>淘汰赛
考查点:数量关系>数学运算>排列组合问题>比赛问题>淘汰赛
96、(2006江苏)甲、乙、丙三人进行百米赛跑,甲到终点时,乙离终点2米,丙离终点3米。在各自速度不变的情况下,乙到终点时,丙离终点还有多少米?_____
A: 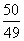 B:
B: 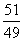 C:
C: 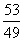 D: 1
D: 1
参考答案: A 本题解释:参考答案A题目详解:设乙到终点时,丙已经跑了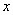 米。根据条件,时间相同,速度与距离成正比:
米。根据条件,时间相同,速度与距离成正比: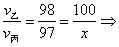
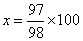 ,丙距终点
,丙距终点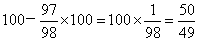 米。考查点:数量关系>数学运算>行程问题>追及问题>直线追及问题>直线一次追及问题
米。考查点:数量关系>数学运算>行程问题>追及问题>直线追及问题>直线一次追及问题
97、(2006国家,第49题)某原料供应商对购买其原料的顾客实行如下优惠措施:①-次购买金额不超过1万元,不予优惠; ②-次购买金额超过1万元,但不超过3万元,给九折优惠; ③-次购买金额超过3万元,其中3万元九折优惠,超过3万元部分八折优惠。某厂因库容原因,第-次在该供应商处购买原料付款7800元,第二次购买付款26100元,如果他-次购买同样数量的原料,来源:91考试网 www.91eXam.org可以少付多少元?_____
A: 1460元B: 1540元C: 3780元D: 4360元
参考答案: A 本题解释:参考答案:A题目详解:第-次付款7800元,因此第-次购买的原料价值7800元(不打折);第二次付款26100元,因此第二次购买的原料价值 元(打九折);所以两次购买的原料总价值为
元(打九折);所以两次购买的原料总价值为 元。①
元。① 的部分,应付
的部分,应付 元;②
元;② 元的部分,应付
元的部分,应付 元。综上,总共少支付
元。综上,总共少支付 元。考查点:数量关系>数学运算>统筹问题>最优效率分配问题
元。考查点:数量关系>数学运算>统筹问题>最优效率分配问题
98、用红、黄两色鲜花组成的实心方阵(所有花盆大小完全相同),最外层是红花,从外往内每层按红花、黄花相间摆放。如果最外一圈的正方形有红花44盆,那么完成造型共需黄花_____。
A: 48盆B: 60盆C: 72盆D: 84盆
参考答案: B 本题解释:正确答案是B考点计数模型问题解析最外层有红花44盆,则边长为44÷4+1=12盆,因此黄花的第一圈边长为10盆,依次向内为6盆、2盆,共计3圈。各圈黄花盆数成等差数列,依次为36盆、20盆、4盆,故共需黄花60盆。故正确答案为B。
99、某日小李发现日历有好几天没有翻,就一次翻了6张,这6天的日期加起来的数字和是141,他翻的第一页是几号?_____
A: 18 B: 21 C: 23 D: 24
参考答案: B 本题解释: 【解析】B。设第一张的日期为X,则可得方程X+X+1+X+2+X+3+X+4+X+5=141,解得X=21,所以选答案B。
100、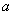 除以5余1,
除以5余1,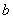 除以5余4,如果
除以5余4,如果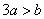 ,那么
,那么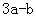 除以5余几?_____
除以5余几?_____
A: 1B: 2C: 3D: 4
参考答案: D 本题解释:参考答案 题目详解:
题目详解: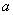 除以5余1,
除以5余1,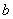 除以5余4设
除以5余4设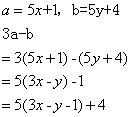 非负整数
非负整数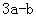 除以5的余数4(该解析由用户“shery”于2010-10-1516:40:16贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之数的性质>余数问题>多个被除数,一个除数>不同余
除以5的余数4(该解析由用户“shery”于2010-10-1516:40:16贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之数的性质>余数问题>多个被除数,一个除数>不同余