时间:2013-01-08 07:45:42
数学二试题答案
一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1)(C)
(2)(C)
(3)(C)
(4)(D)
(5)(A)
(6)(B)
(7)(B)
(8)(B)
二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(9)答案:![]()
(10)答案:![]()
(11)答案:![]()
(12)答案:![]()
(13)答案:![]()
(14)答案:![]()
三、解答题:15—23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)解析:因为当![]() 时,
时,![]() 与
与![]() 为等价无穷小
为等价无穷小
所以![]()
又因为:
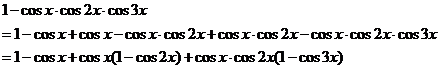
即![]()
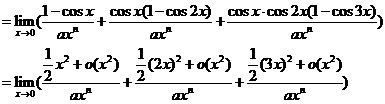
所以![]() 且
且![]()
(16)解析:由题意可得:
![]()
![]()
因为:![]() 所以
所以![]()
(17)解析:![]()
![]()
![]()
(18)解析:(1)令![]()
则![]() 使得
使得![]()
(2)令![]() 则
则![]()
又由于![]() 为奇函数,故
为奇函数,故![]() 为偶函数,可知
为偶函数,可知![]() ,
,
则![]() 使
使![]()
即![]() ,即
,即![]()
(19)最长![]() ,最短
,最短![]()
(20)答案:(1)、![]()
(2)、由于![]() ,则
,则![]() ,即
,即![]() ,故
,故![]() 单调递增。
单调递增。
又由于![]() ,则
,则![]() ,故
,故![]() 有上界,则由单调有界收敛定理可知,
有上界,则由单调有界收敛定理可知,![]() 存在。令
存在。令![]() ,则
,则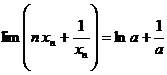 ,由于
,由于![]() ,则
,则
![]() ,故
,故![]() 。
。
(21)答案:(1)、![]()
(2)、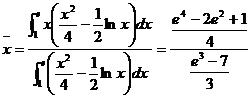
(22)答案:
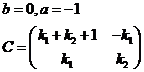
(23)答案:(1)
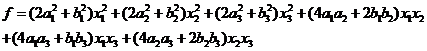
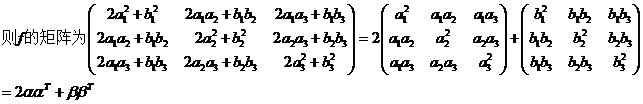 (2)
(2)![]() ,则1,2均为A的特征值,又由于
,则1,2均为A的特征值,又由于![]() ,故0为A的特征值,则三阶矩阵A的特征值为2,1,0,故f在正交变换下的标准形为
,故0为A的特征值,则三阶矩阵A的特征值为2,1,0,故f在正交变换下的标准形为
" >